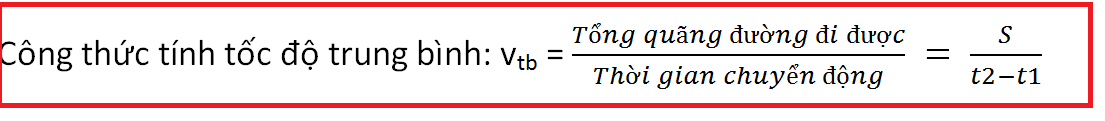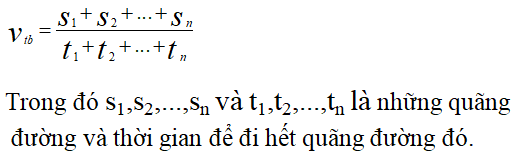Vận tốc trung bình có âm không? Khám phá khái niệm và ứng dụng thực tế

Vận tốc trung bình có thể nhận giá trị âm, phụ thuộc vào hướng di chuyển của vật thể. Trong vật lý, vận tốc trung bình là một đại lượng vectơ, nghĩa là nó không chỉ có độ lớn mà còn có hướng. Để xác định vận tốc trung bình, ta sử dụng công thức:

\[
v_{tb} = \frac{\Delta x}{\Delta t}
\]

Trong đó:

• \(v_{tb}\): Vận tốc trung bình
• \(\Delta x\): Độ dịch chuyển (có thể âm hoặc dương)
• \(\Delta t\): Thời gian di chuyển (luôn dương)

Vận tốc trung bình sẽ có giá trị âm khi độ dịch chuyển của vật thể là âm, nghĩa là vật thể di chuyển ngược lại so với hướng quy ước ban đầu. Ví dụ, nếu quy ước di chuyển về phía đông là dương, thì di chuyển về phía tây sẽ là âm, do đó vận tốc trung bình cũng sẽ âm.

Ví dụ minh họa:

Giả sử một chiếc xe di chuyển từ điểm A đến điểm B, sau đó quay ngược lại về điểm C (nằm giữa A và B). Nếu quy ước di chuyển từ A đến B là hướng dương, thì khi xe quay lại về phía C, độ dịch chuyển sẽ là âm, dẫn đến vận tốc trung bình có thể âm.

Tính chất của vận tốc trung bình:

• Vận tốc trung bình phụ thuộc vào độ dịch chuyển, không phải tổng quãng đường.
• Vận tốc trung bình có thể âm khi vật thể di chuyển ngược hướng so với hướng quy ước dương.
• Độ lớn của vận tốc trung bình luôn là giá trị dương.

Ví dụ, nếu một người đi 10 mét về phía đông (hướng dương), sau đó quay lại đi 5 mét về phía tây (hướng âm), vận tốc trung bình sẽ được tính dựa trên độ dịch chuyển tổng cộng là 5 mét theo hướng đông (dương).

Vận tốc trung bình là một khái niệm cơ bản trong vật lý, được định nghĩa là tỉ số giữa quãng đường mà một vật di chuyển và thời gian mà vật đó thực hiện quãng đường đó. Công thức tính vận tốc trung bình là:

\[
v_{\text{tb}} = \frac{\Delta s}{\Delta t}
\]

Trong đó:

• \(\Delta s\): Quãng đường di chuyển
• \(\Delta t\): Thời gian di chuyển

Vận tốc trung bình có thể có giá trị dương hoặc âm tùy thuộc vào chiều di chuyển của vật so với hệ quy chiếu. Nếu vật di chuyển theo chiều dương của trục tọa độ, vận tốc trung bình sẽ dương. Ngược lại, nếu vật di chuyển theo chiều âm của trục, vận tốc trung bình sẽ âm.

Một điểm quan trọng cần lưu ý là vận tốc trung bình chỉ thể hiện tốc độ và hướng di chuyển trung bình trong một khoảng thời gian nhất định, không phản ánh sự thay đổi tốc độ tức thời của vật tại các thời điểm khác nhau.

Khái niệm này không chỉ áp dụng trong các bài toán lý thuyết mà còn có ý nghĩa quan trọng trong đời sống hàng ngày như tính toán tốc độ trung bình của xe cộ, quá trình sản xuất, hay các hoạt động thể thao.

Vận tốc trung bình của một vật thể không chỉ phụ thuộc vào khoảng cách đã di chuyển mà còn chịu tác động từ nhiều yếu tố khác nhau. Hiểu rõ các yếu tố này giúp chúng ta dự đoán và điều chỉnh vận tốc trung bình trong các tình huống thực tế. Dưới đây là những yếu tố chính ảnh hưởng đến vận tốc trung bình:

• Quãng đường di chuyển: Tổng quãng đường mà vật thể di chuyển càng dài thì thời gian di chuyển càng tăng, từ đó ảnh hưởng đến vận tốc trung bình.
• Thời gian di chuyển: Thời gian cần thiết để hoàn thành quãng đường cũng là một yếu tố quyết định. Nếu thời gian di chuyển giảm, vận tốc trung bình sẽ tăng và ngược lại.
• Điều kiện di chuyển: Các yếu tố bên ngoài như thời tiết, tình trạng giao thông, và địa hình có thể làm tăng hoặc giảm thời gian di chuyển, qua đó ảnh hưởng đến vận tốc trung bình.
• Sự thay đổi tốc độ: Nếu tốc độ của vật thể thay đổi trong suốt quá trình di chuyển, điều này cũng sẽ ảnh hưởng đến vận tốc trung bình cuối cùng.

Những yếu tố này đều có ảnh hưởng nhất định đến việc tính toán vận tốc trung bình, và việc hiểu rõ chúng giúp bạn dự đoán kết quả chính xác hơn trong thực tế.

Vận tốc trung bình là một khái niệm cơ bản nhưng có nhiều ứng dụng quan trọng trong đời sống hàng ngày và các ngành công nghiệp. Việc sử dụng vận tốc trung bình không chỉ giúp tính toán thời gian di chuyển mà còn cải thiện hiệu suất trong nhiều lĩnh vực khác nhau.

• Giao thông và vận tải: Trong ngành giao thông, vận tốc trung bình được sử dụng để lập kế hoạch hành trình, ước tính thời gian đến nơi, và điều chỉnh tốc độ di chuyển nhằm tiết kiệm nhiên liệu và đảm bảo an toàn. Ví dụ, các hệ thống định vị GPS thường dựa trên vận tốc trung bình để cung cấp thông tin chính xác về thời gian dự kiến đến nơi.
• Thể thao: Trong các môn thể thao như điền kinh và đua xe, vận tốc trung bình được sử dụng để đánh giá hiệu suất của các vận động viên. Việc theo dõi vận tốc trung bình có thể giúp các huấn luyện viên điều chỉnh chiến thuật và nâng cao thành tích.
• Khoa học và kỹ thuật: Vận tốc trung bình là một công cụ quan trọng trong nghiên cứu chuyển động của các thiên thể, cũng như trong việc phân tích dòng chảy của chất lỏng và khí. Điều này giúp các nhà khoa học dự đoán các hiện tượng tự nhiên và cải tiến công nghệ.
• Ứng dụng trong công nghiệp: Vận tốc trung bình cũng được sử dụng để đo lường và kiểm soát dòng chất lỏng trong các hệ thống sản xuất. Nhờ đó, có thể cải thiện hiệu quả sản xuất, giảm thiểu lãng phí và tối ưu hóa quy trình.
• Giáo dục: Trong các lớp học vật lý, vận tốc trung bình được sử dụng như một khái niệm cơ bản để giảng dạy về các định luật chuyển động. Học sinh có thể áp dụng các kiến thức này vào thực tế, giúp nâng cao hiểu biết về khoa học tự nhiên.

Vận tốc trung bình thường được hiểu là một đại lượng dương, vì nó mô tả quãng đường di chuyển của một vật thể trong một khoảng thời gian nhất định. Tuy nhiên, câu hỏi liệu vận tốc trung bình có thể âm hay không cần được phân tích kỹ càng từ góc độ vật lý và toán học.

Khi xem xét khái niệm này, ta cần hiểu rằng vận tốc trung bình \(\overline{v}\) được tính bằng công thức:

Trong đó, \(\Delta x\) là độ dời của vật thể và \(\Delta t\) là thời gian di chuyển. Độ dời là khoảng cách từ vị trí ban đầu đến vị trí cuối cùng của vật thể, và nó có thể mang giá trị âm nếu vật thể di chuyển theo hướng ngược lại với chiều dương đã quy ước.

• Vận tốc trung bình âm: Trong trường hợp độ dời \(\Delta x\) âm, nghĩa là vật thể di chuyển ngược chiều với hướng đã chọn là dương, vận tốc trung bình sẽ có giá trị âm. Ví dụ, nếu bạn đi ngược lại từ điểm cuối về điểm đầu, độ dời sẽ là âm và vận tốc trung bình sẽ âm.
• Ý nghĩa vật lý: Vận tốc trung bình âm không có nghĩa là vật thể di chuyển chậm hơn, mà chỉ ra hướng di chuyển của vật thể là ngược lại với chiều dương đã chọn. Điều này có thể xảy ra trong nhiều trường hợp, chẳng hạn như trong chuyển động tròn hoặc chuyển động ngược.
• Kết luận: Như vậy, vận tốc trung bình có thể mang giá trị âm nếu độ dời của vật thể âm. Điều này phản ánh tính chất định hướng của vận tốc trong không gian ba chiều, giúp ta hiểu rõ hơn về chuyển động thực tế.

Việc tính toán vận tốc trung bình là một phần quan trọng trong việc phân tích chuyển động của một vật thể. Để tính vận tốc trung bình, chúng ta sử dụng công thức:

Trong đó:

• \(\Delta x\) là độ dời của vật thể (khoảng cách từ vị trí ban đầu đến vị trí cuối cùng).
• \(\Delta t\) là khoảng thời gian vật thể di chuyển.

Đồ thị vận tốc trung bình thường được vẽ với trục tung thể hiện vận tốc \(\overline{v}\) và trục hoành thể hiện thời gian \(\Delta t\). Dưới đây là các bước cơ bản để tính toán và vẽ đồ thị vận tốc trung bình:

1. Xác định độ dời \(\Delta x\): Đo khoảng cách từ điểm xuất phát đến điểm cuối cùng.
2. Xác định thời gian \(\Delta t\): Đo thời gian từ khi vật bắt đầu di chuyển đến khi nó dừng lại.
3. Tính vận tốc trung bình \(\overline{v}\): Áp dụng công thức \(\overline{v} = \frac{\Delta x}{\Delta t}\) để tìm vận tốc trung bình.
4. Vẽ đồ thị: Trên đồ thị, đặt thời gian \(\Delta t\) trên trục hoành (trục x) và vận tốc trung bình \(\overline{v}\) trên trục tung (trục y). Nối các điểm lại với nhau để có đồ thị vận tốc theo thời gian.

Đồ thị vận tốc trung bình giúp ta dễ dàng nhận thấy những thay đổi trong quá trình di chuyển của vật thể, từ đó phân tích sâu hơn về chuyển động của nó.

Vận tốc trung bình là một khái niệm cơ bản và quan trọng trong vật lý, giúp chúng ta phân tích và hiểu rõ hơn về chuyển động của các vật thể. Mặc dù vận tốc trung bình thường được biểu diễn bằng giá trị dương, tuy nhiên trong một số trường hợp đặc biệt, khi vật thể di chuyển theo hướng ngược lại, vận tốc trung bình có thể mang giá trị âm. Điều này phụ thuộc vào hướng của chuyển động so với hệ quy chiếu được chọn. Bằng việc hiểu rõ các yếu tố ảnh hưởng đến vận tốc trung bình và cách tính toán chính xác, chúng ta có thể áp dụng kiến thức này vào nhiều lĩnh vực khác nhau trong đời sống hàng ngày, từ giao thông đến khoa học kỹ thuật.