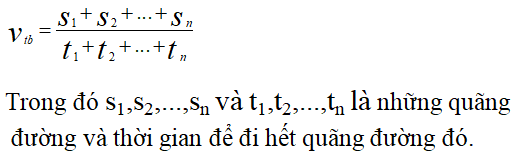Công Thức Tính Vận Tốc Thời Gian Quãng Đường: Hướng Dẫn Chi Tiết Và Ứng Dụng Thực Tế

Trong toán học và vật lý, công thức tính vận tốc, quãng đường và thời gian là những kiến thức cơ bản giúp chúng ta hiểu rõ hơn về chuyển động của các vật thể. Dưới đây là tổng hợp chi tiết các công thức và ví dụ liên quan.

Công Thức Tính Vận Tốc

Vận tốc là đại lượng vector, cho biết mức độ nhanh hay chậm của một vật thể di chuyển theo một hướng nhất định. Công thức tính vận tốc được xác định như sau:

\[
v = \frac{S}{t}
\]

Trong đó:

• \(v\) là vận tốc của vật (đơn vị: m/s, km/h,...)
• \(S\) là quãng đường vật đi được (đơn vị: m, km,...)
• \(t\) là thời gian đi hết quãng đường đó (đơn vị: s, h,...)

Công Thức Tính Quãng Đường

Khi biết vận tốc và thời gian, ta có thể tính được quãng đường mà vật đã di chuyển bằng công thức:

\[
S = v \times t
\]

Công Thức Tính Thời Gian

Ngược lại, nếu biết vận tốc và quãng đường, thời gian di chuyển có thể được tính bằng công thức:

\[
t = \frac{S}{v}
\]

Ví Dụ Minh Họa

1. Ví dụ 1: Một ô tô di chuyển từ điểm A đến điểm B với quãng đường là 150 km trong thời gian 3 giờ. Vận tốc của ô tô được tính như sau:

   \[
   v = \frac{150 \text{ km}}{3 \text{ giờ}} = 50 \text{ km/h}
   \]

2. Ví dụ 2: Một người đi bộ với vận tốc 5 km/h trong vòng 2 giờ. Quãng đường mà người đó đã đi được là:

   \[
   S = 5 \text{ km/h} \times 2 \text{ giờ} = 10 \text{ km}
   \]

3. Ví dụ 3: Một xe máy đi được quãng đường 60 km với vận tốc 30 km/h. Thời gian mà xe máy di chuyển là:

   \[
   t = \frac{60 \text{ km}}{30 \text{ km/h}} = 2 \text{ giờ}
   \]

Lưu Ý Khi Sử Dụng Công Thức

• Cần chú ý đến đơn vị đo của các đại lượng. Đảm bảo rằng các đơn vị đo lường phù hợp và đồng nhất khi áp dụng các công thức.
• Khi tính toán, nếu gặp kết quả với đơn vị không phù hợp, cần chuyển đổi đơn vị trước khi thực hiện phép tính.

Tính Toán Nâng Cao

Trong các tình huống phức tạp hơn, công thức tính vận tốc có thể được mở rộng để áp dụng cho các trường hợp chuyển động có gia tốc, chuyển động tròn, hoặc các loại chuyển động khác.

Trên đây là tổng hợp các công thức cơ bản và các lưu ý khi sử dụng chúng trong việc tính toán vận tốc, thời gian, và quãng đường. Các công thức này không chỉ giúp bạn hiểu rõ hơn về lý thuyết mà còn áp dụng hiệu quả trong thực tế cuộc sống.

Trong vật lý học và toán học, các khái niệm vận tốc, thời gian và quãng đường là những yếu tố cơ bản để hiểu về chuyển động của các vật thể. Những khái niệm này không chỉ quan trọng trong lý thuyết mà còn có nhiều ứng dụng trong đời sống hàng ngày và các ngành khoa học kỹ thuật.

• Vận Tốc: Vận tốc là đại lượng vector, cho biết mức độ nhanh hay chậm của một vật thể di chuyển theo một hướng xác định. Công thức cơ bản để tính vận tốc là \[v = \frac{S}{t}\], trong đó \(v\) là vận tốc, \(S\) là quãng đường đi được, và \(t\) là thời gian.
• Thời Gian: Thời gian là khoảng thời gian mà một sự kiện xảy ra hoặc một vật thể di chuyển từ vị trí này đến vị trí khác. Thời gian thường được đo bằng đơn vị giây, phút, giờ, và công thức để tính thời gian là \[t = \frac{S}{v}\].
• Quãng Đường: Quãng đường là độ dài của đường đi mà một vật thể di chuyển được. Quãng đường có thể được tính bằng cách nhân vận tốc với thời gian, với công thức \[S = v \times t\].

Hiểu rõ mối liên hệ giữa ba đại lượng này sẽ giúp bạn giải quyết các bài toán chuyển động một cách hiệu quả và chính xác.

Vận tốc là một đại lượng vật lý quan trọng dùng để mô tả chuyển động của một vật. Công thức tính vận tốc cơ bản nhất được xác định bằng tỷ số giữa quãng đường và thời gian:

Trong đó:

• v: Vận tốc (đơn vị: m/s hoặc km/h)
• s: Quãng đường (đơn vị: m hoặc km)
• t: Thời gian (đơn vị: s hoặc h)

Dưới đây là một số công thức tính vận tốc khác nhau trong các trường hợp cụ thể:

1. Vận Tốc Tức Thời

Vận tốc tức thời là tốc độ của một vật tại một thời điểm cụ thể trong quá trình chuyển động. Công thức tính vận tốc tức thời:

Trong đó:

• v: Vận tốc tức thời (đơn vị: m/s)
• ds: Vi phân của quãng đường
• dt: Vi phân của thời gian

2. Vận Tốc Trung Bình

Vận tốc trung bình được tính bằng tổng quãng đường đi được chia cho tổng thời gian di chuyển:

Trong đó:

• v_{\text{tb}}: Vận tốc trung bình (đơn vị: m/s)
• \(\Delta x\): Độ dời (m)
• \(\Delta t\): Thời gian (s)

3. Vận Tốc Cực Đại

Vận tốc cực đại là giá trị lớn nhất của vận tốc mà một vật có thể đạt được trong quá trình chuyển động:

Trong đó:

• v_{\text{max}}: Vận tốc cực đại
• ds: Vi phân của quãng đường
• dt: Vi phân của thời gian

Những công thức này giúp người học hiểu sâu hơn về các khía cạnh khác nhau của vận tốc trong các trường hợp cụ thể, từ đó áp dụng vào các bài toán thực tế hiệu quả hơn.

Quãng đường là một đại lượng quan trọng trong chuyển động, thể hiện độ dài của đường đi mà một vật thể di chuyển được. Công thức tính quãng đường phụ thuộc vào vận tốc và thời gian chuyển động của vật thể.

1. Công Thức Cơ Bản Tính Quãng Đường

Công thức cơ bản để tính quãng đường khi biết vận tốc và thời gian là:

Trong đó:

• S: Quãng đường (đơn vị: m hoặc km)
• v: Vận tốc (đơn vị: m/s hoặc km/h)
• t: Thời gian (đơn vị: s hoặc h)

2. Quãng Đường Trong Chuyển Động Thẳng Đều

Trong chuyển động thẳng đều, quãng đường được tính dựa trên vận tốc không đổi:

Ví dụ, nếu một xe di chuyển với vận tốc 60 km/h trong 2 giờ, quãng đường mà xe đi được là:

3. Quãng Đường Trong Chuyển Động Biến Đổi Đều

Trong chuyển động biến đổi đều, quãng đường đi được trong thời gian \( t \) khi biết vận tốc ban đầu \( v_0 \), gia tốc \( a \), và thời gian \( t \) là:

Trong đó:

• v_0: Vận tốc ban đầu (đơn vị: m/s)
• a: Gia tốc (đơn vị: m/s²)
• t: Thời gian (đơn vị: s)

4. Quãng Đường Trong Chuyển Động Tròn

Trong chuyển động tròn đều, quãng đường là chiều dài cung tròn mà vật thể di chuyển được, tính bằng:

Trong đó:

• r: Bán kính của quỹ đạo tròn (đơn vị: m)
• \(\theta\): Góc quét (đơn vị: rad)

Các công thức trên giúp bạn tính toán quãng đường trong nhiều tình huống khác nhau, từ chuyển động thẳng đến chuyển động tròn, qua đó áp dụng hiệu quả vào thực tế.

Thời gian là một đại lượng quan trọng trong việc xác định chuyển động của một vật thể. Khi biết vận tốc và quãng đường, chúng ta có thể tính được thời gian di chuyển của vật thể bằng các công thức sau:

1. Công Thức Cơ Bản Tính Thời Gian

Công thức cơ bản để tính thời gian khi biết vận tốc và quãng đường là:

Trong đó:

• t: Thời gian (đơn vị: s hoặc h)
• s: Quãng đường (đơn vị: m hoặc km)
• v: Vận tốc (đơn vị: m/s hoặc km/h)

2. Thời Gian Trong Chuyển Động Thẳng Đều

Trong chuyển động thẳng đều, thời gian di chuyển của vật thể được tính theo công thức:

Ví dụ, nếu một xe di chuyển với vận tốc 80 km/h và đi được quãng đường 160 km, thời gian xe di chuyển là:

3. Thời Gian Trong Chuyển Động Biến Đổi Đều

Trong chuyển động biến đổi đều, nếu biết vận tốc ban đầu \( v_0 \), gia tốc \( a \), và quãng đường \( s \), thời gian di chuyển có thể tính bằng công thức:

Trong đó:

• v_0: Vận tốc ban đầu (đơn vị: m/s)
• a: Gia tốc (đơn vị: m/s²)
• s: Quãng đường (đơn vị: m)

4. Thời Gian Trong Chuyển Động Tròn

Trong chuyển động tròn đều, thời gian cần để hoàn thành một vòng quay có thể tính bằng công thức:

Trong đó:

• r: Bán kính quỹ đạo (đơn vị: m)
• v: Vận tốc góc (đơn vị: m/s)

Các công thức trên giúp xác định thời gian trong nhiều tình huống chuyển động khác nhau, từ chuyển động thẳng đến chuyển động tròn, từ đó áp dụng hiệu quả vào các bài toán thực tế.

Dưới đây là một số bài tập vận dụng để giúp bạn hiểu rõ hơn về các công thức tính vận tốc, thời gian, và quãng đường. Hãy làm từng bài tập theo từng bước để củng cố kiến thức và kỹ năng giải toán của mình.

Bài Tập 1: Tính Quãng Đường

Một xe hơi di chuyển với vận tốc 60 km/h trong 3 giờ. Hãy tính quãng đường mà xe hơi đã di chuyển được.

Giải:

1. Xác định các đại lượng đã cho:
   • Vận tốc \( v = 60 \, \text{km/h} \)
   • Thời gian \( t = 3 \, \text{giờ} \)
2. Sử dụng công thức tính quãng đường: \[ S = v \times t \]
3. Tính toán: \[ S = 60 \times 3 = 180 \, \text{km} \]
4. Kết luận: Quãng đường xe hơi đã đi được là 180 km.

Bài Tập 2: Tính Thời Gian

Một người đi bộ với vận tốc 5 km/h và cần phải đi một quãng đường 20 km. Hãy tính thời gian mà người đó cần để hoàn thành quãng đường.

Giải:

1. Xác định các đại lượng đã cho:
   • Vận tốc \( v = 5 \, \text{km/h} \)
   • Quãng đường \( S = 20 \, \text{km} \)
2. Sử dụng công thức tính thời gian: \[ t = \frac{S}{v} \]
3. Tính toán: \[ t = \frac{20}{5} = 4 \, \text{giờ} \]
4. Kết luận: Người đó cần 4 giờ để đi hết quãng đường 20 km.

Bài Tập 3: Tính Vận Tốc Trung Bình

Một xe máy đi từ điểm A đến điểm B với vận tốc 40 km/h trong 2 giờ đầu, sau đó tiếp tục đi từ B đến C với vận tốc 60 km/h trong 1 giờ. Hãy tính vận tốc trung bình của xe máy trên cả quãng đường từ A đến C.

Giải:

1. Tính quãng đường đi từ A đến B: \[ S_{AB} = 40 \times 2 = 80 \, \text{km}
2. Tính quãng đường đi từ B đến C: \[ S_{BC} = 60 \times 1 = 60 \, \text{km} \]
3. Tính tổng quãng đường: \[ S_{AC} = S_{AB} + S_{BC} = 80 + 60 = 140 \, \text{km} \]
4. Tính tổng thời gian: \[ t_{AC} = 2 + 1 = 3 \, \text{giờ} \]
5. Sử dụng công thức tính vận tốc trung bình: \[ v_{\text{tb}} = \frac{S_{AC}}{t_{AC}} = \frac{140}{3} \approx 46.67 \, \text{km/h} \]
6. Kết luận: Vận tốc trung bình của xe máy trên quãng đường từ A đến C là 46.67 km/h.

Các bài tập trên đây không chỉ giúp bạn nắm vững lý thuyết mà còn rèn luyện kỹ năng giải toán một cách hiệu quả. Hãy tiếp tục thực hành để nâng cao khả năng của mình.

Khi áp dụng các công thức tính vận tốc, quãng đường, và thời gian, bạn cần lưu ý một số điểm quan trọng để đảm bảo kết quả tính toán chính xác:

1. Chuyển Đổi Đơn Vị

Trong quá trình tính toán, việc chuyển đổi đơn vị là rất quan trọng để tránh sai sót. Ví dụ:

• Khi tính vận tốc, nếu quãng đường \( S \) được tính bằng kilômét (km) và thời gian \( t \) được tính bằng giờ (h), thì vận tốc \( v \) sẽ có đơn vị là km/h.
• Nếu bạn chuyển đổi thời gian từ phút sang giờ, cần chia số phút cho 60 để có giá trị đúng. Tương tự, để chuyển đổi giây sang giờ, bạn chia số giây cho 3600.

2. Sai Số Trong Tính Toán

Sai số có thể xuất hiện do nhiều nguyên nhân như sai số trong phép đo, hoặc do việc làm tròn số. Để giảm thiểu sai số:

• Sử dụng giá trị trung bình nếu có nhiều kết quả đo.
• Giữ nguyên các giá trị thập phân trong quá trình tính toán và chỉ làm tròn kết quả cuối cùng để đảm bảo độ chính xác.
• Khi tính vận tốc trung bình, nhớ rằng nó được tính bằng tỉ số giữa tổng quãng đường đi được và tổng thời gian di chuyển. Sai sót nhỏ trong các phép đo thời gian hoặc quãng đường có thể ảnh hưởng lớn đến kết quả cuối cùng.

3. Điều Kiện Áp Dụng Công Thức

Các công thức tính vận tốc, quãng đường, và thời gian thường áp dụng cho các trường hợp chuyển động đều. Đối với các chuyển động không đều (ví dụ: chuyển động có gia tốc), cần sử dụng các công thức khác phù hợp, như công thức tính vận tốc tức thời hoặc công thức có liên quan đến gia tốc.

4. Hiểu Đúng Bản Chất Các Đại Lượng

Đảm bảo bạn hiểu rõ bản chất của các đại lượng vật lý liên quan:

• Vận tốc là một đại lượng vectơ có hướng, khác với tốc độ (là đại lượng vô hướng).
• Thời gian luôn luôn phải là khoảng thời gian thực sự mà vật chuyển động, không bao gồm thời gian nghỉ nếu có.

5. Kiểm Tra Kết Quả Tính Toán

Sau khi tính toán, hãy kiểm tra lại kết quả để đảm bảo tính logic. Ví dụ, với cùng một quãng đường, thời gian di chuyển ngắn hơn sẽ dẫn đến vận tốc lớn hơn và ngược lại.

Các công thức tính vận tốc, quãng đường và thời gian không chỉ là nền tảng quan trọng trong vật lý mà còn có ứng dụng rộng rãi trong nhiều lĩnh vực của cuộc sống và kỹ thuật. Dưới đây là một số ví dụ minh họa về cách các công thức này được áp dụng trong thực tế:

1. Ứng Dụng Trong Đời Sống Hàng Ngày

• Tính quãng đường và thời gian di chuyển: Khi đi du lịch, bạn có thể sử dụng công thức \( s = v \times t \) để tính toán quãng đường bạn sẽ đi được trong một khoảng thời gian nhất định với vận tốc trung bình. Điều này giúp bạn lên kế hoạch lộ trình hợp lý.
• Tính thời gian di chuyển: Nếu biết quãng đường và vận tốc, bạn có thể sử dụng công thức \( t = \frac{s}{v} \) để ước tính thời gian cần thiết để đến nơi. Điều này rất hữu ích khi lên kế hoạch cho các cuộc hẹn hoặc các chuyến đi.

2. Ứng Dụng Trong Các Ngành Kỹ Thuật

• Thiết kế và kiểm soát giao thông: Trong lĩnh vực giao thông, các kỹ sư sử dụng các công thức này để tính toán vận tốc và quãng đường nhằm đảm bảo an toàn và hiệu quả của các phương tiện di chuyển trên đường bộ, đường sắt và đường hàng không. Ví dụ, họ có thể tính toán khoảng cách cần thiết để một chiếc xe có thể dừng lại an toàn khi phanh dựa trên vận tốc hiện tại của nó.
• Ứng dụng trong cơ khí: Trong việc thiết kế máy móc, kỹ sư cần tính toán vận tốc của các bộ phận chuyển động để đảm bảo chúng hoạt động trơn tru và an toàn. Ví dụ, việc tính toán vận tốc góc \( \omega = \frac{\Delta \theta}{\Delta t} \) rất quan trọng trong thiết kế các hệ thống quay như bánh răng, trục khuỷu.
• Quản lý năng lượng: Trong ngành năng lượng, việc tính toán chính xác quãng đường và thời gian di chuyển của các dòng khí hoặc chất lỏng trong ống dẫn giúp tối ưu hóa việc tiêu thụ năng lượng, giảm thiểu tổn thất.

Như vậy, các công thức tính vận tốc, quãng đường và thời gian không chỉ là lý thuyết mà còn có những ứng dụng thực tế quan trọng, từ việc lập kế hoạch cá nhân hàng ngày đến thiết kế và quản lý các hệ thống kỹ thuật phức tạp.