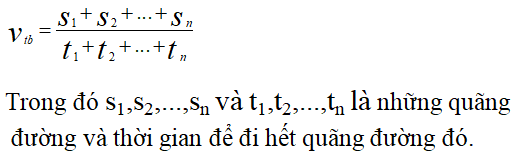Chủ đề khi vận tốc của vật tăng gấp đôi thì: Khi vận tốc của vật tăng gấp đôi, nhiều yếu tố quan trọng trong vật lý sẽ thay đổi đáng kể. Bài viết này sẽ khám phá chi tiết những tác động và ứng dụng của việc tăng vận tốc, từ động năng, động lượng đến các ứng dụng thực tế, giúp bạn hiểu rõ hơn về hiện tượng này trong đời sống và khoa học.
Mục lục
Khi Vận Tốc Của Vật Tăng Gấp Đôi Thì
Khi vận tốc của một vật tăng gấp đôi, nhiều đại lượng vật lý khác cũng thay đổi theo. Dưới đây là các hệ quả chính:
1. Động năng tăng gấp bốn
Động năng \(K\) của một vật được tính bằng công thức:
\[K = \frac{1}{2}mv^2\]
Với \(m\) là khối lượng của vật và \(v\) là vận tốc. Khi vận tốc tăng gấp đôi, tức là \(v' = 2v\), động năng sẽ là:
\[K' = \frac{1}{2}m(2v)^2 = 4\left(\frac{1}{2}mv^2\right) = 4K\]
Vậy động năng của vật sẽ tăng gấp bốn lần.
2. Động lượng tăng gấp đôi
Động lượng \(p\) của một vật được tính bằng công thức:
\[p = mv\]
Nếu vận tốc tăng gấp đôi, tức là \(v' = 2v\), động lượng mới sẽ là:
\[p' = m(2v) = 2mv = 2p\]
Vậy động lượng sẽ tăng gấp đôi.
3. Gia tốc và thế năng không thay đổi
Gia tốc và thế năng không phụ thuộc vào vận tốc mà phụ thuộc vào các yếu tố khác như lực tác dụng và vị trí trong trường lực, do đó khi vận tốc tăng gấp đôi, các đại lượng này không thay đổi.
4. Ứng dụng và ý nghĩa
Hiểu biết về mối quan hệ giữa vận tốc và các đại lượng vật lý khác rất quan trọng trong nhiều lĩnh vực như kỹ thuật, hàng không, và vật lý ứng dụng. Điều này giúp chúng ta dự đoán và tính toán chính xác các hiện tượng xảy ra khi thay đổi vận tốc của vật.
Nhìn chung, việc tăng gấp đôi vận tốc của một vật dẫn đến sự thay đổi lớn trong các đại lượng động lực học như động năng và động lượng, điều này cần được lưu ý trong các tính toán và thiết kế liên quan đến chuyển động.

.png)
1. Động Năng Của Vật
Động năng là một dạng năng lượng mà một vật sở hữu do chuyển động của nó. Động năng của một vật có khối lượng \(m\) và vận tốc \(v\) được xác định bằng công thức:
\[K = \frac{1}{2}mv^2\]
Trong đó:
- \(K\): Động năng (Joule)
- \(m\): Khối lượng của vật (kg)
- \(v\): Vận tốc của vật (m/s)
Nếu vận tốc của vật tăng gấp đôi, tức là \(v' = 2v\), động năng mới của vật sẽ là:
\[K' = \frac{1}{2}m(2v)^2 = \frac{1}{2}m(4v^2) = 4\left(\frac{1}{2}mv^2\right) = 4K\]
Điều này có nghĩa là khi vận tốc của vật tăng gấp đôi, động năng của vật sẽ tăng gấp bốn lần. Đây là một kết quả quan trọng trong vật lý, vì nó cho thấy rằng động năng phụ thuộc rất mạnh vào vận tốc của vật. Điều này cũng giải thích tại sao trong các tình huống như va chạm hoặc chuyển động nhanh, năng lượng tác động có thể rất lớn.
Hiểu rõ về sự biến đổi động năng khi vận tốc thay đổi là rất quan trọng trong nhiều ứng dụng thực tế, từ thiết kế xe cộ, máy móc đến các nghiên cứu về an toàn và tiết kiệm năng lượng.
2. Động Lượng Của Vật
Động lượng là một đại lượng vật lý đặc trưng cho chuyển động của một vật, được xác định bởi tích của khối lượng và vận tốc của vật đó. Công thức tính động lượng \(p\) của một vật có khối lượng \(m\) và vận tốc \(v\) là:
\[p = mv\]
Trong đó:
- \(p\): Động lượng (kg·m/s)
- \(m\): Khối lượng của vật (kg)
- \(v\): Vận tốc của vật (m/s)
Nếu vận tốc của vật tăng gấp đôi, tức là \(v' = 2v\), động lượng mới của vật sẽ là:
\[p' = m \cdot 2v = 2mv = 2p\]
Điều này cho thấy khi vận tốc của vật tăng gấp đôi, động lượng của vật cũng tăng gấp đôi. Đây là một kết quả trực tiếp từ công thức động lượng và là một yếu tố quan trọng trong các hiện tượng va chạm và bảo toàn động lượng trong cơ học. Trong nhiều trường hợp, động lượng là đại lượng bảo toàn, nghĩa là tổng động lượng trước và sau va chạm vẫn giữ nguyên, làm cho nó trở thành một công cụ quan trọng trong việc phân tích các tình huống vật lý phức tạp.
Việc hiểu rõ mối quan hệ giữa vận tốc và động lượng giúp chúng ta có cái nhìn sâu sắc hơn về cách các vật thể tương tác trong chuyển động, đồng thời cung cấp cơ sở lý thuyết cho các ứng dụng thực tế như thiết kế phương tiện giao thông, các hệ thống va chạm và nhiều lĩnh vực khoa học kỹ thuật khác.

3. Ảnh Hưởng Đến Các Đại Lượng Khác
3.1. Gia tốc và sự thay đổi
Gia tốc của vật không thay đổi trực tiếp khi vận tốc tăng gấp đôi, vì gia tốc phụ thuộc vào lực tác dụng lên vật và khối lượng của vật, theo định luật II của Newton:
\[ F = ma \]
Tuy nhiên, trong các hệ thống có ma sát, lực cản không khí, hay các lực khác liên quan đến vận tốc, gia tốc có thể thay đổi gián tiếp do những lực này tăng lên khi vận tốc tăng.
3.2. Thế năng và mối quan hệ với vận tốc
Thế năng, đặc biệt là thế năng hấp dẫn, không phụ thuộc vào vận tốc của vật, mà phụ thuộc vào vị trí của nó trong trường thế năng:
\[ W = mgh \]
Tuy nhiên, khi vận tốc tăng, tổng năng lượng của hệ thống (gồm cả động năng và thế năng) có thể thay đổi nếu vận tốc đủ lớn để vật thay đổi độ cao hay vị trí trong trường thế năng.
3.3. Các đại lượng không phụ thuộc vận tốc
Các đại lượng như khối lượng (\[ m \]), thời gian (\[ t \]), và nhiệt độ (\[ T \]) của vật không bị ảnh hưởng bởi sự thay đổi của vận tốc. Những đại lượng này độc lập với sự biến đổi của vận tốc và không chịu ảnh hưởng trực tiếp khi vận tốc tăng hay giảm.
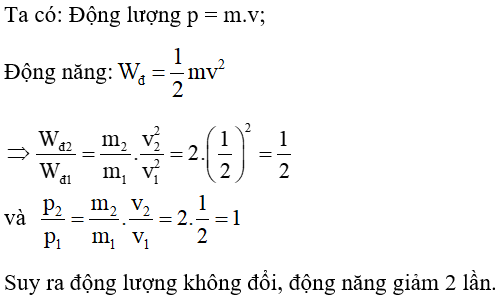
4. Tổng Kết Và Ứng Dụng
Khi vận tốc của một vật tăng gấp đôi, các đại lượng liên quan đến chuyển động của vật cũng có sự thay đổi đáng kể. Điều này không chỉ quan trọng trong các phép tính toán học mà còn có ý nghĩa thực tiễn lớn trong nhiều lĩnh vực khoa học và kỹ thuật.
4.1. Ý nghĩa của việc thay đổi vận tốc
Việc tăng gấp đôi vận tốc của vật dẫn đến một loạt các thay đổi trong các đại lượng vật lý:
- Động năng: Động năng của vật tỷ lệ thuận với bình phương của vận tốc, do đó khi vận tốc tăng gấp đôi, động năng tăng lên gấp bốn lần. Điều này cho thấy một sự gia tăng mạnh mẽ trong năng lượng cần thiết để đạt được hoặc duy trì tốc độ cao hơn.
- Động lượng: Động lượng của vật là tích của khối lượng và vận tốc. Khi vận tốc tăng gấp đôi, động lượng cũng tăng gấp đôi. Điều này đặc biệt quan trọng trong các va chạm và tương tác động học, nơi động lượng được bảo toàn.
- Thế năng: Trong nhiều trường hợp, đặc biệt là khi xét đến năng lượng cơ học tổng hợp, việc tăng vận tốc có thể ảnh hưởng đến thế năng, nhất là trong các hệ thống có chuyển động phức tạp hoặc khi có sự tương tác với các trường lực khác.
4.2. Ứng dụng trong các lĩnh vực khoa học
Những thay đổi trên không chỉ là lý thuyết mà còn có ứng dụng thực tiễn trong nhiều lĩnh vực:
- Trong ngành hàng không và vũ trụ: Hiểu rõ mối quan hệ giữa vận tốc và các đại lượng như động năng, động lượng giúp tối ưu hóa việc thiết kế máy bay, tàu vũ trụ, và tên lửa, từ đó nâng cao hiệu quả nhiên liệu và đảm bảo an toàn cho hành trình.
- Trong ngành ô tô: Khả năng kiểm soát vận tốc một cách chính xác là yếu tố then chốt để đảm bảo an toàn giao thông, đồng thời giảm thiểu tác động của các vụ tai nạn. Việc tăng tốc hay giảm tốc đều đòi hỏi sự cân nhắc kỹ lưỡng về động năng và động lượng.
- Trong lĩnh vực thể thao: Các vận động viên, đặc biệt trong các môn đua xe, điền kinh, phải hiểu rõ ảnh hưởng của vận tốc để tối ưu hóa hiệu suất và tránh chấn thương.
4.3. Kết luận
Việc tăng gấp đôi vận tốc của vật không chỉ đơn thuần là một thay đổi trong thông số chuyển động, mà còn ảnh hưởng đến nhiều khía cạnh khác nhau của vật lý và ứng dụng thực tế. Hiểu rõ các tác động này giúp chúng ta có thể áp dụng vào thực tế một cách hiệu quả, từ việc thiết kế các phương tiện giao thông đến tối ưu hóa trong các môn thể thao và nhiều lĩnh vực khác.