Chủ đề một proton chuyển động thẳng đều: Một proton chuyển động thẳng đều là hiện tượng vật lý thú vị, đặc biệt khi proton di chuyển trong môi trường từ trường và điện trường đều. Bài viết này sẽ giúp bạn hiểu rõ cơ chế, các yếu tố ảnh hưởng và ứng dụng của chuyển động này trong các ngành khoa học và công nghệ hiện đại. Tìm hiểu sâu hơn về cách thức và vai trò của proton trong các hệ thống kỹ thuật phức tạp!
Mục lục
Một Proton Chuyển Động Thẳng Đều
Một proton chuyển động thẳng đều trong một môi trường có thể bao gồm từ trường đều và điện trường đều. Để hiểu rõ hơn về quá trình này, chúng ta cần nắm bắt các khái niệm cơ bản về lực tác động, phương trình chuyển động, và các yếu tố liên quan.
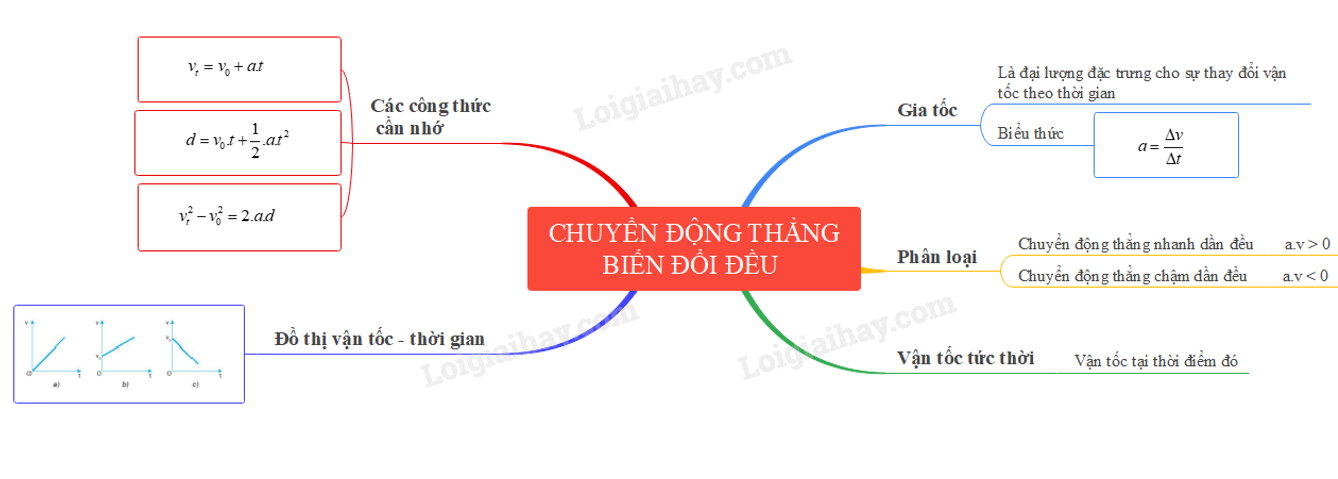
1. Định Nghĩa Chuyển Động Thẳng Đều
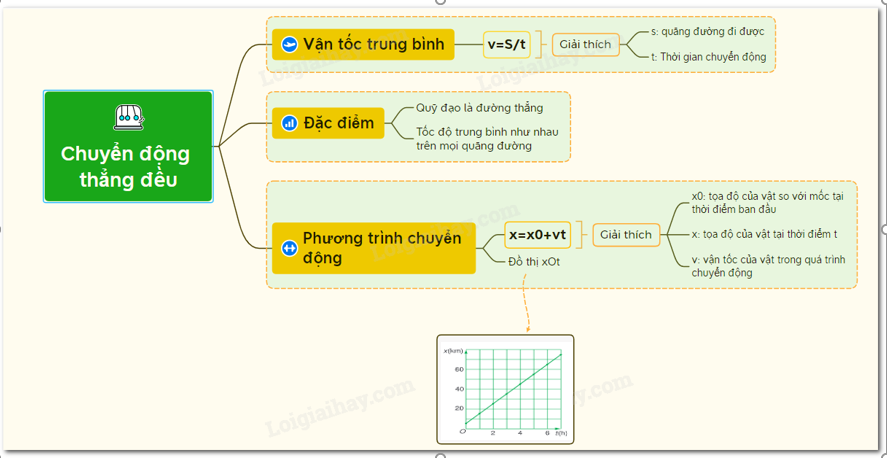
Chuyển động thẳng đều là một loại chuyển động trong đó vận tốc của vật không thay đổi theo thời gian, tức là vật di chuyển theo một đường thẳng với vận tốc không đổi. Phương trình mô tả chuyển động thẳng đều là:
Trong đó:
- \(x\) là vị trí của vật tại thời điểm \(t\).
- \(x_{0}\) là vị trí ban đầu của vật.
- \(v\) là vận tốc của vật.
- \(t\) là thời gian.
2. Ứng Dụng Trong Bài Toán Vật Lý
Một ví dụ về proton chuyển động thẳng đều là khi nó di chuyển trong một miền có từ trường đều và điện trường đều. Trong trường hợp này, các lực điện và từ có thể tác động lên proton theo các hướng khác nhau, nhưng tổng hợp lại tạo ra một chuyển động thẳng đều. Phương trình lực Lorentz có thể được áp dụng để phân tích lực tác động lên proton:
Trong đó:
- \(\vec{F}\) là lực tác động lên proton.
- \(q\) là điện tích của proton.
- \(\vec{E}\) là cường độ điện trường.
- \(\vec{v}\) là vận tốc của proton.
- \(\vec{B}\) là cảm ứng từ.
3. Phân Tích Đồ Thị Chuyển Động Thẳng Đều
Đồ thị biểu diễn chuyển động thẳng đều có dạng là một đường thẳng trong mặt phẳng tọa độ \(x-t\), với độ dốc của đường thẳng thể hiện vận tốc của vật:
Nếu đồ thị có độ dốc dương, điều đó biểu thị vật đang di chuyển theo chiều dương của trục \(x\). Ngược lại, nếu độ dốc âm, vật đang di chuyển theo chiều ngược lại.
4. Kết Luận
Chuyển động thẳng đều của proton là một ví dụ cơ bản nhưng quan trọng trong việc hiểu các nguyên lý cơ bản của vật lý. Nó không chỉ áp dụng trong các bài toán lý thuyết mà còn có thể áp dụng trong các bài toán thực tế, nơi các hạt tích điện di chuyển trong môi trường có từ trường và điện trường.
.png)
1. Khái niệm về chuyển động thẳng đều
Chuyển động thẳng đều là chuyển động có quỹ đạo thẳng, trong đó vật di chuyển với vận tốc không đổi theo thời gian. Điều này có nghĩa là vận tốc của vật không thay đổi về cả độ lớn lẫn hướng, và gia tốc bằng không. Công thức tính vận tốc trong chuyển động thẳng đều là:
Trong đó:
- \(v\) là vận tốc (m/s)
- \(s\) là quãng đường đi được (m)
- \(t\) là thời gian (s)
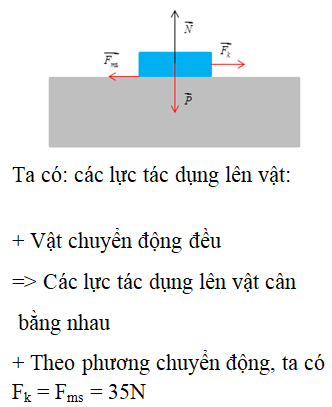
Đặc điểm quan trọng của chuyển động thẳng đều là lực tác động lên vật phải cân bằng, hoặc không có lực tác động. Điều này giúp vật duy trì vận tốc không đổi theo thời gian.
2. Proton trong từ trường và điện trường
Một proton mang điện tích dương, chuyển động trong cả từ trường đều và điện trường đều sẽ chịu tác dụng của hai lực chính: lực điện và lực từ.
- Lực điện: Lực này tác dụng lên proton khi nó nằm trong điện trường có cường độ \( \mathbf{E} \). Theo định luật Coulomb, lực điện tác dụng lên proton được tính bằng công thức: \[ \mathbf{F}_e = q \mathbf{E} \] với \( q \) là điện tích của proton.
- Lực từ: Khi proton chuyển động với vận tốc \( \mathbf{v} \) trong từ trường có cảm ứng từ \( \mathbf{B} \), lực Lorentz tác dụng lên nó là: \[ \mathbf{F}_m = q (\mathbf{v} \times \mathbf{B}) \] Lực này luôn vuông góc với cả vận tốc và từ trường, làm proton chuyển động theo quỹ đạo xoắn ốc hoặc tròn.
Nếu vectơ vận tốc \( \mathbf{v} \), vectơ điện trường \( \mathbf{E} \) và từ trường \( \mathbf{B} \) có các hướng vuông góc với nhau, proton có thể chuyển động thẳng đều nếu lực điện và lực từ cân bằng nhau. Điều kiện này được mô tả bởi phương trình:
Hay rút gọn ta có:
Trong trường hợp này, vận tốc của proton được tính như sau:
Điều này cho thấy proton sẽ chuyển động thẳng đều với vận tốc không đổi khi cường độ điện trường và từ trường được thiết lập hợp lý.
| Tham số | Ký hiệu | Đơn vị |
| Điện tích của proton | \( q \) | Coulomb (C) |
| Vận tốc | \( v \) | m/s |
| Cường độ điện trường | \( E \) | V/m |
| Cảm ứng từ | \( B \) | Tesla (T) |
Do vậy, proton có thể duy trì chuyển động thẳng đều khi hai lực này cân bằng nhau, hoặc nếu chỉ một lực tác dụng trong trường hợp điện trường hoặc từ trường bị loại bỏ.

3. Hệ tọa độ Oxyz và lực tác dụng
Trong bài toán vật lý, hệ tọa độ Oxyz thường được sử dụng để mô tả chuyển động của proton trong không gian ba chiều. Hệ tọa độ này gồm ba trục chính: trục \( Ox \), trục \( Oy \) và trục \( Oz \), với mỗi trục đại diện cho một chiều trong không gian. Vị trí của proton tại một thời điểm bất kỳ có thể được biểu diễn dưới dạng tọa độ \( (x, y, z) \).
Khi proton chuyển động thẳng đều trong hệ tọa độ Oxyz, các lực tác dụng lên nó sẽ được phân tích thành các thành phần theo ba trục:
- Thành phần theo trục \( Ox \): Lực tác dụng theo phương ngang, ký hiệu là \( F_x \).
- Thành phần theo trục \( Oy \): Lực tác dụng theo phương thẳng đứng, ký hiệu là \( F_y \).
- Thành phần theo trục \( Oz \): Lực tác dụng theo phương sâu vào hoặc ra ngoài không gian, ký hiệu là \( F_z \).
Tổng hợp các lực này, lực tổng hợp \( \mathbf{F} \) sẽ được tính bằng cách sử dụng định lý Pythagore trong không gian ba chiều:
Chuyển động của proton trong hệ tọa độ Oxyz có thể được phân tích theo các trục để hiểu rõ tác động của các lực trong từng chiều không gian. Khi các lực cân bằng nhau, proton sẽ duy trì trạng thái chuyển động thẳng đều với vận tốc không đổi.
| Thành phần lực | Ký hiệu | Đơn vị |
| Lực theo trục Ox | \( F_x \) | Newton (N) |
| Lực theo trục Oy | \( F_y \) | Newton (N) |
| Lực theo trục Oz | \( F_z \) | Newton (N) |
Phân tích lực trong hệ tọa độ Oxyz giúp chúng ta dễ dàng dự đoán và xác định được quỹ đạo của proton trong không gian ba chiều, cũng như cách các lực tương tác với proton khi nó chuyển động.

4. Các ví dụ và bài tập thực hành
Để hiểu rõ hơn về chuyển động thẳng đều của proton, dưới đây là một số ví dụ và bài tập thực hành giúp bạn củng cố kiến thức. Các bài tập được phân tích chi tiết, từ đó giúp người học dễ dàng tiếp cận và giải quyết các vấn đề liên quan.
Ví dụ 1: Proton chuyển động trong điện trường đều
Một proton có vận tốc ban đầu \( v_0 = 2 \times 10^6 \, \text{m/s} \) di chuyển thẳng đều trong điện trường đều với cường độ \( E = 10^3 \, \text{N/C} \). Hãy tính gia tốc của proton và xác định quãng đường nó di chuyển trong thời gian \( t = 5 \, \text{s} \).
- Giải: Tính lực tác dụng lên proton: \( F = q \cdot E \)
- Tính gia tốc của proton: \( a = \frac{F}{m} \)
- Tính quãng đường di chuyển: \( s = v_0 \cdot t + \frac{1}{2} a \cdot t^2 \)
Ví dụ 2: Proton di chuyển dưới tác dụng của từ trường
Một proton với vận tốc ban đầu \( v_0 = 1.5 \times 10^6 \, \text{m/s} \) di chuyển thẳng đều trong từ trường đều có độ lớn \( B = 0.5 \, \text{T} \). Xác định lực Lorentz tác dụng lên proton và mô tả quỹ đạo của nó.
- Giải: Lực Lorentz được tính bằng công thức: \( F = q \cdot v_0 \cdot B \)
- Xác định quỹ đạo của proton: proton sẽ chuyển động theo quỹ đạo xoắn ốc hoặc tròn phụ thuộc vào góc giữa \( \vec{v} \) và \( \vec{B} \).
Bài tập tự luyện
- Một proton chuyển động thẳng đều với vận tốc \( v = 3 \times 10^6 \, \text{m/s} \). Hãy tính khoảng cách proton di chuyển trong \( t = 10 \, \text{s} \).
- Một proton chịu tác dụng của lực điện trường và từ trường. Viết phương trình mô tả quỹ đạo của proton.
- Tính năng lượng của proton khi di chuyển trong điện trường có cường độ \( E = 500 \, \text{N/C} \).

5. Tổng hợp kiến thức
Qua những phần trước, chúng ta đã tìm hiểu về các khái niệm cơ bản liên quan đến chuyển động thẳng đều của proton trong các môi trường như điện trường và từ trường, cùng với các ví dụ và bài tập thực hành. Phần này sẽ tổng hợp lại những kiến thức quan trọng, giúp bạn có cái nhìn toàn diện hơn về chủ đề này.
- Chuyển động thẳng đều là gì? Đây là chuyển động với vận tốc không đổi theo thời gian, tức là không có gia tốc.
- Trong điện trường, proton chịu tác động của lực điện \( F = q \cdot E \), dẫn đến gia tốc và thay đổi quỹ đạo.
- Trong từ trường, proton chịu tác động của lực Lorentz \( F = q \cdot v \cdot B \), làm cho quỹ đạo của nó có thể là đường cong hoặc xoắn ốc.
- Hệ tọa độ Oxyz giúp mô tả chính xác vị trí và quỹ đạo của proton trong không gian ba chiều.
- Qua các ví dụ và bài tập thực hành, người học có thể áp dụng kiến thức để tính toán các đại lượng liên quan đến chuyển động của proton.
Từ những kiến thức này, bạn sẽ có nền tảng vững chắc để nghiên cứu sâu hơn về chuyển động của các hạt điện tích trong các môi trường vật lý khác nhau.