Một ô tô chuyển động thẳng nhanh dần đều sau 10s: Phân tích và Ứng dụng

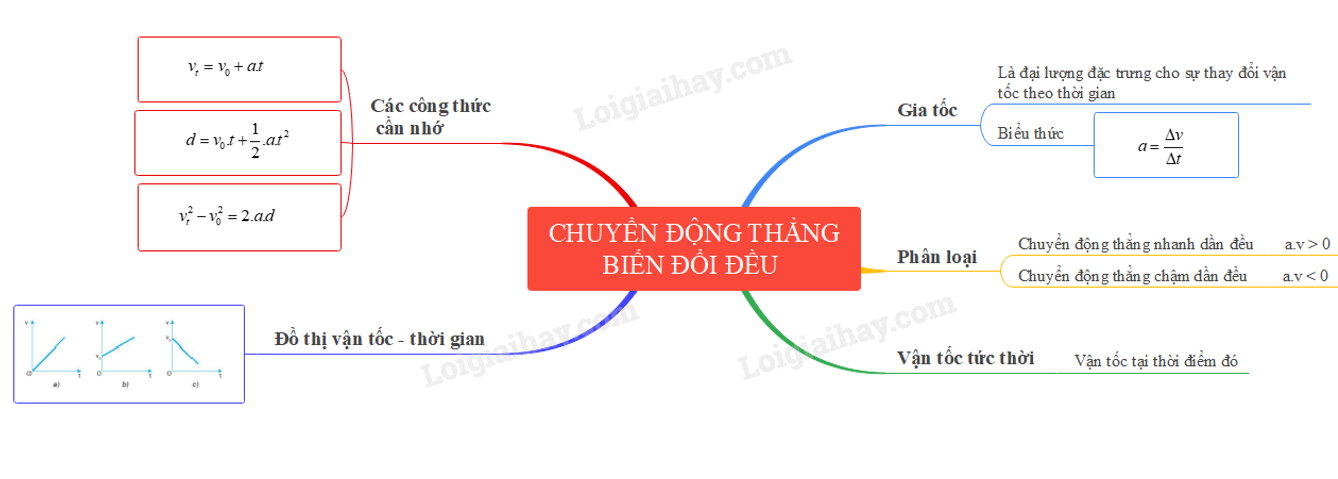
Chuyển động thẳng nhanh dần đều là một dạng chuyển động cơ học trong đó vận tốc của vật thay đổi đều theo thời gian. Bài toán về ô tô chuyển động nhanh dần đều sau 10 giây được giải dựa trên các công thức cơ bản của chuyển động thẳng biến đổi đều trong vật lý.

Công thức tính vận tốc trong chuyển động thẳng nhanh dần đều

Vận tốc \(v\) của ô tô sau một khoảng thời gian \(t\) được tính theo công thức:

\[
v = v_0 + at
\]
trong đó:

• \(v\) là vận tốc tại thời điểm \(t\)
• \(v_0\) là vận tốc ban đầu của ô tô
• \(a\) là gia tốc
• \(t\) là thời gian chuyển động

Quãng đường đi được sau 10 giây

Quãng đường \(s\) mà ô tô đi được sau thời gian \(t\) là:

\[
s = v_0 t + \frac{1}{2} a t^2
\]
trong đó:

• \(s\) là quãng đường đi được

Ví dụ cụ thể

Giả sử ô tô có vận tốc ban đầu là \(4 \, \text{m/s}\) và sau 10 giây, vận tốc của ô tô đạt \(6 \, \text{m/s}\). Gia tốc của ô tô được tính như sau:

\[
a = \frac{v - v_0}{t} = \frac{6 - 4}{10} = 0.2 \, \text{m/s}^2
\]

Quãng đường đi được trong 10 giây là:

\[
s = 4 \times 10 + \frac{1}{2} \times 0.2 \times 10^2 = 40 + 10 = 50 \, \text{m}
\]

Ứng dụng thực tế

Bài toán này mô tả quá trình tăng tốc đều của ô tô trong thực tế, khi người lái xe tăng ga và giữ cho gia tốc không đổi. Việc hiểu rõ cách tính vận tốc và quãng đường giúp các kỹ sư thiết kế hệ thống lái xe an toàn, hiệu quả và các tài xế tối ưu hóa hiệu suất lái xe.

Chuyển động thẳng nhanh dần đều là một loại chuyển động cơ học phổ biến, trong đó vận tốc của vật tăng đều theo thời gian. Đây là dạng chuyển động mà gia tốc không đổi, tạo ra sự thay đổi đồng đều về vận tốc của vật thể.

Công thức tổng quát để tính vận tốc trong chuyển động thẳng nhanh dần đều là:

\[
v = v_0 + at
\]
trong đó:

• \(v\) là vận tốc tại thời điểm \(t\)
• \(v_0\) là vận tốc ban đầu của vật
• \(a\) là gia tốc không đổi
• \(t\) là thời gian chuyển động

Trong trường hợp một ô tô chuyển động thẳng nhanh dần đều sau 10 giây, người ta thường quan tâm đến gia tốc và quãng đường mà ô tô đã đi được sau khoảng thời gian này. Quãng đường \(s\) được tính bằng công thức:

\[
s = v_0 t + \frac{1}{2} a t^2
\]

Đặc biệt, khi gia tốc \(a\) không đổi, bài toán trở nên đơn giản hơn và dễ dàng áp dụng trong các bài toán thực tế. Hiện tượng này xuất hiện thường xuyên trong cuộc sống hằng ngày, đặc biệt là trong các hệ thống giao thông, nơi các phương tiện thường gia tốc để đạt đến vận tốc tối ưu.

Trong chuyển động thẳng nhanh dần đều, việc tính toán vận tốc và quãng đường của một vật thể là rất quan trọng. Vận tốc của vật thể thay đổi đều theo thời gian, và quãng đường di chuyển cũng phụ thuộc vào sự thay đổi này.

Công thức tính vận tốc:

Vận tốc tức thời của vật thể trong chuyển động thẳng nhanh dần đều được tính bằng công thức:

\[
v = v_0 + at
\]
trong đó:

• \(v\) là vận tốc tại thời điểm \(t\)
• \(v_0\) là vận tốc ban đầu
• \(a\) là gia tốc không đổi
• \(t\) là thời gian chuyển động

Công thức tính quãng đường:

Quãng đường mà vật thể di chuyển được trong khoảng thời gian \(t\) được tính theo công thức sau:

\[
s = v_0 t + \frac{1}{2} a t^2
\]
trong đó:

• \(s\) là quãng đường di chuyển được
• \(v_0\) là vận tốc ban đầu
• \(t\) là thời gian di chuyển
• \(a\) là gia tốc không đổi

Ví dụ, nếu một ô tô chuyển động thẳng nhanh dần đều trong 10 giây với vận tốc ban đầu \(v_0 = 0\) và gia tốc \(a = 2 \, m/s^2\), ta có thể tính quãng đường như sau:

\[
s = 0 \times 10 + \frac{1}{2} \times 2 \times 10^2 = 100 \, m
\]

Với công thức này, ta có thể áp dụng vào nhiều trường hợp khác nhau trong các bài toán thực tế và tính toán vận tốc, quãng đường một cách dễ dàng.

Trong chuyển động thẳng nhanh dần đều, gia tốc \(a\) được định nghĩa là đại lượng đặc trưng cho sự thay đổi vận tốc theo thời gian. Gia tốc là một hằng số trong suốt quá trình chuyển động.

Gia tốc \(a\) có thể được tính theo công thức:

Trong đó:

• \(\Delta v\): Độ thay đổi vận tốc (vận tốc cuối trừ vận tốc đầu).
• \(\Delta t\): Thời gian mà vận tốc thay đổi.

Ví dụ, một ô tô chuyển động thẳng nhanh dần đều với vận tốc ban đầu \(v_0 = 0 \, \text{m/s}\), sau \(10 \, \text{s}\) đạt vận tốc \(v = 20 \, \text{m/s}\). Khi đó, gia tốc \(a\) của ô tô được tính như sau:

Như vậy, gia tốc của ô tô là \(2 \, \text{m/s}^2\), tức là mỗi giây vận tốc của ô tô tăng thêm \(2 \, \text{m/s}\).

Trong thực tế, gia tốc giúp xác định sự thay đổi tốc độ của một vật khi nó di chuyển, và nó là yếu tố quan trọng để tính toán quãng đường và vận tốc trong quá trình chuyển động nhanh dần đều.

Chuyển động thẳng nhanh dần đều là dạng chuyển động mà trong đó vận tốc của vật tăng dần theo thời gian với một gia tốc không đổi. Có nhiều yếu tố ảnh hưởng đến chuyển động này, bao gồm:

• Gia tốc: Đây là yếu tố quyết định tốc độ tăng dần của vận tốc. Gia tốc càng lớn, vật càng nhanh đạt được tốc độ cao. Công thức tính vận tốc của chuyển động thẳng nhanh dần đều là: \[ v = v_0 + at \] Trong đó:
  • \(v\) là vận tốc của vật tại thời điểm \(t\).
  • \(v_0\) là vận tốc ban đầu của vật.
  • \(a\) là gia tốc (m/s²).
  • \(t\) là thời gian chuyển động (s).
• Thời gian: Thời gian chuyển động ảnh hưởng trực tiếp đến vận tốc và quãng đường mà vật đi được. Quãng đường \(s\) đi được trong chuyển động thẳng nhanh dần đều được tính theo công thức: \[ s = v_0 t + \frac{1}{2}at^2 \]
• Vận tốc ban đầu: Nếu vật bắt đầu chuyển động với vận tốc ban đầu \(v_0\), vận tốc này sẽ là cơ sở để gia tốc tiếp tục làm tăng vận tốc sau đó. Khi vận tốc ban đầu bằng 0, phương trình chuyển động có thể được đơn giản hóa.
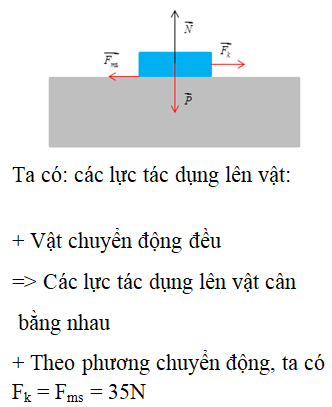
• Lực tác động: Lực tác động vào vật (như lực kéo của động cơ ô tô) là nguyên nhân chính tạo ra gia tốc. Gia tốc lớn hay nhỏ phụ thuộc vào độ lớn của lực tác động theo định luật II Newton: \[ F = ma \] Trong đó:
  • \(F\) là lực tác động (N).
  • \(m\) là khối lượng của vật (kg).
  • \(a\) là gia tốc (m/s²).
• Ma sát: Ma sát giữa bề mặt chuyển động và vật sẽ làm giảm tốc độ tăng của vận tốc, nghĩa là ảnh hưởng trực tiếp đến gia tốc. Gia tốc thực tế sẽ là kết quả của sự cân bằng giữa lực kéo và lực cản do ma sát.

Tóm lại, chuyển động thẳng nhanh dần đều chịu ảnh hưởng của nhiều yếu tố như gia tốc, thời gian, vận tốc ban đầu, lực tác động và ma sát. Sự phối hợp giữa các yếu tố này quyết định tốc độ và quãng đường di chuyển của vật trong chuyển động.

Để giúp bạn hiểu rõ hơn về chuyển động thẳng nhanh dần đều, dưới đây là một số bài tập ví dụ và ứng dụng thực tiễn:

5.1. Bài tập ví dụ

Bài 1: Một ô tô đang di chuyển với vận tốc ban đầu \( v_0 = 12 \, \text{m/s} \). Sau khi tăng ga, xe bắt đầu chuyển động thẳng nhanh dần đều với gia tốc \( a = 0.2 \, \text{m/s}^2 \). Hãy tính vận tốc và quãng đường mà ô tô đi được sau 30 giây.

• Vận tốc sau 30 giây: \[ v = v_0 + at = 12 + 0.2 \times 30 = 18 \, \text{m/s} \]
• Quãng đường ô tô đi được: \[ s = v_0 t + \frac{1}{2} a t^2 = 12 \times 30 + \frac{1}{2} \times 0.2 \times 30^2 = 450 \, \text{m} \]

5.2. Ứng dụng thực tiễn

Chuyển động thẳng nhanh dần đều có ứng dụng rộng rãi trong thực tế, từ các phương tiện giao thông đến các máy móc công nghiệp. Ví dụ, khi một chiếc ô tô tăng tốc trên đường cao tốc hoặc khi một đoàn tàu rời ga, cả hai đều là những trường hợp chuyển động thẳng nhanh dần đều. Cụ thể:

• Ô tô tăng tốc: Khi một ô tô di chuyển với vận tốc ban đầu và tài xế nhấn ga, xe sẽ tăng tốc với một gia tốc không đổi. Ví dụ, khi xe đạt vận tốc \( 15 \, \text{m/s} \) sau 10 giây, bạn có thể tính được quãng đường và gia tốc trong thời gian này.
• Máy móc công nghiệp: Trong các quy trình sản xuất, việc sử dụng chuyển động thẳng nhanh dần đều giúp các bộ phận máy móc tăng tốc dần để đạt hiệu suất cao nhất.

5.3. Bài tập nâng cao

Bài 2: Một ô tô chạy với vận tốc \( v_0 = 15 \, \text{m/s} \) thì tắt máy và chuyển động chậm dần đều. Sau khi đi thêm được \( 125 \, \text{m} \), vận tốc của ô tô là \( 10 \, \text{m/s} \). Hãy tính gia tốc và thời gian ô tô chuyển động trước khi dừng hẳn.

• Gia tốc của ô tô: \[ a = \frac{v^2 - v_0^2}{2s} = \frac{10^2 - 15^2}{2 \times 125} = -0.5 \, \text{m/s}^2 \]
• Thời gian chuyển động: \[ t = \frac{v - v_0}{a} = \frac{10 - 15}{-0.5} = 10 \, \text{giây} \]

Dưới đây là những câu hỏi thường gặp liên quan đến chuyển động thẳng nhanh dần đều và các giải đáp chi tiết:

• 1. Gia tốc là gì và nó có vai trò gì trong chuyển động thẳng nhanh dần đều?

Gia tốc \((a)\) là đại lượng đo tốc độ thay đổi của vận tốc theo thời gian. Trong chuyển động thẳng nhanh dần đều, gia tốc luôn không đổi và đóng vai trò quan trọng quyết định tốc độ tăng của vận tốc theo thời gian. Công thức tính vận tốc tại thời điểm bất kỳ là:

\[ v = v_0 + a \cdot t \]

Trong đó:

• \(v\): Vận tốc tại thời điểm \(t\) (m/s)
• \(v_0\): Vận tốc ban đầu (m/s)
• \(a\): Gia tốc (m/s²)
• \(t\): Thời gian chuyển động (s)
• 2. Làm thế nào để tính quãng đường trong chuyển động thẳng nhanh dần đều?

Quãng đường đi được trong chuyển động thẳng nhanh dần đều được tính bằng công thức:

\[ s = v_0 \cdot t + \frac{1}{2} \cdot a \cdot t^2 \]

Trong đó:

• \(s\): Quãng đường đi được (m)
• \(v_0\): Vận tốc ban đầu (m/s)
• \(a\): Gia tốc (m/s²)
• \(t\): Thời gian chuyển động (s)
• 3. Sau bao lâu ô tô đạt được vận tốc nhất định trong chuyển động thẳng nhanh dần đều?

Để tính thời gian cần thiết để ô tô đạt được vận tốc \(v\), ta sử dụng công thức:

\[ t = \frac{v - v_0}{a} \]

Trong đó:

• \(t\): Thời gian cần thiết (s)
• \(v\): Vận tốc cần đạt (m/s)
• \(v_0\): Vận tốc ban đầu (m/s)
• \(a\): Gia tốc (m/s²)
• 4. Ví dụ thực tế về chuyển động thẳng nhanh dần đều?

Ví dụ, một ô tô bắt đầu chuyển động từ trạng thái đứng yên với gia tốc không đổi là 0.5 m/s². Sau 10 giây, vận tốc của xe đạt 5 m/s và quãng đường xe đi được là:

\[ s = 0 \cdot 10 + \frac{1}{2} \cdot 0.5 \cdot 10^2 = 25 \, \text{m} \]

Vận tốc cuối cùng sau 10 giây là:

\[ v = 0 + 0.5 \cdot 10 = 5 \, \text{m/s} \]
• 5. Quãng đường có thay đổi khi tăng gia tốc không?

Có. Nếu gia tốc tăng, quãng đường đi được trong cùng khoảng thời gian sẽ tăng lên, vì gia tốc càng lớn thì vật chuyển động càng nhanh.