Chuyển động thẳng đều thì: Định nghĩa, Công thức và Ứng dụng Thực tiễn

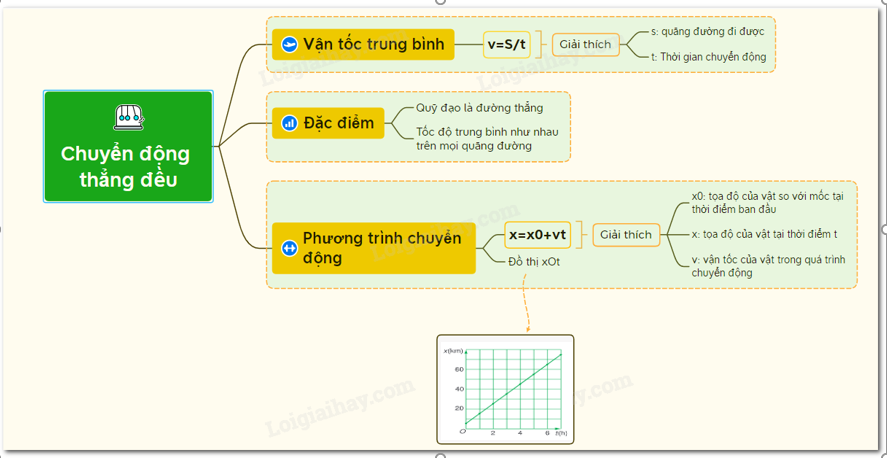
Chuyển động thẳng đều là chuyển động có quỹ đạo là một đường thẳng và vận tốc của vật không thay đổi theo thời gian. Điều này có nghĩa là vật di chuyển quãng đường bằng nhau trong các khoảng thời gian bằng nhau.

Phương trình chuyển động thẳng đều có dạng:

\[ x = x_0 + v \cdot t \]

• \( x_0 \) là tọa độ ban đầu của vật
• \( v \) là vận tốc của vật
• \( t \) là thời gian vật di chuyển

Trong chuyển động thẳng đều, quãng đường đi được \( s \) của vật được tính bằng công thức:

\[ s = v \cdot t \]

• \( v \) là vận tốc của vật
• \( t \) là thời gian vật di chuyển

Vận tốc trung bình \( v_{tb} \) của một vật trong chuyển động thẳng đều được xác định bằng:

\[ v_{tb} = \frac{s}{t} \]

• \( s \) là quãng đường vật đã di chuyển
• \( t \) là thời gian vật di chuyển

Đồ thị tọa độ theo thời gian của chuyển động thẳng đều là một đường thẳng, thể hiện sự phụ thuộc của tọa độ vào thời gian. Nếu vẽ đồ thị với trục hoành là thời gian và trục tung là tọa độ, đường thẳng này có độ dốc tương ứng với vận tốc của vật.

Ví dụ về đồ thị tọa độ - thời gian:

1. Một chiếc xe chuyển động thẳng đều với vận tốc \( 60 \, \text{km/h} \). Tính quãng đường xe đi được sau 3 giờ.

Giải:

\[ s = v \cdot t = 60 \cdot 3 = 180 \, \text{km} \]

2. Một vật chuyển động thẳng đều từ vị trí ban đầu có tọa độ \( 10 \, \text{m} \) với vận tốc \( 2 \, \text{m/s} \). Tính tọa độ của vật sau 5 giây.

Giải:

\[ x = x_0 + v \cdot t = 10 + 2 \cdot 5 = 20 \, \text{m} \]

Phương trình chuyển động thẳng đều có dạng:

\[ x = x_0 + v \cdot t \]

• \( x_0 \) là tọa độ ban đầu của vật
• \( v \) là vận tốc của vật
• \( t \) là thời gian vật di chuyển

Trong chuyển động thẳng đều, quãng đường đi được \( s \) của vật được tính bằng công thức:

\[ s = v \cdot t \]

• \( v \) là vận tốc của vật
• \( t \) là thời gian vật di chuyển

Vận tốc trung bình \( v_{tb} \) của một vật trong chuyển động thẳng đều được xác định bằng:

\[ v_{tb} = \frac{s}{t} \]

• \( s \) là quãng đường vật đã di chuyển
• \( t \) là thời gian vật di chuyển

Đồ thị tọa độ theo thời gian của chuyển động thẳng đều là một đường thẳng, thể hiện sự phụ thuộc của tọa độ vào thời gian. Nếu vẽ đồ thị với trục hoành là thời gian và trục tung là tọa độ, đường thẳng này có độ dốc tương ứng với vận tốc của vật.

Ví dụ về đồ thị tọa độ - thời gian:

1. Một chiếc xe chuyển động thẳng đều với vận tốc \( 60 \, \text{km/h} \). Tính quãng đường xe đi được sau 3 giờ.

Giải:

\[ s = v \cdot t = 60 \cdot 3 = 180 \, \text{km} \]

2. Một vật chuyển động thẳng đều từ vị trí ban đầu có tọa độ \( 10 \, \text{m} \) với vận tốc \( 2 \, \text{m/s} \). Tính tọa độ của vật sau 5 giây.

Giải:

\[ x = x_0 + v \cdot t = 10 + 2 \cdot 5 = 20 \, \text{m} \]

Trong chuyển động thẳng đều, quãng đường đi được \( s \) của vật được tính bằng công thức:

\[ s = v \cdot t \]

• \( v \) là vận tốc của vật
• \( t \) là thời gian vật di chuyển

Vận tốc trung bình \( v_{tb} \) của một vật trong chuyển động thẳng đều được xác định bằng:

\[ v_{tb} = \frac{s}{t} \]

• \( s \) là quãng đường vật đã di chuyển
• \( t \) là thời gian vật di chuyển

Đồ thị tọa độ theo thời gian của chuyển động thẳng đều là một đường thẳng, thể hiện sự phụ thuộc của tọa độ vào thời gian. Nếu vẽ đồ thị với trục hoành là thời gian và trục tung là tọa độ, đường thẳng này có độ dốc tương ứng với vận tốc của vật.

Ví dụ về đồ thị tọa độ - thời gian:

1. Một chiếc xe chuyển động thẳng đều với vận tốc \( 60 \, \text{km/h} \). Tính quãng đường xe đi được sau 3 giờ.

Giải:

\[ s = v \cdot t = 60 \cdot 3 = 180 \, \text{km} \]

2. Một vật chuyển động thẳng đều từ vị trí ban đầu có tọa độ \( 10 \, \text{m} \) với vận tốc \( 2 \, \text{m/s} \). Tính tọa độ của vật sau 5 giây.

Giải:

\[ x = x_0 + v \cdot t = 10 + 2 \cdot 5 = 20 \, \text{m} \]

Vận tốc trung bình \( v_{tb} \) của một vật trong chuyển động thẳng đều được xác định bằng:

\[ v_{tb} = \frac{s}{t} \]

• \( s \) là quãng đường vật đã di chuyển
• \( t \) là thời gian vật di chuyển

Đồ thị tọa độ theo thời gian của chuyển động thẳng đều là một đường thẳng, thể hiện sự phụ thuộc của tọa độ vào thời gian. Nếu vẽ đồ thị với trục hoành là thời gian và trục tung là tọa độ, đường thẳng này có độ dốc tương ứng với vận tốc của vật.

Ví dụ về đồ thị tọa độ - thời gian:

1. Một chiếc xe chuyển động thẳng đều với vận tốc \( 60 \, \text{km/h} \). Tính quãng đường xe đi được sau 3 giờ.

Giải:

\[ s = v \cdot t = 60 \cdot 3 = 180 \, \text{km} \]

2. Một vật chuyển động thẳng đều từ vị trí ban đầu có tọa độ \( 10 \, \text{m} \) với vận tốc \( 2 \, \text{m/s} \). Tính tọa độ của vật sau 5 giây.

Giải:

\[ x = x_0 + v \cdot t = 10 + 2 \cdot 5 = 20 \, \text{m} \]

Đồ thị tọa độ theo thời gian của chuyển động thẳng đều là một đường thẳng, thể hiện sự phụ thuộc của tọa độ vào thời gian. Nếu vẽ đồ thị với trục hoành là thời gian và trục tung là tọa độ, đường thẳng này có độ dốc tương ứng với vận tốc của vật.

Ví dụ về đồ thị tọa độ - thời gian:

1. Một chiếc xe chuyển động thẳng đều với vận tốc \( 60 \, \text{km/h} \). Tính quãng đường xe đi được sau 3 giờ.

Giải:

\[ s = v \cdot t = 60 \cdot 3 = 180 \, \text{km} \]

2. Một vật chuyển động thẳng đều từ vị trí ban đầu có tọa độ \( 10 \, \text{m} \) với vận tốc \( 2 \, \text{m/s} \). Tính tọa độ của vật sau 5 giây.

Giải:

\[ x = x_0 + v \cdot t = 10 + 2 \cdot 5 = 20 \, \text{m} \]

1. Một chiếc xe chuyển động thẳng đều với vận tốc \( 60 \, \text{km/h} \). Tính quãng đường xe đi được sau 3 giờ.

Giải:

\[ s = v \cdot t = 60 \cdot 3 = 180 \, \text{km} \]

2. Một vật chuyển động thẳng đều từ vị trí ban đầu có tọa độ \( 10 \, \text{m} \) với vận tốc \( 2 \, \text{m/s} \). Tính tọa độ của vật sau 5 giây.

Giải:

\[ x = x_0 + v \cdot t = 10 + 2 \cdot 5 = 20 \, \text{m} \]

Chuyển động thẳng đều là một dạng chuyển động của vật mà quỹ đạo là đường thẳng và vận tốc của vật không thay đổi theo thời gian. Đây là một trong những dạng chuyển động cơ bản nhất trong vật lý học và thường được đề cập đến ở cấp độ trung học cơ sở và phổ thông.

1. Định Nghĩa Chuyển Động Thẳng Đều

Chuyển động thẳng đều là chuyển động của một vật theo một đường thẳng với vận tốc không đổi. Trong chuyển động này, vật di chuyển quãng đường như nhau trong các khoảng thời gian bằng nhau. Đặc điểm quan trọng nhất của chuyển động thẳng đều là vận tốc không thay đổi và không có gia tốc tác động lên vật.

Phương trình tọa độ của chuyển động thẳng đều được biểu diễn bằng công thức:

\[ x = x_0 + v \cdot (t - t_0) \]

• \(x\): tọa độ của vật tại thời điểm \(t\).
• \(x_0\): tọa độ ban đầu của vật tại thời điểm \(t_0\).
• \(v\): vận tốc không đổi của vật.
• \(t\): thời gian đã trôi qua từ thời điểm ban đầu \(t_0\).

2. Đặc Điểm Của Chuyển Động Thẳng Đều

• Quỹ đạo: Quỹ đạo của chuyển động thẳng đều là một đường thẳng.
• Vận tốc: Vận tốc của vật là không đổi theo thời gian, tức là vận tốc có độ lớn và hướng không thay đổi.
• Gia tốc: Trong chuyển động thẳng đều, gia tốc của vật bằng 0 vì vận tốc không thay đổi.
• Quãng đường: Quãng đường đi được của vật tỷ lệ thuận với thời gian chuyển động, được tính bằng công thức: \[ s = v \cdot t \]

Chuyển động thẳng đều là nền tảng cơ bản giúp học sinh hiểu rõ hơn về các loại chuyển động khác và là bước khởi đầu quan trọng để tiếp cận với các khái niệm phức tạp hơn trong cơ học.

Chuyển động thẳng đều là chuyển động có quỹ đạo là đường thẳng, và tốc độ trung bình của vật luôn không đổi trên mọi quãng đường. Để hiểu rõ hơn về chuyển động thẳng đều, chúng ta cần nắm vững các công thức và phương trình liên quan đến loại chuyển động này.

• Tốc độ trung bình: Tốc độ trung bình là đại lượng đặc trưng cho mức độ nhanh hay chậm của chuyển động, được tính bằng thương số giữa quãng đường đi được và thời gian để đi hết quãng đường đó.
• Biểu thức tốc độ trung bình: \[ v_{tb} = \frac{s}{t} \]
  • Trong đó:
    • \(s\): Quãng đường đi được (mét, km, ...).
    • \(t\): Thời gian đi hết quãng đường (giây, phút, ...).
• Phương trình chuyển động thẳng đều: Phương trình mô tả vị trí của vật theo thời gian khi vật chuyển động thẳng đều. \[ x = x_0 + vt \]
  • Trong đó:
    • \(x\): Tọa độ của vật tại thời điểm \(t\) (m).
    • \(x_0\): Tọa độ ban đầu của vật (m).
    • \(v\): Vận tốc của vật (m/s).
    • \(t\): Thời gian chuyển động (s).

Đồ thị tọa độ - thời gian của chuyển động thẳng đều là một đường thẳng có độ dốc bằng vận tốc \(v\). Độ dốc này càng lớn khi vận tốc càng cao, cho thấy mối liên hệ trực tiếp giữa quãng đường đi được và thời gian di chuyển.

Chuyển động thẳng đều là nền tảng cho nhiều hiện tượng vật lý và bài toán trong thực tế, do đó, việc hiểu rõ công thức và phương trình của chuyển động này sẽ giúp bạn giải quyết các bài tập hiệu quả hơn.

Chuyển động thẳng đều không chỉ là một khái niệm lý thuyết mà còn có rất nhiều ứng dụng thực tế trong cuộc sống và khoa học. Dưới đây là một số ví dụ minh họa giúp làm rõ hơn về ứng dụng của chuyển động thẳng đều.

• Ứng Dụng Trong Cuộc Sống Hằng Ngày:
  • Chuyển động của xe hơi trên một đoạn đường thẳng với tốc độ không đổi.
  • Máy bay duy trì tốc độ đều khi bay trong điều kiện ổn định.
  • Chuyển động thẳng đều của băng chuyền trong các nhà máy sản xuất.
• Bài Tập Minh Họa:
  1. Giả sử một xe hơi chuyển động thẳng đều với vận tốc \(v = 60 \, \text{km/h}\). Tính quãng đường mà xe đi được sau \(t = 2 \, \text{h}\).

  Giải: Áp dụng công thức chuyển động thẳng đều \(S = v \cdot t\):

  \[ S = 60 \times 2 = 120 \, \text{km} \]
  2. Một người đi bộ với vận tốc \(v = 5 \, \text{km/h}\) trong 3 giờ trên một con đường thẳng. Tính quãng đường người đó đã đi được.

  Giải: Áp dụng công thức chuyển động thẳng đều \(S = v \cdot t\):

  \[ S = 5 \times 3 = 15 \, \text{km} \]

Những ví dụ này giúp củng cố kiến thức về chuyển động thẳng đều, từ đó nâng cao khả năng áp dụng vào thực tế và làm tốt các bài kiểm tra liên quan.

Chuyển động thẳng đều là một trong những kiến thức cơ bản của vật lý, nhưng để hiểu sâu hơn, chúng ta cần khám phá các khái niệm liên quan và mở rộng ứng dụng trong nhiều lĩnh vực khác nhau. Dưới đây là một số khái niệm và nội dung mở rộng cần nắm vững.

• 1. Khái niệm Vectơ Tốc Độ và Tốc Độ Tuyệt Đối:
  • Vectơ tốc độ là một đại lượng véc tơ đặc trưng cho sự chuyển động của vật. Nó có độ lớn bằng tốc độ và hướng của chuyển động.
  • Tốc độ tuyệt đối là độ lớn của vectơ tốc độ và không mang tính chiều.
• 2. Khái Niệm Về Hệ Tham Chiếu:
  • Hệ tham chiếu là một hệ tọa độ được sử dụng để xác định vị trí của một điểm trong không gian và thời gian.
  • Chuyển động của vật có thể được mô tả khác nhau tùy thuộc vào hệ tham chiếu được chọn.
• 3. Các Loại Chuyển Động Khác Liên Quan:
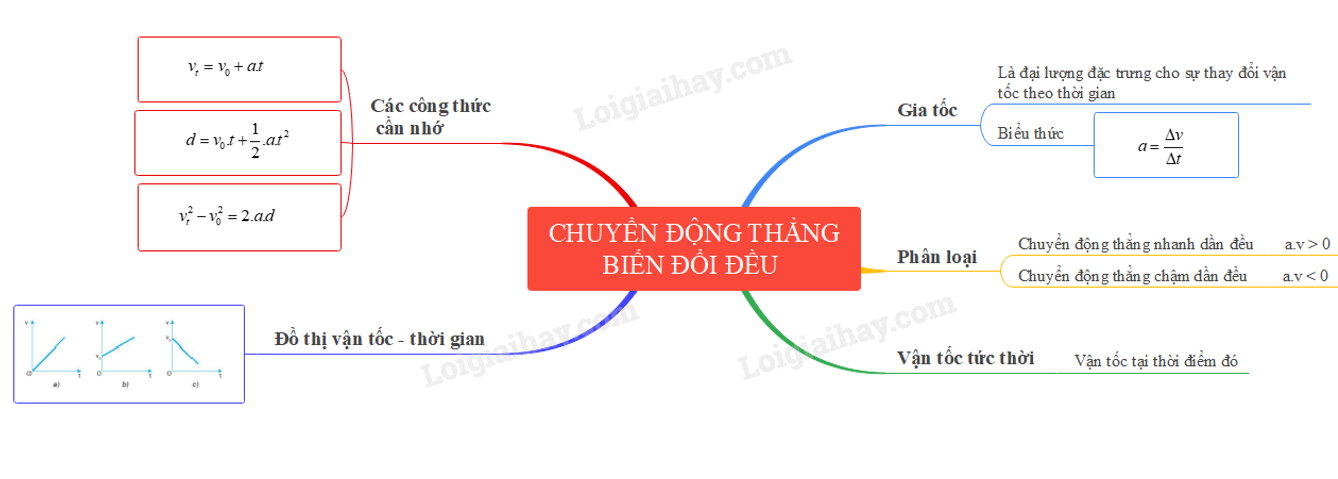
  1. Chuyển động thẳng biến đổi đều: Chuyển động với gia tốc không đổi, tốc độ thay đổi theo thời gian.
  2. Chuyển động tròn đều: Vật chuyển động theo đường tròn với tốc độ không đổi.
  3. Chuyển động dao động: Vật chuyển động lặp đi lặp lại quanh một vị trí cân bằng.
• 4. Liên Hệ Giữa Các Khái Niệm Vật Lý Khác:
  • Mối quan hệ giữa vận tốc và gia tốc trong chuyển động thẳng biến đổi đều.
  • Liên hệ giữa chuyển động thẳng đều và định luật Newton thứ nhất.
• 5. Ứng Dụng Kiến Thức Chuyển Động Trong Đời Sống và Kỹ Thuật:
  • Sử dụng công nghệ GPS để xác định vận tốc và vị trí của các phương tiện di chuyển.
  • Áp dụng nguyên lý chuyển động thẳng đều trong thiết kế băng chuyền và hệ thống di chuyển tự động.

Những kiến thức mở rộng này giúp chúng ta nắm rõ hơn về bản chất của chuyển động thẳng đều, từ đó áp dụng vào việc giải các bài tập phức tạp hơn và trong các lĩnh vực ứng dụng thực tế khác nhau.

Trong chuyển động thẳng đều, các dạng bài tập thường gặp rất đa dạng và yêu cầu sử dụng các công thức và phương trình đã học để giải quyết. Dưới đây là một số dạng bài tập tiêu biểu và phương pháp giải tương ứng:

1. Dạng 1: Tính vận tốc trung bình
   • Bài toán: Một xe di chuyển trong hai giai đoạn với hai vận tốc khác nhau. Tính vận tốc trung bình trên toàn bộ hành trình.
   • Phương pháp giải:

     
     - Giả sử xe di chuyển trong khoảng thời gian \( t_1 \) với vận tốc \( v_1 \) và trong khoảng thời gian \( t_2 \) với vận tốc \( v_2 \). Tính quãng đường đi được trong từng giai đoạn:
     \[ S_1 = v_1 \cdot t_1, \quad S_2 = v_2 \cdot t_2 \]
     - Tính tổng quãng đường \( S = S_1 + S_2 \) và tổng thời gian \( T = t_1 + t_2 \).
     - Vận tốc trung bình \( v_{tb} \) được tính bằng:
     \[ v_{tb} = \frac{S}{T} = \frac{S_1 + S_2}{t_1 + t_2} \]

2. Dạng 2: Lập phương trình chuyển động của các vật
   • Bài toán: Hai xe khởi hành từ hai điểm khác nhau và chuyển động với các vận tốc khác nhau trên cùng một đường thẳng. Lập phương trình chuyển động cho mỗi xe và tìm điểm gặp nhau.
   • Phương pháp giải:

     
     - Đặt gốc tọa độ tại điểm xuất phát của một trong hai xe, chọn chiều dương là chiều chuyển động của xe đó.
     
     - Phương trình chuyển động cho xe thứ nhất có dạng:
     \[ x_1 = x_{01} + v_1 \cdot t \]
     với \( x_{01} \) là vị trí ban đầu và \( v_1 \) là vận tốc của xe.
     
     - Tương tự, phương trình chuyển động cho xe thứ hai là:
     \[ x_2 = x_{02} + v_2 \cdot t \]
     - Để tìm thời điểm gặp nhau, giải phương trình \( x_1 = x_2 \).

3. Dạng 3: Bài tập đồ thị tọa độ - thời gian
   • Bài toán: Vẽ đồ thị tọa độ - thời gian của hai vật chuyển động thẳng đều và xác định điểm giao nhau trên đồ thị.
   • Phương pháp giải:

     
     - Xác định phương trình chuyển động cho mỗi vật dựa trên điều kiện ban đầu.
     
     - Sử dụng phương trình \( x = x_0 + vt \) để vẽ đồ thị.
     
     - Tìm giao điểm của hai đồ thị để xác định thời điểm và vị trí hai vật gặp nhau.

4. Dạng 4: Tính quãng đường đi được trong một khoảng thời gian
   • Bài toán: Một vật chuyển động thẳng đều từ vị trí A đến B trong khoảng thời gian t. Tính quãng đường đi được trong khoảng thời gian đã cho.
   • Phương pháp giải:

     
     - Sử dụng công thức quãng đường:
     \[ S = v \cdot t \]
     với \( v \) là vận tốc và \( t \) là thời gian di chuyển.

Với các dạng bài tập trên, việc nắm vững lý thuyết và công thức cơ bản là chìa khóa để giải quyết các bài toán về chuyển động thẳng đều một cách hiệu quả.

Để ôn luyện và củng cố kiến thức về chuyển động thẳng đều, học sinh cần thực hiện các bài tập đa dạng từ cơ bản đến nâng cao. Việc luyện tập sẽ giúp học sinh nắm vững lý thuyết, áp dụng chính xác các công thức, và hiểu rõ hơn về các dạng bài tập thường gặp. Dưới đây là một số đề thi thử và bài tập luyện tập nhằm hỗ trợ học sinh chuẩn bị tốt cho các kỳ thi.

• Đề thi thử môn Vật lý lớp 10:

  1. Đề thi số 1: Tính toán vận tốc trung bình và quãng đường trong chuyển động thẳng đều của một ô tô trên đoạn đường thẳng.

  2. Đề thi số 2: Viết phương trình chuyển động của một vật di chuyển thẳng đều và xác định vị trí của vật sau một khoảng thời gian cho trước.

• Bài tập luyện tập:

  1. Dạng bài tập 1: Xác định vận tốc trung bình và quãng đường của một vật trong chuyển động thẳng đều.

  2. Dạng bài tập 2: Viết phương trình chuyển động và tìm thời điểm hai vật gặp nhau.

  3. Dạng bài tập 3: Ứng dụng các công thức tính quãng đường, vận tốc để giải các bài toán thực tế.

• Câu hỏi trắc nghiệm:

  1. Câu hỏi 1: Khi một vật chuyển động thẳng đều, đại lượng nào dưới đây không thay đổi? A) Vận tốc B) Quãng đường C) Thời gian

  2. Câu hỏi 2: Một vật di chuyển với vận tốc không đổi 20 km/h trong 3 giờ. Tính quãng đường mà vật đã đi được.

Học sinh có thể tham khảo thêm các nguồn tài liệu và đề thi mẫu để nâng cao kỹ năng giải bài tập và tự tin hơn khi bước vào các kỳ thi thực tế.

Chuyển động thẳng đều là một khái niệm cơ bản trong vật lý, thể hiện sự di chuyển của vật với vận tốc không đổi trên một đường thẳng. Hiểu rõ đặc điểm và công thức của chuyển động thẳng đều giúp học sinh nắm bắt được bản chất của chuyển động trong tự nhiên, từ đó có thể áp dụng vào các bài tập và thực tế.

Qua các phần đã trình bày, chúng ta đã khám phá từ định nghĩa, công thức, phương trình đến các ứng dụng và bài tập minh họa liên quan đến chuyển động thẳng đều. Điều này không chỉ giúp củng cố kiến thức mà còn tạo cơ hội để học sinh thực hành và áp dụng vào những tình huống thực tế. Hơn nữa, việc tìm hiểu về các khái niệm liên quan và mở rộng thêm kiến thức giúp chúng ta có cái nhìn toàn diện hơn về chủ đề này.

• Định nghĩa và đặc điểm: Làm rõ các yếu tố cơ bản về chuyển động thẳng đều và các đại lượng vật lý liên quan.

• Công thức và phương trình: Cung cấp các công thức tính toán quan trọng, giúp giải quyết các bài toán liên quan đến chuyển động thẳng đều.

• Ứng dụng và bài tập: Đưa ra các ví dụ thực tế và bài tập minh họa để học sinh dễ dàng áp dụng kiến thức vào thực hành.

• Kiến thức mở rộng: Liên hệ chuyển động thẳng đều với các khái niệm vật lý khác, tạo nền tảng để hiểu sâu hơn về cơ học.

• Ôn tập và luyện tập: Đề xuất các dạng bài tập và đề thi thử để học sinh có thể tự kiểm tra và củng cố kiến thức.

Kết luận, việc nắm vững kiến thức về chuyển động thẳng đều không chỉ giúp học sinh đạt kết quả cao trong học tập mà còn ứng dụng hiệu quả vào đời sống. Hãy tiếp tục luyện tập và khám phá thêm những khía cạnh khác của vật lý để nâng cao tư duy khoa học và kỹ năng giải quyết vấn đề.