Chủ đề xác định số electron thừa thiếu ở mỗi quả cầu: Xác định số electron thừa thiếu ở mỗi quả cầu là một bài toán quan trọng trong vật lý, giúp hiểu rõ hơn về các nguyên lý điện tích và tương tác giữa các vật thể mang điện. Bài viết này cung cấp phương pháp chi tiết và bài tập minh họa thực tiễn, hỗ trợ học sinh và người học nắm vững kiến thức một cách dễ dàng.
Mục lục
Xác định số electron thừa thiếu ở mỗi quả cầu
Trong lĩnh vực vật lý, đặc biệt là ở cấp học lớp 11, bài toán xác định số electron thừa thiếu ở mỗi quả cầu là một dạng bài tập quan trọng. Bài toán này giúp học sinh hiểu rõ hơn về thuyết electron, điện tích và các tương tác giữa các vật thể mang điện.
Khái niệm cơ bản
Mỗi quả cầu mang điện có thể thừa hoặc thiếu electron so với trạng thái trung hòa điện tích. Khi hai quả cầu tiếp xúc với nhau, các electron có thể di chuyển giữa chúng, dẫn đến thay đổi điện tích trên mỗi quả cầu. Việc xác định số electron thừa thiếu sau khi tiếp xúc giúp học sinh nắm vững các nguyên lý của định luật bảo toàn điện tích và tương tác tĩnh điện.
Phương pháp tính toán
Để xác định số electron thừa thiếu ở mỗi quả cầu, ta thường thực hiện theo các bước sau:
- Xác định điện tích ban đầu của mỗi quả cầu, thường ký hiệu là \(q_1\) và \(q_2\).
- Tính toán số electron tương ứng với mỗi điện tích theo công thức: \[ N = \frac{|q|}{e} \] trong đó \(q\) là điện tích của quả cầu, và \(e\) là điện tích của một electron (khoảng \(1.6 \times 10^{-19}\) Coulomb).
- Sau khi cho hai quả cầu tiếp xúc, điện tích của chúng có thể thay đổi. Ta cần xác định lại điện tích mới \(q_1'\) và \(q_2'\).
- Dựa trên điện tích mới, xác định lại số electron trên mỗi quả cầu sau khi tiếp xúc.
Ví dụ minh họa
Giả sử hai quả cầu kim loại nhỏ A và B, với điện tích ban đầu lần lượt là \(q_1 = -3.2 \times 10^{-7}\) C và \(q_2 = 2.4 \times 10^{-7}\) C, được đặt cách nhau 12 cm trong không khí. Sau khi cho hai quả cầu tiếp xúc với nhau và tách ra, điện tích mới của mỗi quả cầu có thể được tính như sau:
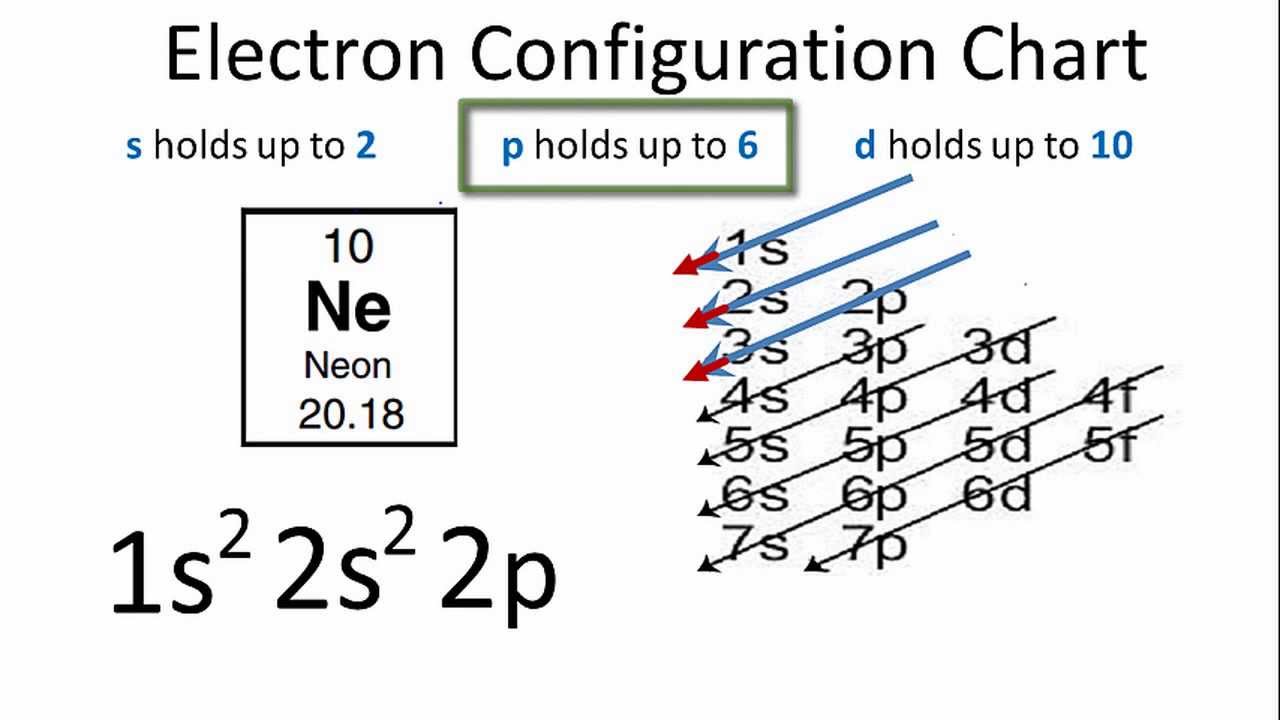
- Số electron thừa ở quả cầu A: \(N_1 = \frac{q_1}{e} = \frac{-3.2 \times 10^{-7}}{1.6 \times 10^{-19}} = 2 \times 10^{12}\) electron.
- Số electron thiếu ở quả cầu B: \(N_2 = \frac{q_2}{e} = \frac{2.4 \times 10^{-7}}{1.6 \times 10^{-19}} = 1.5 \times 10^{12}\) electron.
Sau khi tiếp xúc, điện tích của hai quả cầu sẽ bằng nhau và bằng trung bình cộng của hai điện tích ban đầu. Từ đó, ta có thể xác định lại số electron thừa thiếu tương ứng.
Kết luận
Qua các bài toán như vậy, học sinh không chỉ nắm vững lý thuyết mà còn phát triển khả năng tư duy logic và áp dụng kiến thức vào giải quyết các vấn đề thực tiễn. Đây là một phần không thể thiếu trong chương trình học vật lý lớp 11.
.png)
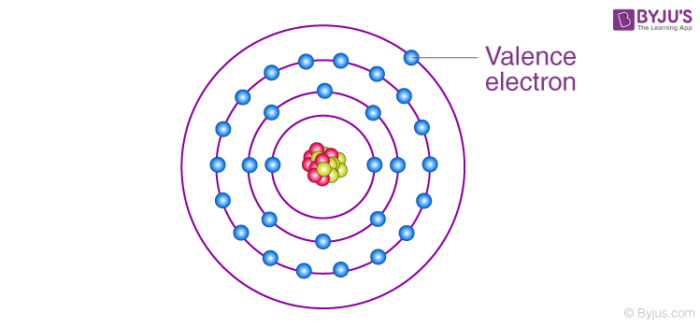
Giới thiệu về khái niệm điện tích và electron
Điện tích và electron là hai khái niệm cơ bản trong vật lý học, đặc biệt quan trọng trong lĩnh vực điện học. Điện tích là một đại lượng vật lý thể hiện khả năng của một vật thể trong việc tương tác với các vật thể khác thông qua lực điện từ. Điện tích được chia thành hai loại chính: điện tích dương và điện tích âm.
Electron là một hạt cơ bản mang điện tích âm, và nó là thành phần chính tạo nên dòng điện trong các vật dẫn. Trong một nguyên tử, electron di chuyển quanh hạt nhân và có vai trò quan trọng trong việc tạo ra các liên kết hóa học cũng như trong các hiện tượng điện từ.
Khi hai vật mang điện tích khác nhau tiếp xúc, các electron có thể di chuyển từ vật này sang vật khác, dẫn đến sự thay đổi điện tích trên mỗi vật. Điều này có thể được biểu diễn qua công thức:
\[
q = n \times e
\]
Trong đó:
- \(q\) là điện tích của vật (đo bằng Coulomb)
- \(n\) là số lượng electron
- \(e\) là điện tích của một electron, với giá trị tuyệt đối là \(1.6 \times 10^{-19}\) Coulomb
Hiểu rõ về điện tích và electron là bước đầu tiên để nắm vững các hiện tượng điện từ và cách chúng ảnh hưởng đến môi trường xung quanh.
Phương pháp xác định số electron thừa thiếu
Để xác định số electron thừa hoặc thiếu trên mỗi quả cầu sau khi tiếp xúc với nhau, chúng ta cần tuân theo một quy trình cụ thể. Quá trình này dựa trên các nguyên tắc vật lý liên quan đến điện tích và sự bảo toàn điện tích. Dưới đây là các bước cơ bản để thực hiện:
-
Bước 1: Xác định điện tích ban đầu của mỗi quả cầu
Trước tiên, ta cần xác định điện tích ban đầu của mỗi quả cầu, được ký hiệu là \(q_1\) và \(q_2\). Điện tích này có thể được biết trước hoặc tính toán dựa trên các điều kiện ban đầu.
-
Bước 2: Xác định tổng điện tích
Tiếp theo, tính tổng điện tích của hệ gồm hai quả cầu bằng cách cộng điện tích của từng quả cầu:
\[
q_{\text{total}} = q_1 + q_2
\]Điều này dựa trên định luật bảo toàn điện tích, tức là tổng điện tích trong hệ thống không đổi trước và sau khi hai quả cầu tiếp xúc.
-
Bước 3: Xác định điện tích sau khi hai quả cầu tiếp xúc
Sau khi hai quả cầu tiếp xúc, điện tích của chúng sẽ phân bố lại sao cho cả hai quả cầu đều có cùng điện tích. Điện tích mới trên mỗi quả cầu được tính bằng công thức:
\[
q' = \frac{q_{\text{total}}}{2}
\] -
Bước 4: Tính số electron thừa hoặc thiếu
Sau khi biết được điện tích mới \(q'\) trên mỗi quả cầu, chúng ta có thể tính số electron thừa hoặc thiếu bằng công thức:
\[
N = \frac{|q'|}{e}
\]Trong đó, \(e\) là điện tích của một electron, với giá trị khoảng \(1.6 \times 10^{-19}\) Coulomb.
Bằng cách thực hiện các bước trên, chúng ta có thể dễ dàng xác định được số lượng electron thừa hoặc thiếu trên mỗi quả cầu sau khi chúng tương tác với nhau. Phương pháp này là một phần quan trọng trong việc hiểu rõ hơn về các hiện tượng điện từ và các nguyên lý bảo toàn trong vật lý.

Bài tập minh họa về xác định số electron thừa thiếu
Dưới đây là một số bài tập minh họa để giúp bạn hiểu rõ hơn về cách xác định số electron thừa thiếu ở mỗi quả cầu và cách tính toán liên quan đến điện tích:
Ví dụ 1: Xác định số electron thừa thiếu ở hai quả cầu
Giả sử hai quả cầu kim loại nhỏ A và B đặt trong không khí, có điện tích lần lượt là \( q_1 = -3,2 \times 10^{-7} \, C \) và \( q_2 = 2,4 \times 10^{-7} \, C \), cách nhau một khoảng 12 cm. Hãy xác định số electron thừa hoặc thiếu ở mỗi quả cầu.
Giải:
- Điện tích của electron là \( e = 1,6 \times 10^{-19} \, C \).
- Số electron thừa ở quả cầu A được tính bằng công thức: \[ N_1 = \frac{|q_1|}{e} = \frac{3,2 \times 10^{-7} \, C}{1,6 \times 10^{-19} \, C/e} = 2 \times 10^{12} \, \text{electron}. \]
- Số electron thiếu ở quả cầu B được tính bằng công thức: \[ N_2 = \frac{q_2}{e} = \frac{2,4 \times 10^{-7} \, C}{1,6 \times 10^{-19} \, C/e} = 1,5 \times 10^{12} \, \text{electron}. \]
Ví dụ 2: Tính lực tương tác giữa hai quả cầu
Sau khi đã xác định số electron thừa và thiếu ở mỗi quả cầu, bạn có thể tính lực tương tác điện giữa chúng bằng định luật Coulomb:
Giải:
Lực tương tác điện giữa hai quả cầu là lực hút, được tính theo công thức:
với \( k = 9 \times 10^9 \, N \cdot m^2 / C^2 \), \( r = 0,12 \, m \).
Thay các giá trị vào, ta có:
Ví dụ 3: Tương tác sau khi tiếp xúc
Cho hai quả cầu tiếp xúc với nhau rồi đặt về vị trí cũ, hãy tính lực tương tác điện giữa chúng sau khi tiếp xúc.
Giải:
- Khi tiếp xúc, điện tích sẽ phân bố đều trên cả hai quả cầu, do đó điện tích mới của mỗi quả cầu là: \[ q' = \frac{q_1 + q_2}{2} = \frac{-3,2 \times 10^{-7} + 2,4 \times 10^{-7}}{2} = -0,4 \times 10^{-7} \, C. \]
- Lực tương tác sau khi tiếp xúc là: \[ F' = 9 \times 10^9 \times \frac{(0,4 \times 10^{-7})^2}{(0,12)^2} = 10^{-3} \, N. \]

Các trường hợp đặc biệt khi xác định số electron
Khi xác định số lượng electron thừa hoặc thiếu ở các quả cầu, có một số trường hợp đặc biệt cần lưu ý để đảm bảo tính chính xác trong tính toán và lý thuyết:
1. Ảnh hưởng của môi trường xung quanh
Điện tích và sự phân bố của electron trên các quả cầu có thể bị ảnh hưởng bởi môi trường xung quanh, chẳng hạn như không khí, chất lỏng hay điện môi. Môi trường này có thể thay đổi lực tương tác giữa các điện tích, dẫn đến sự thay đổi trong số lượng electron cần thiết để cân bằng hệ thống.
Ví dụ, khi hai quả cầu mang điện tích được đặt trong không khí, lực tương tác giữa chúng sẽ khác so với khi đặt trong dầu. Trong môi trường điện môi, hằng số điện môi của chất lỏng sẽ ảnh hưởng đến lực tương tác, từ đó ảnh hưởng đến số lượng electron thừa hoặc thiếu cần tính toán.
2. Tác động của khoảng cách giữa các quả cầu
Khoảng cách giữa các quả cầu cũng đóng vai trò quan trọng trong việc xác định số lượng electron. Theo định luật Coulomb, lực tương tác giữa hai điện tích tỉ lệ nghịch với bình phương khoảng cách giữa chúng. Khi khoảng cách thay đổi, lực tương tác cũng thay đổi, dẫn đến việc số electron cần để duy trì cân bằng tĩnh điện cũng khác nhau.
Nếu hai quả cầu tiến lại gần nhau, lực tương tác tăng lên, có thể dẫn đến việc chuyển đổi electron từ quả cầu này sang quả cầu kia để duy trì cân bằng. Ngược lại, nếu khoảng cách tăng lên, lực tương tác giảm đi và số lượng electron cần thiết cũng có thể giảm theo.
3. Hiện tượng phân bố không đều của điện tích
Trong một số trường hợp, điện tích không phân bố đều trên bề mặt của quả cầu, điều này có thể do hình dạng đặc biệt của vật thể hoặc do sự phân bố không đồng đều của các điện tích ban đầu. Khi điện tích không phân bố đều, việc tính toán số electron thừa thiếu cần phải xem xét đến mật độ điện tích tại từng điểm trên bề mặt quả cầu.
Chẳng hạn, nếu một quả cầu có mật độ điện tích cao hơn ở một đầu so với đầu kia, số electron cần thiết để cân bằng điện tích sẽ không giống như khi điện tích được phân bố đều. Trong trường hợp này, ta cần tích phân mật độ điện tích trên toàn bộ bề mặt quả cầu để xác định tổng số electron.
4. Trường hợp điện tích nằm trên các bề mặt khác nhau
Nếu điện tích không chỉ nằm trên một bề mặt mà được phân bố trên nhiều bề mặt khác nhau của vật thể, ta phải xem xét sự tương tác giữa các bề mặt này khi xác định số electron. Trong các trường hợp này, việc sử dụng các công thức tính mật độ điện tích như mật độ điện mặt \( \sigma \), mật độ điện dài \( \lambda \), và mật độ điện khối \( \rho \) là cần thiết để có được kết quả chính xác.
Những trường hợp đặc biệt này nhấn mạnh sự phức tạp của việc xác định số lượng electron thừa thiếu trong các hệ thống điện tích, yêu cầu phải có sự hiểu biết sâu sắc về vật lý và các hiện tượng tĩnh điện.