Quy tắc hợp lực song song ngược chiều: Khám phá toàn diện và ứng dụng thực tế

Quy tắc hợp lực song song ngược chiều là một trong những khái niệm cơ bản trong Vật lý, thường được giới thiệu ở cấp độ trung học phổ thông. Quy tắc này mô tả cách tổng hợp hai lực song song nhưng ngược chiều tác động lên một vật thể. Dưới đây là nội dung chi tiết về quy tắc này:

1. Định nghĩa

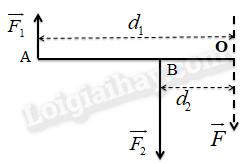
Khi hai lực \( \vec{F_1} \) và \( \vec{F_2} \) là hai lực song song nhưng ngược chiều tác dụng lên một vật rắn, hợp lực của chúng cũng sẽ là một lực song song với hai lực thành phần nhưng có chiều cùng với lực lớn hơn và độ lớn của hợp lực được tính bằng hiệu số độ lớn của hai lực đó.

Công thức xác định hợp lực:

\[
F = |F_1 - F_2|
\]

Với:

• \( F_1 \) là độ lớn của lực thứ nhất.
• \( F_2 \) là độ lớn của lực thứ hai.

2. Vị trí của hợp lực

Giá của hợp lực \( \vec{F} \) nằm trên đoạn thẳng nối hai điểm đặt của hai lực thành phần. Vị trí của hợp lực chia đoạn thẳng nối hai điểm đặt lực theo tỉ lệ nghịch với độ lớn của hai lực.

Công thức vị trí:

\[
\frac{d_2}{d_1} = \frac{F_1}{F_2}
\]

Với:

• \( d_1 \) là khoảng cách từ điểm đặt của lực \( F_1 \) đến vị trí của hợp lực \( \vec{F} \).
• \( d_2 \) là khoảng cách từ điểm đặt của lực \( F_2 \) đến vị trí của hợp lực \( \vec{F} \).

3. Ứng dụng thực tế

Quy tắc này được ứng dụng trong nhiều lĩnh vực thực tiễn như kỹ thuật xây dựng, cơ khí, và các lĩnh vực nghiên cứu vật lý khác. Việc hiểu và áp dụng đúng quy tắc này giúp tối ưu hóa sự ổn định và cân bằng của các hệ thống chịu lực trong thực tế.

4. Ví dụ minh họa

Hãy xét một thanh ngang chịu hai lực song song ngược chiều với \( F_1 = 100 \, \text{N} \) và \( F_2 = 60 \, \text{N} \) tác dụng. Giả sử khoảng cách giữa hai điểm đặt lực là 2 mét.

Theo công thức, hợp lực sẽ có độ lớn:

\[
F = 100 \, \text{N} - 60 \, \text{N} = 40 \, \text{N}
\]

Và vị trí của hợp lực cách điểm đặt của lực \( F_1 \) là:

\[
d_1 = \frac{60 \times 2}{100 + 60} = 0.75 \, \text{m}
\]

Kết quả này cho thấy hợp lực có chiều cùng chiều với lực lớn hơn (lực 100 N) và cách điểm đặt của nó 0.75 mét.

Quy tắc hợp lực song song ngược chiều là một nguyên tắc cơ bản trong vật lý học, thường được giảng dạy ở cấp trung học phổ thông. Nguyên tắc này đề cập đến việc tổng hợp hai lực song song nhưng có chiều ngược nhau tác động lên một vật thể. Đặc điểm của các lực này là mặc dù chúng nằm song song, nhưng chúng có xu hướng kéo vật theo các hướng đối lập, gây ra một hợp lực với đặc trưng riêng biệt.

Khi hai lực \(\vec{F_1}\) và \(\vec{F_2}\) tác động ngược chiều trên một vật, hợp lực sẽ được tính bằng hiệu số của độ lớn hai lực đó:

\[
F = |F_1 - F_2|
\]

Vị trí của hợp lực này sẽ nằm trên đoạn thẳng nối hai điểm đặt của hai lực và chia đoạn thẳng này theo tỷ lệ nghịch với độ lớn của các lực:

\[
\frac{d_2}{d_1} = \frac{F_1}{F_2}
\]

Trong đó:

• \(d_1\) là khoảng cách từ điểm đặt của lực \(F_1\) đến vị trí của hợp lực.
• \(d_2\) là khoảng cách từ điểm đặt của lực \(F_2\) đến vị trí của hợp lực.

Quy tắc này không chỉ giúp giải thích sự cân bằng của vật thể trong các bài toán lý thuyết mà còn có ứng dụng thực tế trong việc tính toán và thiết kế các hệ thống cơ học, nơi các lực tác động theo các hướng khác nhau cần được phân tích và quản lý một cách chính xác.

Khi hai lực song song nhưng ngược chiều tác dụng lên một vật, hợp lực của chúng sẽ có đặc điểm và vị trí được xác định bằng các công thức cụ thể. Để tính toán hợp lực này, chúng ta cần làm theo các bước sau:

1. Tính độ lớn của hợp lực:

   Độ lớn của hợp lực \( F \) được xác định bằng hiệu số tuyệt đối của độ lớn hai lực thành phần:

   \[
   F = |F_1 - F_2|
   \]

   Trong đó:

   • \( F_1 \) là độ lớn của lực thứ nhất.
   • \( F_2 \) là độ lớn của lực thứ hai.
2. Xác định vị trí của hợp lực:

   Vị trí của hợp lực \( F \) nằm trên đoạn thẳng nối hai điểm đặt của hai lực \( F_1 \) và \( F_2 \). Điểm đặt của hợp lực chia đoạn thẳng nối hai lực thành hai phần tỉ lệ nghịch với độ lớn của hai lực:

   \[
   \frac{d_2}{d_1} = \frac{F_1}{F_2}
   \]

   Với:

   • \( d_1 \) là khoảng cách từ điểm đặt của lực \( F_1 \) đến vị trí của hợp lực \( F \).
   • \{d_2\} là khoảng cách từ điểm đặt của lực \( F_2 \) đến vị trí của hợp lực \( F \).

Quá trình này giúp xác định không chỉ độ lớn của hợp lực mà còn vị trí tác dụng của nó, từ đó giúp phân tích và giải quyết các bài toán liên quan đến cân bằng lực một cách hiệu quả và chính xác.

Quy tắc hợp lực song song ngược chiều không chỉ là một khái niệm lý thuyết trong vật lý mà còn có nhiều ứng dụng quan trọng trong thực tế. Dưới đây là một số lĩnh vực và ví dụ cụ thể về cách quy tắc này được áp dụng:

1. Kỹ thuật xây dựng:

   Trong xây dựng, việc thiết kế và bố trí các thanh giằng, cột, và dầm thường yêu cầu phải tính toán chính xác các lực tác động lên chúng. Quy tắc hợp lực song song ngược chiều được áp dụng để đảm bảo sự cân bằng của các cấu trúc, đặc biệt là khi có hai lực đối nghịch tác động lên một thanh hoặc dầm.

2. Cơ khí và chế tạo:

   Trong lĩnh vực cơ khí, quy tắc này được sử dụng để thiết kế các chi tiết máy móc, đảm bảo rằng các bộ phận chịu lực có thể hoạt động bền bỉ mà không bị biến dạng hoặc hư hỏng. Ví dụ, khi thiết kế các trục quay hoặc bánh răng, các kỹ sư phải tính toán hợp lực để đảm bảo sự ổn định của hệ thống.

3. Thiết kế cầu và các công trình chịu tải:

   Trong các công trình cầu đường, việc sử dụng quy tắc hợp lực song song ngược chiều giúp xác định các điểm yếu và đảm bảo sự an toàn cho toàn bộ công trình. Các lực tác động từ xe cộ hoặc môi trường lên cầu đều phải được cân nhắc kỹ lưỡng.

4. Điện lực và hệ thống treo:

   Trong các hệ thống điện và cơ học, như hệ thống treo của ô tô hoặc các đường dây điện cao thế, quy tắc này giúp xác định lực căng và lực nén, đảm bảo các thành phần của hệ thống được bố trí và kết nối một cách hợp lý.

Như vậy, quy tắc hợp lực song song ngược chiều đóng vai trò quan trọng trong việc thiết kế, xây dựng và duy trì các hệ thống kỹ thuật hiện đại, từ các công trình xây dựng lớn đến các thiết bị cơ khí chi tiết. Việc hiểu và áp dụng đúng quy tắc này giúp đảm bảo an toàn và hiệu quả trong nhiều lĩnh vực công nghiệp và kỹ thuật.

Để hiểu rõ hơn về quy tắc hợp lực song song ngược chiều, chúng ta cùng xem xét một số ví dụ minh họa sau đây:

1. Ví dụ 1: Hai người kéo một vật theo hai hướng ngược nhau

   Giả sử có hai người đang kéo một chiếc hộp, mỗi người đứng ở một phía đối diện của hộp và kéo về phía mình. Lực kéo của người thứ nhất là \( F_1 = 50 \, \text{N} \), và lực kéo của người thứ hai là \( F_2 = 30 \, \text{N} \). Hai lực này song song và ngược chiều nhau.

   Hợp lực tác dụng lên hộp sẽ được tính như sau:

   \[
   F = |F_1 - F_2| = |50 \, \text{N} - 30 \, \text{N}| = 20 \, \text{N}
   \]

   Hợp lực có độ lớn 20 N và hướng về phía người có lực lớn hơn, tức là về phía người thứ nhất.

2. Ví dụ 2: Tác dụng của hai lực trên một thanh dầm

   Xét một thanh dầm nằm ngang với hai lực song song ngược chiều tác dụng lên nó. Giả sử lực \( F_1 = 100 \, \text{N} \) tác dụng lên đầu bên trái của thanh, và lực \( F_2 = 75 \, \text{N} \) tác dụng lên đầu bên phải.

   Để tìm vị trí của hợp lực trên thanh, ta sử dụng công thức:

   \[
   \frac{d_2}{d_1} = \frac{F_1}{F_2} = \frac{100}{75} = \frac{4}{3}
   \]

   Điều này có nghĩa là hợp lực sẽ nằm gần điểm tác dụng của lực \( F_2 \) hơn, với tỉ lệ khoảng cách giữa hai lực là 4:3.

3. Ví dụ 3: Cầu chịu tải trọng từ hai phía

   Xét một cây cầu chịu tải từ hai phía với các lực tương ứng là \( F_1 = 5000 \, \text{N} \) từ một phía và \( F_2 = 4000 \, \text{N} \) từ phía đối diện. Các lực này song song và ngược chiều nhau.

   Hợp lực tác dụng lên cầu sẽ là:

   \[
   F = |F_1 - F_2| = |5000 \, \text{N} - 4000 \, \text{N}| = 1000 \, \text{N}
   \]

   Hợp lực này sẽ hướng về phía lực lớn hơn, tức là phía của lực \( F_1 \).

Các ví dụ trên minh họa rõ ràng cách quy tắc hợp lực song song ngược chiều được áp dụng trong thực tế, từ các bài toán đơn giản đến những ứng dụng phức tạp trong kỹ thuật và xây dựng.

Khi nghiên cứu về quy tắc hợp lực song song ngược chiều, có một số khái niệm liên quan khác cũng rất quan trọng để hiểu rõ hơn về hiện tượng này và cách nó ứng dụng trong thực tế. Dưới đây là một số khái niệm cơ bản liên quan:

1. Hợp lực:

   Hợp lực là lực tổng hợp được tạo ra từ hai hay nhiều lực tác dụng đồng thời lên một vật. Khi các lực này cùng chiều, hợp lực sẽ là tổng của các lực. Khi ngược chiều, hợp lực sẽ là hiệu của các lực, và hướng của nó theo hướng của lực lớn hơn.

2. Điểm đặt lực:

   Điểm đặt lực là vị trí trên vật thể mà tại đó lực tác động. Vị trí của điểm đặt lực ảnh hưởng đến cách mà lực tác động lên vật thể, và trong trường hợp hai lực song song ngược chiều, nó quyết định vị trí của hợp lực.

3. Momen lực:

   Momen lực là đại lượng đo lường khả năng làm quay của một lực tác dụng lên một vật quanh một điểm hoặc một trục. Momen lực được tính bằng tích của lực và khoảng cách từ điểm đặt lực đến trục quay. Công thức tính momen lực là:

   \[
   M = F \times d
   \]

   Trong đó \( M \) là momen lực, \( F \) là độ lớn của lực, và \( d \) là khoảng cách từ trục quay đến điểm đặt lực.

4. Điều kiện cân bằng của một vật:

   Một vật sẽ ở trạng thái cân bằng khi tổng hợp lực tác dụng lên vật bằng không và tổng momen lực quanh một điểm bất kỳ cũng bằng không. Điều này có nghĩa là các lực tác động phải được cân bằng, và không có xu hướng làm vật di chuyển hoặc quay.

5. Lực đối kháng:

   Lực đối kháng là lực tác động lên vật theo hướng ngược lại với một lực khác, có tác dụng chống lại hoặc cân bằng lực đó. Trong quy tắc hợp lực song song ngược chiều, lực đối kháng đóng vai trò quan trọng trong việc xác định hợp lực và vị trí tác dụng của nó.

Việc hiểu rõ các khái niệm liên quan này giúp làm sáng tỏ thêm về cách mà quy tắc hợp lực song song ngược chiều hoạt động và áp dụng trong các bài toán vật lý cũng như trong thực tiễn.