Công Thức Tổng Hợp Lực: Hướng Dẫn Chi Tiết và Ví Dụ Minh Họa

Công thức tổng hợp lực là một phần kiến thức quan trọng trong môn Vật lý lớp 10, giúp học sinh hiểu và áp dụng để giải các bài toán liên quan đến lực. Tổng hợp lực là việc thay thế các lực tác dụng đồng thời vào một vật bằng một lực có cùng tác dụng. Dưới đây là các nội dung chi tiết về công thức tổng hợp lực.

1. Định nghĩa

Lực là đại lượng vectơ đặc trưng cho tác dụng của vật này lên vật khác, gây ra gia tốc hoặc biến dạng.

Tổng hợp lực là thay thế các lực tác dụng đồng thời vào cùng một vật bằng một lực có tác dụng tương đương, được gọi là hợp lực.

2. Quy tắc hình bình hành

Tổng hợp hai lực đồng quy có thể thực hiện theo quy tắc hình bình hành:

• Nếu hai lực đồng quy làm thành hai cạnh của một hình bình hành, thì đường chéo kẻ từ điểm đồng quy biểu diễn hợp lực của chúng.

3. Công thức tổng hợp lực

Giả sử hai lực \(\vec{F}_1\) và \(\vec{F}_2\) hợp với nhau một góc \(\alpha\). Hợp lực của chúng có độ lớn được tính theo công thức:

\[ F = \sqrt{F_1^2 + F_2^2 + 2F_1F_2\cos{\alpha}} \]

• Nếu \(\alpha = 0^\circ\) (hai lực cùng hướng): \(F = F_1 + F_2\)
• Nếu \(\alpha = 180^\circ\) (hai lực ngược hướng): \(F = |F_1 - F_2|\)
• Nếu \(\alpha = 90^\circ\) (hai lực vuông góc): \(F = \sqrt{F_1^2 + F_2^2}\)

4. Ví dụ áp dụng

Giả sử hai lực đồng quy \(\vec{F}_1\) và \(\vec{F}_2\) có độ lớn lần lượt là 6 N và 8 N, và hợp với nhau một góc vuông (\(90^\circ\)). Hợp lực của chúng được tính như sau:

\[ F = \sqrt{6^2 + 8^2} = \sqrt{36 + 64} = \sqrt{100} = 10 \text{ N} \]

Do đó, hợp lực của hai lực này là 10 N.

5. Ứng dụng

Công thức tổng hợp lực được ứng dụng rộng rãi trong việc giải quyết các bài toán về lực trong cơ học, như tính toán lực tác dụng lên vật thể, phân tích các hệ lực phức tạp, và nhiều bài toán thực tế khác.

6. Bài tập thực hành

Dưới đây là một số bài tập áp dụng công thức tổng hợp lực:

1. Hai lực có độ lớn 5 N và 12 N hợp với nhau một góc \(60^\circ\). Tính độ lớn hợp lực.
2. Một vật chịu tác dụng của hai lực có độ lớn 10 N và 24 N, hợp với nhau một góc \(90^\circ\). Tính hợp lực tác dụng lên vật.
3. Tìm độ lớn của hợp lực khi hai lực có độ lớn bằng nhau và hợp với nhau một góc \(120^\circ\).

Công thức tổng hợp lực là một trong những khái niệm cơ bản và quan trọng trong Vật lý, đặc biệt là trong cơ học. Khi nhiều lực tác dụng đồng thời lên một vật, ta cần thay thế các lực đó bằng một lực duy nhất có tác dụng tương đương, được gọi là hợp lực. Việc xác định hợp lực giúp hiểu rõ hơn về tác động tổng hợp của các lực và cách chúng ảnh hưởng đến chuyển động của vật thể.

Để tổng hợp lực, người ta thường sử dụng quy tắc hình bình hành. Đây là phương pháp hình học giúp tìm hợp lực bằng cách vẽ các lực thành phần như các cạnh của một hình bình hành, và hợp lực chính là đường chéo của hình bình hành đó.

Công thức tổng hợp lực cho hai lực \(\vec{F}_1\) và \(\vec{F}_2\) hợp với nhau một góc \(\alpha\) được tính như sau:

\[ F = \sqrt{F_1^2 + F_2^2 + 2F_1F_2\cos{\alpha}} \]

Nếu hai lực vuông góc (\(\alpha = 90^\circ\)):

\[ F = \sqrt{F_1^2 + F_2^2} \]

Trong trường hợp hai lực cùng phương (\(\alpha = 0^\circ\)):

\[ F = F_1 + F_2 \]

Ngược lại, nếu hai lực ngược hướng (\(\alpha = 180^\circ\)):

\[ F = |F_1 - F_2| \]

Công thức tổng hợp lực không chỉ giúp chúng ta tính toán các lực trong các bài toán cơ học mà còn áp dụng rộng rãi trong thực tế, từ thiết kế công trình xây dựng đến giải quyết các bài toán động lực học phức tạp.

Quy tắc hình bình hành là phương pháp được sử dụng phổ biến trong vật lý để tổng hợp hai lực đồng quy. Theo quy tắc này, nếu hai lực đồng quy \(\overrightarrow{F_1}\) và \(\overrightarrow{F_2}\) được biểu diễn bằng hai cạnh kề của một hình bình hành, thì hợp lực \(\overrightarrow{F}\) của chúng sẽ được biểu diễn bởi đường chéo của hình bình hành xuất phát từ điểm đồng quy.

2.1 Giải thích quy tắc hình bình hành

Giả sử có hai lực \(\overrightarrow{F_1}\) và \(\overrightarrow{F_2}\) tác dụng đồng thời lên một vật tại một điểm. Chúng ta có thể hình dung hai lực này như hai cạnh của một hình bình hành. Đường chéo của hình bình hành, xuất phát từ điểm tác dụng của hai lực, sẽ biểu diễn hợp lực \(\overrightarrow{F}\). Hợp lực này có tác dụng tương đương với việc hai lực \(\overrightarrow{F_1}\) và \(\overrightarrow{F_2}\) tác dụng đồng thời lên vật.

Công thức để tính độ lớn của hợp lực \(\overrightarrow{F}\) được cho bởi:

Trong đó:

• \(F_1\), \(F_2\) là độ lớn của hai lực thành phần.
• \(\varphi\) là góc hợp bởi hai lực \(\overrightarrow{F_1}\) và \(\overrightarrow{F_2}\).

2.2 Các bước thực hiện tổng hợp lực theo quy tắc hình bình hành

1. Xác định các lực thành phần \(\overrightarrow{F_1}\) và \(\overrightarrow{F_2}\) về phương, chiều và độ lớn.
2. Vẽ hai véc-tơ lực \(\overrightarrow{F_1}\) và \(\overrightarrow{F_2}\) xuất phát từ cùng một điểm, tạo thành hai cạnh kề của một hình bình hành.
3. Hoàn thành hình bình hành bằng cách vẽ các cạnh song song với hai lực ban đầu.
4. Vẽ đường chéo của hình bình hành xuất phát từ điểm đồng quy; đường chéo này chính là véc-tơ biểu diễn hợp lực \(\overrightarrow{F}\).
5. Tính toán độ lớn của hợp lực theo công thức trên.

Các trường hợp đặc biệt:

• Nếu hai lực cùng phương (góc giữa chúng là \(0^\circ\)): Hợp lực có độ lớn bằng tổng độ lớn của hai lực \(\overrightarrow{F} = F_1 + F_2\).
• Nếu hai lực vuông góc nhau (\(\varphi = 90^\circ\)): Hợp lực được tính bằng công thức \(\overrightarrow{F} = \sqrt{F_1^2 + F_2^2}\).
• Nếu hai lực ngược chiều nhau (\(\varphi = 180^\circ\)): Hợp lực có độ lớn bằng hiệu độ lớn của hai lực \(\overrightarrow{F} = |F_1 - F_2|\).

Dưới đây là một số ví dụ minh họa và bài tập ứng dụng giúp bạn hiểu rõ hơn về cách tổng hợp lực, đặc biệt là trong các trường hợp thực tế và trong đề thi.

4.1 Ví dụ tổng hợp lực trong bài toán thực tế

Ví dụ 1: Hai lực có độ lớn lần lượt là \( F_1 = 5 \, \text{N} \) và \( F_2 = 7 \, \text{N} \), hợp lực của chúng là bao nhiêu nếu góc giữa hai lực là \( 60^\circ \)?

Giải:

Hợp lực \( F \) của hai lực đồng quy có thể tính bằng công thức:

Thay số vào ta có:

Ví dụ 2: Một vật nằm trên mặt phẳng nghiêng với góc nghiêng \( 30^\circ \). Lực trọng trường tác dụng lên vật là \( 50 \, \text{N} \). Xác định các thành phần của lực này theo phương vuông góc và song song với mặt nghiêng.

Giải:

Trọng lực \( P \) có thể được phân tích thành hai thành phần:

• Thành phần vuông góc với mặt phẳng nghiêng: \( P_1 = P \cdot \cos \alpha = 50 \cdot \cos 30^\circ = 50 \cdot \frac{\sqrt{3}}{2} \approx 43.3 \, \text{N} \)
• Thành phần song song với mặt phẳng nghiêng: \( P_2 = P \cdot \sin \alpha = 50 \cdot \sin 30^\circ = 50 \cdot 0.5 = 25 \, \text{N} \)

4.2 Bài tập tự luyện tổng hợp lực

Dưới đây là một số bài tập tự luyện để bạn có thể thực hành về tổng hợp lực:

1. Tính hợp lực của hai lực đồng quy \( F_1 = 10 \, \text{N} \) và \( F_2 = 15 \, \text{N} \) khi góc giữa chúng là \( 90^\circ \).
2. Ba lực \( F_1 = 20 \, \text{N} \), \( F_2 = 20 \, \text{N} \), và \( F_3 = 20 \, \text{N} \) đồng quy tạo với nhau các góc \( 120^\circ \). Tính hợp lực của chúng.
3. Một vật nặng 5kg được treo trên một sợi dây với một lực căng là \( T = 49 \, \text{N} \). Xác định các thành phần lực khi góc giữa sợi dây và phương ngang là \( 30^\circ \).
4. Tính lực ma sát khi một vật nặng 2kg trượt trên mặt phẳng nghiêng với góc nghiêng \( 30^\circ \), biết hệ số ma sát là \( 0.3 \).
5. Một vật chịu tác dụng của ba lực: \( F_1 = 5 \, \text{N} \) hướng về phía đông, \( F_2 = 5 \, \text{N} \) hướng về phía tây, và \( F_3 = 10 \, \text{N} \) hướng về phía bắc. Xác định điều kiện cân bằng của vật.

Trong vật lý, phân tích lực là một quá trình quan trọng để hiểu rõ hơn về cách các lực tác động lên vật thể. Khi một vật chịu tác động bởi nhiều lực, chúng ta có thể phân tích các lực này thành các thành phần đơn giản hơn theo các phương khác nhau. Điều này giúp trong việc giải quyết các bài toán liên quan đến cân bằng và chuyển động.

5.1 Phân tích lực thành các thành phần trên các trục tọa độ

Để phân tích lực, chúng ta thường tiến hành theo các bước sau:

1. Xác định hệ tọa độ: Thiết lập một hệ trục tọa độ phù hợp với vấn đề. Thường thì trục Ox sẽ theo hướng nằm ngang và Oy theo hướng thẳng đứng.
2. Vẽ lực cần phân tích: Lực cần phân tích được biểu diễn dưới dạng một vectơ trong hệ tọa độ.
3. Phân tích lực: Sử dụng các công thức lượng giác để chia lực thành các thành phần theo trục Ox và Oy. Giả sử lực \( \mathbf{F} \) tạo góc \( \alpha \) so với trục Ox, ta có các thành phần: \[ F_x = F \cos(\alpha) \] \[ F_y = F \sin(\alpha) \] Trong đó, \( F_x \) và \( F_y \) lần lượt là các thành phần của lực theo trục Ox và Oy.

Việc phân tích lực giúp chúng ta hiểu rõ hơn về sự tác động của các lực trong các bài toán vật lý và ứng dụng thực tế như thiết kế công trình hoặc tính toán cơ học.

5.2 Phân loại các lực trong vật lý: lực đàn hồi, lực ma sát, lực hấp dẫn

Trong vật lý, các lực cơ bản thường được phân loại thành:

• Lực đàn hồi: Xuất hiện khi một vật bị biến dạng như kéo dài hoặc nén lại. Lực này có xu hướng đưa vật trở lại trạng thái ban đầu.
• Lực ma sát: Xuất hiện khi hai bề mặt tiếp xúc chuyển động tương đối so với nhau. Lực ma sát có thể ngăn cản chuyển động hoặc làm chậm nó lại.
• Lực hấp dẫn: Là lực hút giữa hai vật có khối lượng, ví dụ như lực hút của Trái Đất lên các vật trên bề mặt.

Việc hiểu rõ các loại lực cơ bản này là nền tảng quan trọng trong nhiều lĩnh vực vật lý và kỹ thuật, từ cơ học cổ điển đến cơ học lượng tử.

Trong các hệ vật lý phức tạp, việc tổng hợp lực trở nên khó khăn hơn do sự tương tác giữa nhiều lực đồng thời tác động lên vật thể. Việc phân tích và tổng hợp các lực này đòi hỏi phải áp dụng các phương pháp phức tạp hơn so với trường hợp hai lực đơn giản.

6.1 Tổng hợp lực trong hệ nhiều lực đồng quy

Khi nhiều lực đồng quy tác dụng lên một điểm, ta cần tìm hợp lực của chúng. Để thực hiện điều này, ta có thể áp dụng quy tắc hình bình hành hoặc phương pháp giải tích. Với quy tắc hình bình hành, mỗi cặp lực được tổng hợp để tạo ra một lực mới, sau đó lực mới này lại tiếp tục được tổng hợp với lực tiếp theo. Quá trình này tiếp tục cho đến khi tất cả các lực được tổng hợp thành một hợp lực duy nhất.

Công thức tính hợp lực cho hệ nhiều lực đồng quy được thể hiện như sau:

• Nếu các lực \( \vec{F}_1, \vec{F}_2, \ldots, \vec{F}_n \) có các thành phần theo trục \( x \) và \( y \), hợp lực \( \vec{R} \) có thành phần theo các trục là: \[ R_x = \sum_{i=1}^{n} F_{ix}, \quad R_y = \sum_{i=1}^{n} F_{iy} \]
• Độ lớn của hợp lực được tính bằng: \[ R = \sqrt{R_x^2 + R_y^2} \]
• Góc \( \theta \) hợp bởi hợp lực \( \vec{R} \) với trục \( x \) là: \[ \theta = \tan^{-1}\left(\frac{R_y}{R_x}\right) \]

6.2 Ứng dụng tổng hợp lực trong cơ học kỹ thuật và xây dựng

Trong các ứng dụng thực tế như xây dựng và cơ học kỹ thuật, việc tổng hợp lực rất quan trọng để đảm bảo tính ổn định và an toàn của các cấu trúc. Ví dụ, khi tính toán tải trọng tác dụng lên các thanh trong một kết cấu cầu, ta cần xác định tổng hợp lực để biết được lực tác dụng lên mỗi thanh.

Một ví dụ phổ biến là tính toán lực tác dụng lên một thanh chịu uốn xiên, nơi các mô-men uốn quanh hai trục chính được tổng hợp thành một mô-men uốn tổng hợp. Quá trình này giúp xác định ứng suất tác dụng lên các mặt cắt của thanh, từ đó đánh giá được độ bền và khả năng chịu tải của cấu trúc.

Phương pháp phân tích này không chỉ quan trọng trong các bài toán lý thuyết mà còn trong việc thiết kế các công trình thực tế, đảm bảo rằng mọi lực tác động được tính toán chính xác để tránh rủi ro.

Trong vật lý, ngoài công thức tổng hợp lực, còn có nhiều công thức khác liên quan đến lực, công, và năng lượng. Các công thức này đóng vai trò quan trọng trong việc giải quyết các bài toán phức tạp và phân tích các hiện tượng vật lý khác nhau. Dưới đây là một số công thức liên quan và bổ sung:

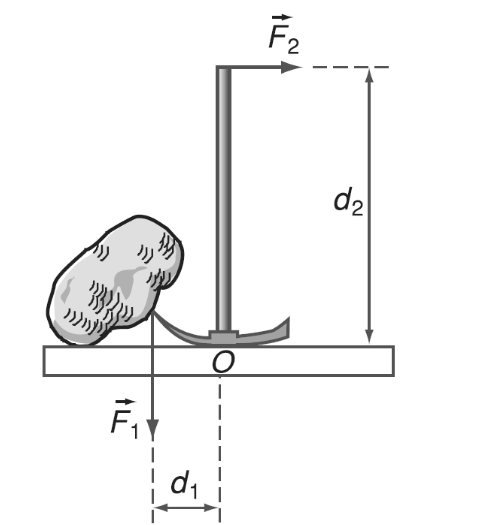
7.1 Công thức tính moment lực

Moment lực là đại lượng đặc trưng cho khả năng gây quay của lực quanh một điểm hoặc một trục. Công thức tính moment lực được cho bởi:

Trong đó:

• \(M\): Moment lực (Nm).
• \(F\): Độ lớn của lực tác dụng (N).
• \(d\): Khoảng cách từ điểm đặt lực đến trục quay (m).
• \(\theta\): Góc giữa hướng của lực và đoạn thẳng nối điểm đặt lực với trục quay (độ).

7.2 Công thức tính công của lực

Công của lực là đại lượng đo lường năng lượng mà lực tác dụng làm biến đổi trạng thái chuyển động của vật. Công của lực được tính bằng công thức:

Trong đó:

• \(A\): Công của lực (Joule).
• \(F\): Độ lớn của lực tác dụng (N).
• \(s\): Quãng đường mà vật di chuyển (m).
• \(\alpha\): Góc giữa hướng của lực và hướng di chuyển của vật (độ).

7.3 Công suất và năng lượng liên quan đến lực

Công suất là đại lượng đặc trưng cho tốc độ thực hiện công của lực, và nó được tính bằng công thức:

Trong đó:

• \(P\): Công suất (Watt).
• \(A\): Công thực hiện (Joule).
• \(t\): Thời gian thực hiện công (giây).

Ngoài ra, công suất cũng có thể được biểu diễn dưới dạng:

Trong đó \(v\) là vận tốc của vật (m/s) theo hướng của lực.

Những công thức này không chỉ bổ sung cho việc tính toán trong các hệ thống cơ học mà còn có nhiều ứng dụng thực tế trong kỹ thuật, xây dựng và nhiều lĩnh vực khác.

Để nắm vững các khái niệm và công thức về tổng hợp lực, dưới đây là một số tài liệu học tập và tham khảo hữu ích cho bạn:

• Sách giáo khoa và sách tham khảo:
  • Vật lý lớp 10 - Đây là nguồn tài liệu cơ bản giúp bạn hiểu rõ về các khái niệm và quy tắc liên quan đến tổng hợp lực, bao gồm quy tắc hình bình hành và các trường hợp đặc biệt.
  • Cơ học lý thuyết - Một tài liệu chuyên sâu, phù hợp cho những ai muốn tìm hiểu kỹ lưỡng về các nguyên lý cơ học liên quan đến tổng hợp lực.
• Bài giảng video và các nguồn học liệu trực tuyến:
  • - Cung cấp bài giảng chi tiết về tổng hợp lực và phân tích lực, bao gồm cả lý thuyết và bài tập ứng dụng.
  • - Website với nhiều bài tập và tài liệu thực hành, giúp củng cố kiến thức và kỹ năng qua các ví dụ thực tế.
• Tài liệu tham khảo khác:
  • - Hướng dẫn cụ thể các bước thực hiện thí nghiệm và cách tính toán lực tổng hợp trong các hệ lực phức tạp.
  • - Tài liệu lý thuyết và bài tập dành cho học sinh lớp 10, với các dạng bài tập từ cơ bản đến nâng cao.