Tổng hợp lực: Khái niệm, phương pháp và ứng dụng trong đời sống

Tổng hợp lực là một trong những khái niệm cơ bản trong vật lý, đặc biệt trong phần động lực học. Nó liên quan đến việc kết hợp hai hay nhiều lực tác dụng lên một vật thể để xác định hợp lực - lực tổng cộng tác dụng lên vật đó.

Khái niệm và phương pháp tổng hợp lực

Khi nhiều lực cùng tác dụng lên một vật, hợp lực là lực duy nhất có thể thay thế các lực này mà vẫn tạo ra cùng một tác động. Hợp lực được tìm bằng phương pháp hình học hoặc phương pháp đại số.

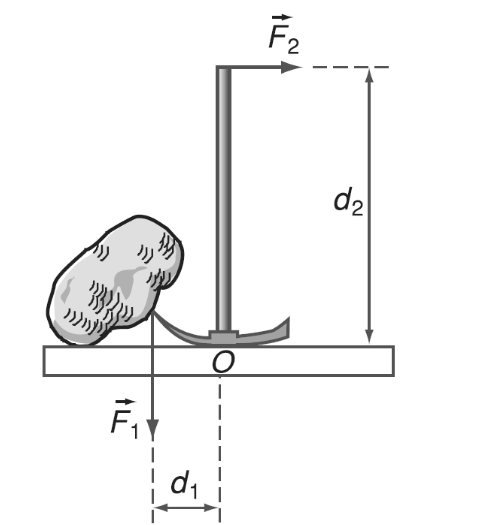
• Phương pháp hình học: Thường sử dụng quy tắc hình bình hành. Nếu hai lực \(\vec{F}_1\) và \(\vec{F}_2\) đồng thời tác dụng lên một điểm, hợp lực \(\vec{F}\) được biểu diễn bởi đường chéo của hình bình hành tạo bởi \(\vec{F}_1\) và \(\vec{F}_2\).
• Phương pháp đại số: Trong hệ tọa độ, các lực được phân tích theo các trục tọa độ. Hợp lực sẽ là tổng các lực thành phần theo từng trục.

Công thức tổng hợp lực

Giả sử có hai lực \(\vec{F}_1\) và \(\vec{F}_2\) hợp thành một góc \(\theta\), hợp lực \(\vec{F}\) có độ lớn được tính theo công thức:

\[
F = \sqrt{F_1^2 + F_2^2 + 2F_1F_2\cos\theta}
\]

Trong trường hợp hai lực vuông góc với nhau (\(\theta = 90^\circ\)):

\[
F = \sqrt{F_1^2 + F_2^2}
\]

Ứng dụng của tổng hợp lực

Tổng hợp lực có nhiều ứng dụng trong đời sống và kỹ thuật, ví dụ:

• Xây dựng: Tính toán lực tác dụng lên các công trình như cầu, nhà cao tầng.
• Cơ khí: Phân tích lực tác dụng lên các bộ phận của máy móc.
• Giao thông vận tải: Tính toán lực kéo, lực cản trong thiết kế xe cộ.

Bài toán tổng hợp lực

Ví dụ, xét bài toán sau:

Một vật chịu tác dụng của hai lực \(\vec{F}_1\) và \(\vec{F}_2\) với độ lớn lần lượt là 30N và 40N, hợp với nhau một góc 60°. Hãy tính hợp lực tác dụng lên vật.

Lời giải:

Sử dụng công thức tổng hợp lực:

\[
F = \sqrt{30^2 + 40^2 + 2 \cdot 30 \cdot 40 \cdot \cos 60^\circ}
\]

Kết quả:

\[
F = \sqrt{900 + 1600 + 2400} = \sqrt{4900} = 70N
\]

Vậy hợp lực tác dụng lên vật là 70N.

Kết luận

Tổng hợp lực là một kỹ thuật quan trọng trong vật lý, giúp giải quyết các bài toán liên quan đến nhiều lực tác dụng đồng thời lên một vật. Hiểu rõ và vận dụng đúng phương pháp tổng hợp lực sẽ giúp chúng ta giải quyết được nhiều vấn đề trong thực tế.

Tổng hợp lực là quá trình tìm ra một lực duy nhất có thể thay thế tác dụng của nhiều lực cùng lúc lên một vật, sao cho lực này tạo ra cùng một tác dụng như các lực ban đầu. Lực này được gọi là hợp lực.

Khi các lực tác dụng lên một vật không cùng phương, ta cần tổng hợp chúng để tìm ra lực tổng cộng. Để thực hiện điều này, chúng ta sử dụng hai phương pháp chính: phương pháp hình học và phương pháp đại số.

• Phương pháp hình học: Dùng quy tắc hình bình hành để xác định hợp lực. Nếu hai lực \(\vec{F}_1\) và \(\vec{F}_2\) hợp với nhau một góc \(\theta\), thì hợp lực \(\vec{F}\) được biểu diễn bởi đường chéo của hình bình hành được tạo bởi hai lực này.
• Phương pháp đại số: Phân tích các lực thành các thành phần theo các trục tọa độ và tổng hợp từng thành phần theo từng trục. Hợp lực sẽ là tổng đại số của các thành phần lực này.

Công thức tổng hợp lực khi hai lực \(\vec{F}_1\) và \(\vec{F}_2\) hợp với nhau một góc \(\theta\) được tính như sau:

\[
F = \sqrt{F_1^2 + F_2^2 + 2F_1F_2\cos\theta}
\]

Nếu hai lực vuông góc với nhau (\(\theta = 90^\circ\)), công thức được đơn giản hóa:

\[
F = \sqrt{F_1^2 + F_2^2}
\]

Trường hợp đặc biệt, nếu hai lực có cùng phương và cùng chiều, hợp lực sẽ là tổng của hai lực:

\[
F = F_1 + F_2
\]

Ngược lại, nếu hai lực cùng phương nhưng ngược chiều, hợp lực sẽ là hiệu của hai lực:

\[
F = |F_1 - F_2|
\]

Tổng hợp lực là bước đầu tiên trong việc phân tích các bài toán động lực học và có vai trò quan trọng trong nhiều ứng dụng thực tế.

Trong vật lý, có hai phương pháp chính để tổng hợp lực: phương pháp hình học và phương pháp đại số. Mỗi phương pháp có ưu điểm và cách áp dụng riêng, tùy thuộc vào tình huống cụ thể.

• Phương pháp hình học: Đây là phương pháp phổ biến nhất để tổng hợp hai lực không đồng phương. Phương pháp này sử dụng quy tắc hình bình hành.

1. Xác định độ lớn và hướng của từng lực.
2. Vẽ các vector lực \(\vec{F}_1\) và \(\vec{F}_2\) từ một điểm chung.
3. Vẽ đường chéo của hình bình hành mà hai cạnh là hai vector lực. Đường chéo này chính là hợp lực \(\vec{F}\).

Công thức hình học cho hợp lực \(\vec{F}\) trong trường hợp này là:

\[
F = \sqrt{F_1^2 + F_2^2 + 2F_1F_2\cos\theta}
\]

Trong đó, \(\theta\) là góc giữa hai lực.

• Phương pháp đại số: Phương pháp này được sử dụng khi các lực có phương thẳng hàng hoặc vuông góc với nhau. Để tổng hợp lực bằng phương pháp đại số, các bước sau được thực hiện:

1. Phân tích mỗi lực thành các thành phần trên các trục tọa độ (thường là trục \(x\) và \(y\)).
2. Cộng các thành phần lực theo từng trục để tìm hợp lực trên trục \(x\) và trục \(y\).
3. Tính hợp lực tổng hợp bằng cách sử dụng định lý Pythagore nếu hai lực vuông góc hoặc công thức tổng hợp lực nếu không vuông góc.

Ví dụ, với hai lực vuông góc nhau:

\[
F = \sqrt{F_x^2 + F_y^2}
\]

Trong đó \(F_x\) và \(F_y\) là các thành phần lực trên trục \(x\) và \(y\).

Cả hai phương pháp trên đều có thể được sử dụng để giải quyết các bài toán thực tế trong kỹ thuật, cơ khí và các lĩnh vực liên quan.

Tổng hợp lực là một khái niệm quan trọng trong vật lý, đặc biệt khi phân tích các lực tác dụng lên một vật thể. Để tính hợp lực, ta cần áp dụng các công thức phù hợp với từng trường hợp cụ thể.

Công thức tổng hợp lực

• Trường hợp 1: Khi hai lực \(\vec{F}_1\) và \(\vec{F}_2\) hợp với nhau một góc \(\theta\), công thức tổng hợp lực được sử dụng là:

\[
F = \sqrt{F_1^2 + F_2^2 + 2F_1F_2\cos\theta}
\]

• Trong đó:
• \(F_1\), \(F_2\) là độ lớn của hai lực tác dụng.
• \(\theta\) là góc giữa hai lực.
• Trường hợp 2: Khi hai lực vuông góc với nhau (\(\theta = 90^\circ\)), công thức sẽ đơn giản hơn:

\[
F = \sqrt{F_1^2 + F_2^2}
\]

• Trường hợp 3: Khi hai lực cùng phương và cùng chiều, hợp lực là tổng đại số của hai lực:

\[
F = F_1 + F_2
\]

• Trường hợp 4: Khi hai lực cùng phương nhưng ngược chiều, hợp lực là hiệu đại số của hai lực:

\[
F = |F_1 - F_2|
\]

Bài toán tổng hợp lực

Để hiểu rõ hơn về việc áp dụng các công thức tổng hợp lực, chúng ta xét một bài toán cụ thể:

Bài toán: Một vật chịu tác dụng của hai lực \(\vec{F}_1 = 30N\) và \(\vec{F}_2 = 40N\), hợp với nhau một góc \(60^\circ\). Hãy tính hợp lực tác dụng lên vật.

1. Áp dụng công thức tổng hợp lực cho hai lực không vuông góc:

\[
F = \sqrt{30^2 + 40^2 + 2 \cdot 30 \cdot 40 \cdot \cos 60^\circ}
\]

1. Tính toán:

\[
F = \sqrt{900 + 1600 + 2400 \cdot 0.5} = \sqrt{4900} = 70N
\]

Vậy hợp lực tác dụng lên vật là \(70N\).

Bài toán trên minh họa cách áp dụng công thức tổng hợp lực để giải quyết các vấn đề liên quan đến lực trong thực tế.

Tổng hợp lực là một khái niệm cơ bản trong vật lý, nhưng lại có rất nhiều ứng dụng thực tiễn trong đời sống và kỹ thuật. Dưới đây là một số ví dụ điển hình về cách tổng hợp lực được áp dụng trong các lĩnh vực khác nhau:

• Trong xây dựng và kiến trúc: Tổng hợp lực giúp các kỹ sư xây dựng tính toán chính xác lực tác dụng lên các cấu trúc như cầu, tòa nhà hay các công trình khác. Nhờ đó, họ có thể thiết kế các công trình chịu được tải trọng và đảm bảo an toàn.
• Trong kỹ thuật và cơ khí: Việc tổng hợp lực là rất quan trọng trong việc thiết kế và vận hành các máy móc, thiết bị. Chẳng hạn, trong thiết kế ô tô, kỹ sư phải tính toán lực tổng hợp từ động cơ, phanh và các yếu tố khác để đảm bảo hiệu suất và an toàn của xe.
• Trong giao thông và vận tải: Tổng hợp lực giúp tính toán lực cản gió, lực ma sát và lực đẩy của động cơ để tối ưu hóa hoạt động của các phương tiện giao thông. Điều này đặc biệt quan trọng đối với việc thiết kế máy bay, tàu thuyền và xe cộ.
• Trong thể thao: Vận động viên và huấn luyện viên sử dụng kiến thức về tổng hợp lực để tối ưu hóa kỹ thuật và hiệu suất trong các môn thể thao như điền kinh, bơi lội hay bóng đá. Việc hiểu rõ cách các lực tác dụng lên cơ thể giúp cải thiện thành tích và giảm nguy cơ chấn thương.
• Trong đời sống hàng ngày: Từ việc đẩy xe hàng trong siêu thị đến việc kéo vali du lịch, mọi người đều sử dụng tổng hợp lực một cách tự nhiên mà không nhận ra. Sự phối hợp của các lực giúp chúng ta thực hiện các hoạt động một cách hiệu quả và dễ dàng hơn.

Nhờ vào tổng hợp lực, chúng ta có thể hiểu rõ hơn về các hiện tượng xung quanh và ứng dụng chúng để cải thiện cuộc sống hàng ngày cũng như trong các lĩnh vực kỹ thuật phức tạp.

Để học tập và hiểu rõ hơn về tổng hợp lực, có nhiều công cụ và tài nguyên hỗ trợ từ sách vở, phần mềm đến các nền tảng trực tuyến. Dưới đây là một số công cụ hữu ích mà học sinh và sinh viên có thể sử dụng để nâng cao kiến thức của mình.

• Sách giáo khoa và tài liệu tham khảo: Đây là nguồn kiến thức nền tảng về tổng hợp lực, với các ví dụ minh họa chi tiết và bài tập thực hành. Các cuốn sách này thường được sử dụng trong chương trình học chính quy.
• Phần mềm mô phỏng: Các phần mềm như PhET Interactive Simulations cung cấp các mô phỏng trực quan về cách tổng hợp lực trong các tình huống khác nhau. Học sinh có thể thực hành và quan sát trực tiếp kết quả từ các lực tác dụng lên một vật.
• Ứng dụng di động: Hiện nay, có nhiều ứng dụng học tập trên điện thoại di động giúp học sinh làm quen với khái niệm tổng hợp lực thông qua các bài kiểm tra nhanh và trò chơi tương tác.
• Nền tảng học tập trực tuyến: Các trang web như Khan Academy, Coursera và Udemy cung cấp các khóa học chuyên sâu về vật lý, trong đó có phần học về tổng hợp lực. Các khóa học này thường kèm theo video giảng dạy, bài tập và diễn đàn thảo luận.
• Video giảng dạy trên YouTube: Nhiều kênh giáo dục trên YouTube cung cấp các bài giảng miễn phí về tổng hợp lực. Những video này thường giải thích lý thuyết và hướng dẫn giải các bài tập từ cơ bản đến nâng cao.
• Công cụ trực tuyến: Các công cụ tính toán trực tuyến, như máy tính vector, giúp học sinh giải quyết các bài toán tổng hợp lực một cách nhanh chóng và chính xác.

Việc sử dụng các công cụ này không chỉ giúp học sinh nắm vững kiến thức mà còn phát triển kỹ năng thực hành và giải quyết vấn đề một cách hiệu quả.