Hợp Lực Tác Dụng Lên Vật Dao Động Điều Hòa: Hiểu Rõ Từ A Đến Z

Trong vật lý học, hợp lực tác dụng lên vật dao động điều hòa là một khái niệm quan trọng, thường được sử dụng để mô tả sự tương tác giữa các lực khác nhau khi một vật thực hiện dao động điều hòa. Bài viết này sẽ cung cấp một tổng quan chi tiết về các yếu tố chính của hợp lực trong dao động điều hòa.

Tổng Quan Về Dao Động Điều Hòa

Dao động điều hòa là một loại dao động mà trong đó lực tác dụng lên vật luôn hướng về vị trí cân bằng và có độ lớn tỉ lệ thuận với độ lệch của vật so với vị trí cân bằng. Công thức cơ bản cho dao động điều hòa thường được biểu diễn bằng:

\[
F = -kx
\]

trong đó:

• \(F\) là lực kéo về hay hợp lực tác dụng lên vật
• \(k\) là hằng số đàn hồi của hệ
• \(x\) là độ lệch của vật khỏi vị trí cân bằng

Đồ Thị Lực Trong Dao Động Điều Hòa

Đồ thị lực trong dao động điều hòa biểu diễn mối quan hệ giữa lực tác dụng và li độ của vật. Đồ thị này thường là một đường thẳng đi qua gốc tọa độ, với độ dốc phụ thuộc vào hằng số \(k\). Đồ thị có dạng:

\[
F(x) = -kx
\]

Điều này có nghĩa là khi vật ở vị trí cân bằng (tức là \(x = 0\)), lực bằng không; khi vật ở vị trí biên, lực đạt giá trị cực đại.

Ứng Dụng Và Bài Tập Liên Quan

Trong các bài tập liên quan đến dao động điều hòa, hợp lực tác dụng lên vật là một yếu tố then chốt để tính toán các đại lượng như vận tốc, gia tốc và năng lượng của hệ dao động. Một số bài toán phổ biến bao gồm:

1. Tính thời điểm và vị trí mà lực đạt giá trị cực đại.
2. Xác định thời gian mà vật mất để di chuyển giữa hai vị trí nhất định.
3. Tính toán các đại lượng liên quan đến năng lượng của hệ, chẳng hạn như động năng và thế năng.

Tóm Tắt

Hợp lực tác dụng lên vật dao động điều hòa là một chủ đề cốt lõi trong vật lý học, liên quan chặt chẽ đến các khái niệm về lực, năng lượng và dao động. Việc hiểu rõ về hợp lực này không chỉ giúp giải quyết các bài toán vật lý mà còn ứng dụng rộng rãi trong nhiều lĩnh vực khác nhau.

Hy vọng thông tin này sẽ giúp bạn nắm bắt được các khía cạnh cơ bản của hợp lực trong dao động điều hòa.

Hợp lực trong dao động điều hòa là lực tổng hợp từ các lực khác nhau tác dụng lên vật khi vật thực hiện dao động. Trong trường hợp dao động điều hòa, hợp lực này thường là kết quả của lực đàn hồi và các lực khác như trọng lực hoặc lực ma sát.

Khi một vật dao động điều hòa, lực tác dụng lên vật có thể được biểu diễn bằng công thức:

\[
\vec{F} = -k\vec{x}
\]

Trong đó:

• \(\vec{F}\) là hợp lực tác dụng lên vật
• \(k\) là hằng số lực đàn hồi (còn gọi là độ cứng của lò xo)
• \(\vec{x}\) là độ lệch của vật khỏi vị trí cân bằng

Đặc điểm quan trọng của hợp lực trong dao động điều hòa là luôn hướng về vị trí cân bằng của vật và có độ lớn tỉ lệ thuận với độ lệch của vật. Do đó, hợp lực này có vai trò như một lực kéo về, giúp vật quay lại vị trí cân bằng mỗi khi nó bị lệch khỏi vị trí đó.

Trong quá trình dao động, hợp lực sẽ đạt giá trị cực đại khi vật ở vị trí biên, nơi mà độ lệch khỏi vị trí cân bằng là lớn nhất. Ngược lại, tại vị trí cân bằng, hợp lực bằng 0, do vật không còn bị lực nào kéo về.

Hợp lực trong dao động điều hòa đóng vai trò quan trọng trong việc xác định các đặc tính của dao động như chu kỳ, tần số và biên độ dao động.

Các bài toán liên quan đến hợp lực trong dao động điều hòa thường được phân loại dựa trên mục tiêu tính toán và đặc tính của dao động. Dưới đây là một số dạng bài toán phổ biến:

2.1. Bài Toán Tính Hợp Lực Tại Vị Trí Biên Và Vị Trí Cân Bằng

Trong dao động điều hòa, hợp lực đạt giá trị cực đại tại vị trí biên và bằng 0 tại vị trí cân bằng. Công thức tính hợp lực tại vị trí bất kỳ có thể được biểu diễn dưới dạng:

\[
F = -kx
\]

Trong đó \(x\) là li độ của vật. Tại vị trí biên, \(x = \pm A\), do đó hợp lực cực đại là:

\[
F_{max} = kA
\]

Ví dụ, bài toán yêu cầu tính hợp lực khi vật đang ở vị trí cách vị trí cân bằng một đoạn nhất định có thể được giải bằng cách áp dụng công thức trên.

2.2. Bài Toán Về Thời Gian Vật Di Chuyển Giữa Hai Vị Trí

Dạng bài toán này tập trung vào việc tính thời gian vật cần để di chuyển giữa hai vị trí xác định. Để giải quyết, ta cần xác định li độ và vận tốc của vật tại các vị trí đó, sau đó sử dụng công thức liên quan đến chu kỳ dao động:

\[
T = 2\pi \sqrt{\frac{m}{k}}
\]

Ví dụ, thời gian di chuyển từ vị trí cân bằng đến vị trí có li độ \(x_1\) có thể được tính thông qua phân tích pha của dao động.

2.3. Bài Toán Tính Vận Tốc Và Gia Tốc Của Vật

Bài toán này thường yêu cầu tính vận tốc và gia tốc của vật tại các thời điểm hoặc vị trí cụ thể trong quá trình dao động. Vận tốc \(v\) và gia tốc \(a\) có thể được xác định bằng các công thức sau:

• Vận tốc: \[v = \pm \sqrt{k/m (A^2 - x^2)}\]
• Gia tốc: \[a = -\frac{k}{m}x\]

Các bài toán này thường đi kèm với việc xác định giá trị cụ thể tại các vị trí biên hoặc khi vật đi qua vị trí cân bằng.

2.4. Bài Toán Về Năng Lượng Của Vật Dao Động

Dạng bài toán này liên quan đến việc tính toán năng lượng toàn phần, thế năng, và động năng của vật trong quá trình dao động. Tổng năng lượng của hệ dao động điều hòa được bảo toàn và có thể tính bằng:

\[
E = \frac{1}{2}kA^2
\]

Trong đó, thế năng \(U\) và động năng \(K\) tại một vị trí cụ thể được tính như sau:

• Thế năng: \[U = \frac{1}{2}kx^2\]
• Động năng: \[K = \frac{1}{2}mv^2\]

Bài toán thường yêu cầu xác định sự phân bố năng lượng giữa thế năng và động năng tại các vị trí khác nhau của dao động.

Đồ thị liên quan đến hợp lực trong dao động điều hòa là một công cụ quan trọng giúp hiểu rõ sự biến đổi của lực theo thời gian và li độ. Các đồ thị này thường được sử dụng để phân tích và mô tả chi tiết sự thay đổi của lực kéo về trong suốt quá trình dao động.

3.1. Đồ Thị Lực Kéo Về Theo Li Độ

Đồ thị biểu diễn mối quan hệ giữa hợp lực \(F\) và li độ \(x\) của vật dao động điều hòa. Trong dao động điều hòa, mối quan hệ giữa lực và li độ được biểu diễn qua phương trình:

\[
F = -kx
\]

Đồ thị của hàm số này là một đường thẳng đi qua gốc tọa độ với độ dốc âm. Điều này cho thấy lực kéo về luôn tỉ lệ thuận với li độ và luôn hướng về vị trí cân bằng.

3.2. Đồ Thị Lực Theo Thời Gian

Đồ thị này mô tả sự biến thiên của lực theo thời gian trong quá trình dao động. Nếu lực được biểu diễn bằng phương trình:

\[
F(t) = -kA\cos(\omega t + \phi)
\]

thì đồ thị của \(F(t)\) sẽ là một đường hình sin, dao động quanh giá trị 0. Chu kỳ của đồ thị lực tương ứng với chu kỳ dao động của vật, cho thấy sự thay đổi tuần hoàn của hợp lực theo thời gian.

3.3. Đồ Thị So Sánh Giữa Lực, Vận Tốc Và Gia Tốc

Để phân tích chi tiết hơn, có thể vẽ đồ thị so sánh giữa lực, vận tốc và gia tốc theo thời gian. Các đồ thị này đều là các đường hình sin với cùng chu kỳ nhưng khác pha:

• Lực \(F\) và gia tốc \(a\) có cùng pha, cả hai đều có cực đại khi vật ở vị trí biên.
• Vận tốc \(v\) lệch pha với lực và gia tốc một góc \(\pi/2\), đạt giá trị cực đại khi vật đi qua vị trí cân bằng.

Việc so sánh các đồ thị này giúp ta hiểu rõ hơn mối quan hệ giữa các đại lượng vật lý quan trọng trong dao động điều hòa.

Hợp lực trong dao động điều hòa có rất nhiều ứng dụng thực tế trong nhiều lĩnh vực khác nhau của đời sống và công nghệ. Dưới đây là một số ứng dụng tiêu biểu:

4.1. Hệ Thống Treo Ô Tô

Hệ thống treo của ô tô sử dụng nguyên lý dao động điều hòa để giảm chấn và tăng độ êm ái khi di chuyển. Lực kéo về trong lò xo và giảm chấn giúp hạn chế những dao động do mặt đường gồ ghề, từ đó bảo vệ người ngồi trên xe và các bộ phận khác của xe khỏi các tác động xấu.

4.2. Con Lắc Đồng Hồ

Con lắc trong đồng hồ cơ là một ví dụ kinh điển của dao động điều hòa. Hợp lực kéo về trong con lắc đảm bảo cho chuyển động của nó diễn ra đều đặn, tạo ra một nhịp đập chính xác để đo thời gian. Cơ chế này đã được sử dụng trong hàng thế kỷ để tạo ra các loại đồng hồ cơ có độ chính xác cao.

4.3. Các Bộ Phận Của Máy Móc Công Nghiệp

Nhiều bộ phận trong máy móc công nghiệp, như các lò xo trong hệ thống giảm chấn hoặc các cơ cấu dao động khác, đều sử dụng hợp lực trong dao động điều hòa để duy trì độ ổn định và hiệu suất hoạt động. Các cơ cấu này giúp giảm thiểu tác động của dao động không mong muốn, đảm bảo máy móc hoạt động trơn tru và an toàn.

4.4. Thiết Bị Y Tế

Trong y tế, nguyên lý dao động điều hòa được ứng dụng trong nhiều thiết bị như máy đo nhịp tim, máy đo huyết áp, và các thiết bị phân tích rung động khác. Hợp lực giúp các thiết bị này phát hiện và phân tích dao động sinh học, cung cấp thông tin quan trọng về tình trạng sức khỏe của bệnh nhân.

4.5. Kỹ Thuật Xây Dựng

Trong kỹ thuật xây dựng, dao động điều hòa được nghiên cứu kỹ lưỡng để thiết kế các tòa nhà có khả năng chống chịu tốt trước động đất và các lực tác động khác. Các kỹ sư sử dụng nguyên lý hợp lực để tính toán và thiết kế các hệ thống giảm chấn và hấp thụ năng lượng trong các tòa nhà cao tầng.

Trong quá trình giải các bài tập về hợp lực trong dao động điều hòa, việc nắm vững các công thức và mẹo giải nhanh là rất quan trọng. Dưới đây là các công thức cơ bản và một số mẹo hữu ích giúp bạn dễ dàng tiếp cận và giải quyết bài toán.

5.1. Công Thức Tổng Hợp

• Lực kéo về: \[ F = -kx \] - Lực kéo về luôn tỉ lệ thuận với li độ và hướng về vị trí cân bằng.
• Li độ theo thời gian: \[ x(t) = A\cos(\omega t + \phi) \] - Công thức xác định vị trí của vật tại thời điểm t bất kỳ.
• Vận tốc: \[ v(t) = -A\omega\sin(\omega t + \phi) \] - Vận tốc có giá trị cực đại khi vật qua vị trí cân bằng.
• Gia tốc: \[ a(t) = -A\omega^2\cos(\omega t + \phi) \] - Gia tốc tỉ lệ thuận với li độ và luôn ngược hướng với li độ.
• Chu kỳ dao động: \[ T = 2\pi\sqrt{\frac{m}{k}} \] - Chu kỳ của dao động phụ thuộc vào khối lượng và độ cứng của lò xo.
• Thế năng: \[ U = \frac{1}{2}kx^2 \] - Năng lượng tích lũy dưới dạng thế năng khi vật dao động.
• Động năng: \[ K = \frac{1}{2}mv^2 \] - Năng lượng mà vật có được do chuyển động.
• Năng lượng toàn phần: \[ E = \frac{1}{2}kA^2 \] - Tổng năng lượng của hệ, luôn được bảo toàn trong dao động điều hòa.

5.2. Mẹo Giải Bài Tập Nhanh

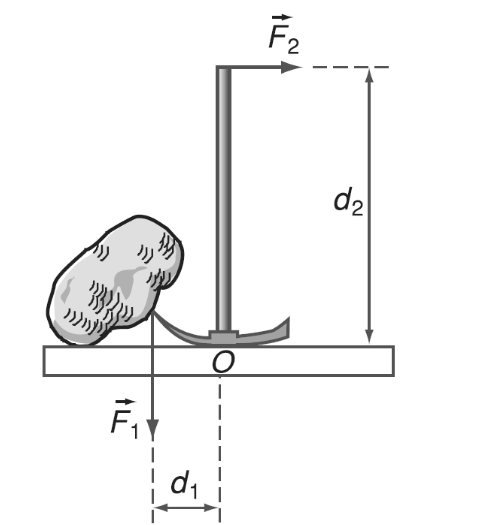
1. Phân tích lực: Khi giải bài tập, trước hết hãy xác định tất cả các lực tác dụng lên vật, đặc biệt là lực kéo về. Vẽ hình minh họa nếu cần để trực quan hóa các lực.
2. Sử dụng công thức phù hợp: Đối với từng loại bài tập, hãy chọn công thức phù hợp. Ví dụ, nếu đề bài yêu cầu tính vận tốc tại một vị trí nhất định, sử dụng công thức vận tốc liên quan đến li độ tại vị trí đó.
3. Chú ý đến pha ban đầu: Pha ban đầu \(\phi\) là yếu tố quan trọng trong các bài toán liên quan đến thời gian hoặc vị trí đặc biệt. Xác định giá trị \(\phi\) chính xác sẽ giúp bạn giải bài tập chính xác hơn.
4. Kiểm tra đơn vị: Đảm bảo rằng các đại lượng bạn sử dụng đều thống nhất về đơn vị (ví dụ: đơn vị lực là Newton, đơn vị khối lượng là kg, đơn vị thời gian là giây).
5. Áp dụng nguyên lý bảo toàn năng lượng: Trong nhiều bài toán, việc áp dụng nguyên lý bảo toàn năng lượng sẽ giúp bạn tìm ra mối liên hệ giữa các đại lượng và dễ dàng tìm ra đáp án.

Dưới đây là tổng hợp các bài tập và đề thi mẫu về hợp lực tác dụng lên vật dao động điều hòa. Những bài tập này được phân chia theo các mức độ khác nhau, từ cơ bản đến nâng cao, nhằm giúp học sinh nắm vững kiến thức và luyện tập hiệu quả.

6.1. Đề thi mẫu về hợp lực trong dao động điều hòa

• Đề thi 1: Tính hợp lực tác dụng lên vật tại vị trí biên và tại vị trí cân bằng trong dao động điều hòa. Sử dụng các giá trị cụ thể của biên độ, tần số góc và khối lượng vật.
• Đề thi 2: Xác định thời điểm lực kéo về đạt giá trị cực đại trong một chu kỳ dao động điều hòa và tính giá trị này.
• Đề thi 3: Cho một vật dao động điều hòa với phương trình \( x = A \cos(\omega t + \varphi) \). Hãy xác định lực tác dụng lên vật tại các thời điểm \( t = 0 \), \( t = T/4 \), \( t = T/2 \), và \( t = 3T/4 \).

6.2. Các bài tập tự luyện theo từng mức độ

6.2.1. Mức độ cơ bản

1. Vật có khối lượng \( m = 0,5 \, \text{kg} \) dao động điều hòa với biên độ \( A = 5 \, \text{cm} \) và tần số góc \( \omega = 10 \, \text{rad/s} \). Tính lực tác dụng lên vật khi nó ở vị trí có li độ \( x = 3 \, \text{cm} \).
2. Một vật dao động điều hòa có độ cứng của lò xo \( k = 100 \, \text{N/m} \). Hãy xác định lực kéo về tại vị trí có li độ bằng 2/3 biên độ.

6.2.2. Mức độ trung bình

1. Cho một vật dao động điều hòa với phương trình \( x = 4 \cos(2\pi t + \pi/3) \, \text{cm} \). Tính lực tác dụng lên vật tại thời điểm \( t = 1 \, \text{s} \).
2. Một vật nặng dao động điều hòa với phương trình \( x = 0,05 \cos(5t + \pi/4) \, \text{m} \). Tìm giá trị lực kéo về tại thời điểm vận tốc bằng 0.

6.2.3. Mức độ nâng cao

1. Một vật có khối lượng 0,2 kg dao động điều hòa với tần số 5 Hz. Tính giá trị cực đại của lực kéo về và xác định tại những thời điểm nào trong chu kỳ dao động thì lực này bằng một nửa giá trị cực đại.
2. Một hệ dao động gồm một lò xo có độ cứng \( k = 50 \, \text{N/m} \) và một vật có khối lượng 0,4 kg. Hãy xác định khoảng thời gian trong một chu kỳ dao động khi lực kéo về có giá trị dương và so sánh với khoảng thời gian lực kéo về có giá trị âm.

Những bài tập và đề thi mẫu này không chỉ giúp học sinh củng cố kiến thức lý thuyết mà còn nâng cao khả năng vận dụng và giải quyết các bài toán thực tiễn liên quan đến dao động điều hòa. Chúc các bạn học tập tốt và đạt kết quả cao trong các kỳ thi!

Để nắm vững kiến thức về hợp lực tác dụng lên vật dao động điều hòa, bạn có thể tham khảo các tài liệu sau đây:

7.1. Sách giáo khoa và tài liệu nâng cao

• Sách giáo khoa Vật lý 12: Đây là nguồn tài liệu cơ bản, cung cấp những kiến thức nền tảng về dao động điều hòa, bao gồm cả hợp lực tác dụng lên vật. Bạn có thể tìm thấy lý thuyết, ví dụ và bài tập có lời giải chi tiết.
• Bài giảng Vật lý nâng cao: Các bài giảng nâng cao này sẽ cung cấp thêm những bài tập khó hơn, giúp bạn rèn luyện khả năng giải quyết các bài toán phức tạp liên quan đến hợp lực trong dao động điều hòa.
• Tài liệu tự học: Sử dụng các tài liệu tự học từ các nguồn uy tín để củng cố và mở rộng kiến thức. Ví dụ, bạn có thể tham khảo các tài liệu từ hoặc .

7.2. Website và nền tảng học trực tuyến

• Onluyen.vn: Nền tảng này cung cấp hàng trăm bài tập về dao động điều hòa, bao gồm cả các bài tập về hợp lực, với đáp án chi tiết. Bạn có thể luyện tập theo từng mức độ để nâng cao kỹ năng.
• SHub.edu.vn: Đây là một nền tảng học tập trực tuyến với các bài giảng, bài tập và đề thi mẫu, đặc biệt hữu ích cho học sinh lớp 12 chuẩn bị cho kỳ thi đại học.
• Hệ thống bài giảng trực tuyến: Ngoài ra, bạn có thể tìm các bài giảng video trên YouTube hoặc các website giáo dục khác để bổ sung kiến thức từ các thầy cô uy tín trong lĩnh vực vật lý.

Việc kết hợp giữa sách giáo khoa, tài liệu nâng cao và các nền tảng học trực tuyến sẽ giúp bạn nắm vững lý thuyết cũng như thành thạo kỹ năng giải quyết các bài toán về hợp lực trong dao động điều hòa.