Tính hợp lực: Hiểu rõ và ứng dụng hiệu quả trong thực tiễn

Tính hợp lực là quá trình tính toán và xác định lực tổng hợp từ hai hay nhiều lực thành phần tác dụng lên một vật. Trong vật lý, khái niệm này giúp xác định hướng và độ lớn của lực kết quả tác động lên vật thể.

Để tính hợp lực, ta sử dụng quy tắc hình bình hành hoặc các công thức đặc biệt tùy thuộc vào trường hợp cụ thể:

• Trường hợp 1: Hai lực \( \vec{F_1} \) và \( \vec{F_2} \) đồng quy và tạo với nhau góc \( \alpha \), độ lớn hợp lực \( \vec{F} \) được tính bằng công thức: \[ F = \sqrt{F_1^2 + F_2^2 + 2F_1F_2\cos\alpha} \]
• Trường hợp 2: Nếu hai lực cùng phương, cùng chiều thì hợp lực là tổng của hai lực: \[ F = F_1 + F_2 \]
• Trường hợp 3: Nếu hai lực ngược chiều thì hợp lực là hiệu của hai lực: \[ F = |F_1 - F_2| \]

1. Bài tập 1: Cho hai lực đồng quy có độ lớn là 8 N và 6 N. Tính hợp lực của hai lực này khi góc giữa chúng là 60°.
2. Bài tập 2: Một vật nằm yên dưới tác dụng của ba lực: \( \vec{F_1} \), \( \vec{F_2} \), và \( \vec{F_3} \). Nếu biết \( \vec{F_1} = 10 \) N, \( \vec{F_2} = 15 \) N, và \( \vec{F_3} \) có phương vuông góc với \( \vec{F_1} \) và \( \vec{F_2} \), hãy tính độ lớn của \( \vec{F_3} \) để vật cân bằng.

Trong thực tế, tính hợp lực được ứng dụng trong nhiều lĩnh vực như xây dựng, cơ khí, và kỹ thuật. Việc tính toán hợp lực giúp xác định cách lực tác dụng lên các cấu trúc, đảm bảo chúng có thể chịu đựng các lực tác động mà không bị biến dạng hay hư hỏng.

Để tính hợp lực, ta sử dụng quy tắc hình bình hành hoặc các công thức đặc biệt tùy thuộc vào trường hợp cụ thể:

• Trường hợp 1: Hai lực \( \vec{F_1} \) và \( \vec{F_2} \) đồng quy và tạo với nhau góc \( \alpha \), độ lớn hợp lực \( \vec{F} \) được tính bằng công thức: \[ F = \sqrt{F_1^2 + F_2^2 + 2F_1F_2\cos\alpha} \]
• Trường hợp 2: Nếu hai lực cùng phương, cùng chiều thì hợp lực là tổng của hai lực: \[ F = F_1 + F_2 \]
• Trường hợp 3: Nếu hai lực ngược chiều thì hợp lực là hiệu của hai lực: \[ F = |F_1 - F_2| \]

1. Bài tập 1: Cho hai lực đồng quy có độ lớn là 8 N và 6 N. Tính hợp lực của hai lực này khi góc giữa chúng là 60°.
2. Bài tập 2: Một vật nằm yên dưới tác dụng của ba lực: \( \vec{F_1} \), \( \vec{F_2} \), và \( \vec{F_3} \). Nếu biết \( \vec{F_1} = 10 \) N, \( \vec{F_2} = 15 \) N, và \( \vec{F_3} \) có phương vuông góc với \( \vec{F_1} \) và \( \vec{F_2} \), hãy tính độ lớn của \( \vec{F_3} \) để vật cân bằng.

Trong thực tế, tính hợp lực được ứng dụng trong nhiều lĩnh vực như xây dựng, cơ khí, và kỹ thuật. Việc tính toán hợp lực giúp xác định cách lực tác dụng lên các cấu trúc, đảm bảo chúng có thể chịu đựng các lực tác động mà không bị biến dạng hay hư hỏng.

1. Bài tập 1: Cho hai lực đồng quy có độ lớn là 8 N và 6 N. Tính hợp lực của hai lực này khi góc giữa chúng là 60°.
2. Bài tập 2: Một vật nằm yên dưới tác dụng của ba lực: \( \vec{F_1} \), \( \vec{F_2} \), và \( \vec{F_3} \). Nếu biết \( \vec{F_1} = 10 \) N, \( \vec{F_2} = 15 \) N, và \( \vec{F_3} \) có phương vuông góc với \( \vec{F_1} \) và \( \vec{F_2} \), hãy tính độ lớn của \( \vec{F_3} \) để vật cân bằng.

Trong thực tế, tính hợp lực được ứng dụng trong nhiều lĩnh vực như xây dựng, cơ khí, và kỹ thuật. Việc tính toán hợp lực giúp xác định cách lực tác dụng lên các cấu trúc, đảm bảo chúng có thể chịu đựng các lực tác động mà không bị biến dạng hay hư hỏng.

Trong thực tế, tính hợp lực được ứng dụng trong nhiều lĩnh vực như xây dựng, cơ khí, và kỹ thuật. Việc tính toán hợp lực giúp xác định cách lực tác dụng lên các cấu trúc, đảm bảo chúng có thể chịu đựng các lực tác động mà không bị biến dạng hay hư hỏng.

Lực là một đại lượng vật lý mô tả sự tương tác giữa các vật thể. Lực có khả năng làm thay đổi trạng thái chuyển động của vật hoặc làm biến dạng vật. Mỗi lực có ba đặc trưng chính:

• Độ lớn: Được đo bằng đơn vị Newton (N), độ lớn của lực thể hiện mức độ mạnh yếu của sự tương tác.
• Phương và chiều: Lực có phương và chiều xác định, biểu thị hướng tác động của lực lên vật thể.
• Điểm đặt: Vị trí mà lực tác động lên vật thể, ảnh hưởng đến khả năng làm vật chuyển động hoặc biến dạng.

Công thức tổng quát để biểu diễn lực là:

\[\vec{F} = m \cdot \vec{a}\]

Trong đó:

• \(\vec{F}\) là lực tác động lên vật (N).
• \(m\) là khối lượng của vật (kg).
• \(\vec{a}\) là gia tốc của vật do lực gây ra (m/s²).

Đơn vị đo của lực là Newton (N), và 1 Newton được định nghĩa là lực cần thiết để làm cho một vật có khối lượng 1 kg gia tốc 1 m/s².

Tổng hợp lực là quá trình thay thế hai hay nhiều lực tác dụng đồng thời lên một vật bằng một lực duy nhất sao cho lực này gây ra tác dụng tương đương với các lực đã cho. Lực duy nhất đó gọi là hợp lực.

2.1 Định nghĩa tổng hợp lực

Tổng hợp lực là việc tìm một lực duy nhất (hợp lực) thay thế cho nhiều lực cùng tác dụng lên một vật, sao cho tác dụng của hợp lực tương đương với tác dụng của các lực thành phần.

2.2 Hợp lực và cách xác định hợp lực

Hợp lực của hai lực đồng quy \(\vec{F}_1\) và \(\vec{F}_2\) có thể được xác định bằng công thức:

\[\vec{F}_{\text{hợp}} = \vec{F}_1 + \vec{F}_2\]

Trong trường hợp hai lực này có cùng phương, hợp lực sẽ là tổng đại số của các lực:

\[F_{\text{hợp}} = F_1 + F_2\]

Nếu hai lực có phương khác nhau, hợp lực sẽ được xác định bằng quy tắc hình bình hành hoặc bằng cách phân tích lực thành các thành phần theo trục tọa độ.

2.3 Quy tắc hình bình hành trong tổng hợp lực

Quy tắc hình bình hành là phương pháp phổ biến để xác định hợp lực khi hai lực \(\vec{F}_1\) và \(\vec{F}_2\) có phương không cùng chiều. Để áp dụng quy tắc này:

1. Vẽ hai vectơ lực \(\vec{F}_1\) và \(\vec{F}_2\) xuất phát từ cùng một điểm.
2. Vẽ các đường song song với \(\vec{F}_1\) và \(\vec{F}_2\) để tạo thành một hình bình hành.
3. Đường chéo của hình bình hành xuất phát từ điểm gốc chung chính là vectơ hợp lực \(\vec{F}_{\text{hợp}}\).

2.4 Các bài tập ví dụ về tổng hợp lực

Dưới đây là một số bài tập ví dụ về tổng hợp lực:

• Bài tập 1: Tính hợp lực của hai lực đồng quy cùng phương có độ lớn lần lượt là 5 N và 10 N.
• Bài tập 2: Tính hợp lực của hai lực đồng quy tạo với nhau một góc 60 độ, có độ lớn lần lượt là 8 N và 6 N.
• Bài tập 3: Sử dụng quy tắc hình bình hành để xác định hợp lực khi hai lực \(\vec{F}_1 = 3\) N và \(\vec{F}_2 = 4\) N tạo với nhau một góc 90 độ.

Phân tích lực là quá trình tách một lực thành hai hay nhiều lực thành phần có tác dụng tương đương với lực ban đầu. Điều này giúp dễ dàng hơn trong việc nghiên cứu và giải quyết các bài toán liên quan đến lực.

3.1 Khái niệm và ý nghĩa của phân tích lực

Phân tích lực là kỹ thuật quan trọng trong cơ học, giúp ta hiểu rõ hơn về tác dụng của lực lên vật thể. Bằng cách phân tích lực, ta có thể xác định các lực thành phần tác dụng theo các hướng khác nhau, từ đó đưa ra giải pháp tối ưu cho các bài toán kỹ thuật.

3.2 Quy trình phân tích lực

Quy trình phân tích lực bao gồm các bước sau:

1. Xác định lực cần phân tích: Lực cần phân tích thường được biểu diễn dưới dạng vectơ.
2. Chọn hệ trục tọa độ: Chọn một hệ trục tọa độ phù hợp (thường là trục ngang và trục dọc) để dễ dàng phân tích các thành phần lực.
3. Phân tích lực thành các thành phần: Sử dụng các công thức lượng giác để phân tích lực theo các trục tọa độ đã chọn. Ví dụ, với lực \(\vec{F}\) tạo với trục hoành một góc \(\alpha\), ta có:
• Thành phần lực theo trục \(x\): \(F_x = F \cdot \cos(\alpha)\)
• Thành phần lực theo trục \(y\): \(F_y = F \cdot \sin(\alpha)\)

3.3 Ứng dụng của phân tích lực trong đời sống

Phân tích lực được ứng dụng rộng rãi trong nhiều lĩnh vực của đời sống và kỹ thuật, bao gồm:

• Kỹ thuật xây dựng: Xác định các lực tác dụng lên các cấu trúc xây dựng như cầu, nhà cao tầng, giúp đảm bảo an toàn và ổn định.
• Thiết kế máy móc: Phân tích lực trong các cơ cấu máy móc để tối ưu hóa hoạt động và tăng tuổi thọ của thiết bị.
• Thể thao: Giúp các vận động viên tối ưu hóa kỹ thuật, cải thiện hiệu suất thi đấu thông qua việc hiểu rõ hơn về lực tác động lên cơ thể.

Cân bằng của vật là trạng thái khi vật không thay đổi vị trí hoặc không bị biến dạng dưới tác dụng của các lực tác động lên nó. Điều kiện để một vật cân bằng được xác định bởi sự cân bằng của cả lực và mômen lực tác dụng lên vật.

4.1 Khái niệm cân bằng lực

Một vật ở trạng thái cân bằng khi tổng hợp lực tác dụng lên nó bằng không. Khi đó, vật sẽ không bị dịch chuyển hay thay đổi trạng thái chuyển động.

Điều này có thể biểu diễn bằng công thức:

\[\sum \vec{F} = 0\]

Trong đó, \(\sum \vec{F}\) là tổng các lực tác dụng lên vật.

4.2 Điều kiện cần và đủ để một vật cân bằng

Để một vật ở trạng thái cân bằng, cần thỏa mãn đồng thời hai điều kiện sau:

1. Điều kiện thứ nhất (cân bằng lực): Tổng các lực tác dụng lên vật phải bằng không.

\[\sum \vec{F} = 0\]

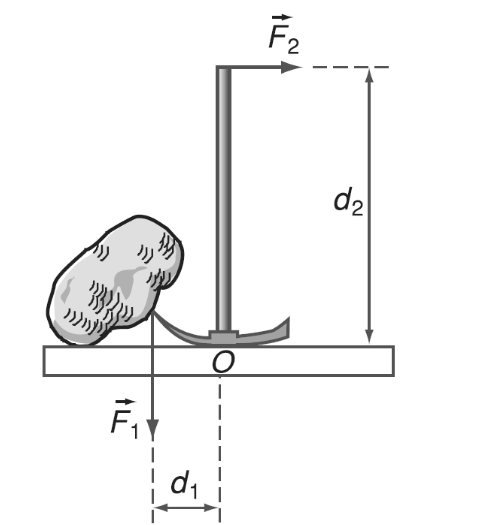
2. Điều kiện thứ hai (cân bằng mômen): Tổng mômen của các lực đối với một điểm bất kỳ phải bằng không.

\[\sum \vec{M} = 0\]

Trong đó, \(\sum \vec{M}\) là tổng mômen lực tác dụng lên vật.

4.3 Cách xác định trạng thái cân bằng

Để xác định trạng thái cân bằng của vật, ta thực hiện các bước sau:

1. Xác định tất cả các lực tác dụng lên vật: Xác định điểm đặt, phương, chiều và độ lớn của các lực này.
2. Tính tổng hợp lực: Sử dụng phương pháp tổng hợp lực để tính tổng hợp lực tác dụng lên vật. Nếu tổng hợp lực bằng không, điều kiện cân bằng lực được thỏa mãn.
3. Tính tổng mômen lực: Chọn một điểm bất kỳ làm gốc tính mômen. Tính tổng mômen của các lực đối với điểm này. Nếu tổng mômen bằng không, điều kiện cân bằng mômen được thỏa mãn.

Nếu cả hai điều kiện cân bằng lực và cân bằng mômen đều được thỏa mãn, vật sẽ ở trạng thái cân bằng.

Việc hiểu rõ về tính hợp lực không chỉ quan trọng trong học tập mà còn có nhiều ứng dụng thực tế trong cuộc sống và kỹ thuật. Dưới đây là một số bài tập mẫu và các ứng dụng phổ biến của tính hợp lực.

5.1 Bài tập trắc nghiệm tổng hợp lực

• Bài tập 1: Hai lực đồng quy \(\vec{F}_1 = 5\) N và \(\vec{F}_2 = 12\) N tạo với nhau một góc 90°. Tính hợp lực của chúng.
• Bài tập 2: Hai lực có phương song song ngược chiều, lực thứ nhất có độ lớn 8 N, lực thứ hai có độ lớn 5 N. Xác định hợp lực.
• Bài tập 3: Một vật chịu tác dụng của ba lực: \(\vec{F}_1 = 3\) N theo hướng Đông, \(\vec{F}_2 = 4\) N theo hướng Bắc, và \(\vec{F}_3 = 5\) N theo hướng Tây. Tính hợp lực tác dụng lên vật.

5.2 Bài tập phân tích lực

• Bài tập 1: Phân tích lực \(\vec{F} = 10\) N tạo với trục hoành một góc 30° thành hai thành phần lực theo trục \(x\) và \(y\).
• Bài tập 2: Một vật được treo bằng hai dây. Phân tích các lực trong hệ để tìm ra lực căng của mỗi dây.
• Bài tập 3: Một người đẩy một vật theo phương xiên với góc 45° so với mặt phẳng ngang. Phân tích lực tác dụng lên vật theo phương ngang và phương thẳng đứng.

5.3 Ứng dụng tính hợp lực trong kỹ thuật và đời sống

Tính hợp lực là cơ sở cho nhiều ứng dụng trong kỹ thuật và đời sống thực tế:

• Xây dựng: Tính hợp lực được áp dụng trong việc thiết kế và tính toán độ bền của các cấu trúc xây dựng như cầu, tòa nhà, và các kết cấu chịu lực khác.
• Thiết kế máy móc: Trong các hệ thống máy móc, tính hợp lực giúp xác định và phân phối lực để tối ưu hóa hoạt động và đảm bảo an toàn cho thiết bị.
• Thể thao: Hiểu rõ về hợp lực giúp các vận động viên tối ưu hóa kỹ thuật, đặc biệt trong các môn thể thao đòi hỏi sự kết hợp lực như cử tạ, đua xe đạp, và nhảy xa.