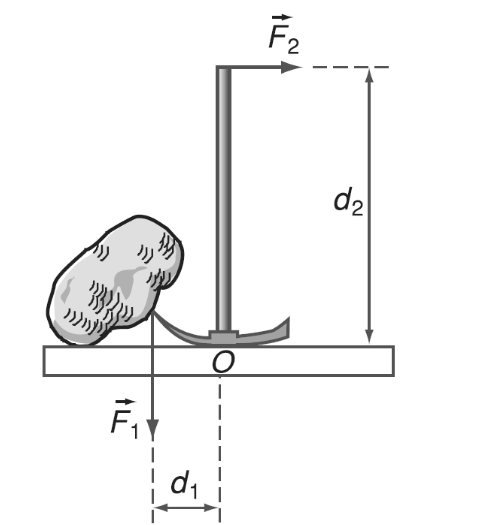
Chủ đề tổng hợp lực là: "Tổng hợp lực là" là một khái niệm cơ bản nhưng vô cùng quan trọng trong vật lý, ảnh hưởng lớn đến nhiều lĩnh vực từ kỹ thuật đến đời sống. Bài viết này sẽ cung cấp cái nhìn toàn diện về khái niệm này, bao gồm các phương pháp tổng hợp lực, công thức tính toán, và những ứng dụng thực tiễn để bạn dễ dàng áp dụng trong thực tế.
Mục lục
Tổng hợp lực là gì?
Tổng hợp lực là một khái niệm cơ bản trong vật lý, đề cập đến việc kết hợp nhiều lực tác động lên một vật thể thành một lực duy nhất có cùng tác dụng như tất cả các lực thành phần đó. Lực này được gọi là "hợp lực". Quá trình này có thể thực hiện bằng nhiều phương pháp khác nhau, phụ thuộc vào hướng và độ lớn của các lực thành phần.
Phương pháp tổng hợp lực
- Quy tắc hình bình hành: Khi hai lực đồng quy được biểu diễn bằng hai cạnh của một hình bình hành, đường chéo kẻ từ điểm đồng quy sẽ biểu diễn hợp lực của chúng.
- Quy tắc hình học: Hợp lực của hai lực đồng quy cũng có thể được xác định bằng cách sử dụng định lý Pythagore khi hai lực vuông góc với nhau, hoặc bằng công thức tổng quát khi chúng tạo thành một góc bất kỳ.
Công thức tổng hợp lực
Nếu hai lực \( \vec{F_1} \) và \( \vec{F_2} \) tạo với nhau một góc \( \alpha \), hợp lực \( \vec{F} \) của chúng được tính bằng công thức:
\[ \vec{F} = \sqrt{F_1^2 + F_2^2 + 2F_1F_2\cos\alpha} \]
Nếu hai lực cùng phương và cùng chiều, hợp lực sẽ bằng tổng của chúng:
\[ F = F_1 + F_2 \]
Nếu hai lực cùng phương nhưng ngược chiều, hợp lực sẽ bằng hiệu độ lớn của hai lực:
\[ F = |F_1 - F_2| \]
Nếu hai lực vuông góc, hợp lực được tính bằng:
\[ F = \sqrt{F_1^2 + F_2^2} \]
Ứng dụng của tổng hợp lực
Trong thực tế, tổng hợp lực có nhiều ứng dụng quan trọng trong kỹ thuật, xây dựng, giao thông và đời sống hàng ngày. Ví dụ:
- Trong xây dựng: Tổng hợp lực được dùng để tính toán lực tác động lên các kết cấu như dầm, cột trong công trình.
- Trong giao thông: Tối ưu hóa lực kéo của các phương tiện như ô tô, máy bay, tàu thủy để đảm bảo hiệu suất hoạt động tốt nhất.
- Trong thể thao: Sử dụng khái niệm hợp lực để tối ưu hóa hiệu suất vận động và giảm thiểu chấn thương trong các môn thể thao như chạy bộ, đua xe đạp, bơi lội.
Bài tập minh họa
| Bài tập | Lời giải |
|---|---|
| Hai lực có độ lớn lần lượt là 3N và 4N hợp với nhau một góc vuông. Tính hợp lực của chúng. | \[ F = \sqrt{3^2 + 4^2} = 5 \, \text{N} \] |
| Hai lực có độ lớn là 7N và 10N tạo với nhau một góc 60°. Tính hợp lực của chúng. | \[ F = \sqrt{7^2 + 10^2 + 2 \times 7 \times 10 \times \cos60^\circ} = \sqrt{49 + 100 + 70} = \sqrt{219} \approx 14.8 \, \text{N} \] |

.png)
1. Khái niệm tổng hợp lực
Tổng hợp lực là quá trình kết hợp nhiều lực tác dụng lên cùng một vật thể thành một lực duy nhất, được gọi là hợp lực. Lực này có tác dụng tương đương với tác dụng của tất cả các lực thành phần cộng lại. Trong vật lý, việc tổng hợp lực giúp chúng ta dễ dàng phân tích và dự đoán chuyển động của vật thể dưới tác động của nhiều lực khác nhau.
Khi hai lực đồng quy tác động lên một vật thể, chúng có thể được tổng hợp lại thành một lực duy nhất theo quy tắc hình bình hành. Điều này có nghĩa là ta vẽ hai vector lực xuất phát từ một điểm, và hợp lực sẽ là vector đường chéo của hình bình hành được tạo bởi hai vector lực đó.
Công thức tổng hợp lực khi hai lực \( \vec{F_1} \) và \( \vec{F_2} \) tạo với nhau một góc \( \alpha \) là:
\[ \vec{F} = \sqrt{F_1^2 + F_2^2 + 2F_1F_2\cos\alpha} \]
Nếu hai lực cùng phương và cùng chiều, hợp lực sẽ là tổng đại số của hai lực:
\[ F = F_1 + F_2 \]
Nếu hai lực cùng phương nhưng ngược chiều, hợp lực sẽ là hiệu đại số của chúng:
\[ F = |F_1 - F_2| \]
Trường hợp hai lực vuông góc với nhau, hợp lực sẽ được tính bằng định lý Pythagoras:
\[ F = \sqrt{F_1^2 + F_2^2} \]
Việc hiểu rõ khái niệm và công thức tổng hợp lực giúp chúng ta dễ dàng áp dụng vào các bài toán vật lý cũng như các ứng dụng thực tế trong đời sống và kỹ thuật.
2. Các phương pháp tổng hợp lực
Có nhiều phương pháp để tổng hợp các lực tác động lên một vật thể thành một lực duy nhất. Mỗi phương pháp đều có ưu điểm riêng và áp dụng tùy thuộc vào tình huống cụ thể. Dưới đây là các phương pháp phổ biến được sử dụng trong vật lý.
2.1. Phương pháp hình bình hành
Đây là phương pháp trực quan và dễ hiểu nhất để tổng hợp hai lực đồng quy. Khi hai lực \( \vec{F_1} \) và \( \vec{F_2} \) tác động lên một điểm, ta vẽ hai vector đại diện cho hai lực này xuất phát từ cùng một điểm. Sau đó, ta vẽ một hình bình hành mà \( \vec{F_1} \) và \( \vec{F_2} \) là hai cạnh liền kề. Đường chéo của hình bình hành chính là hợp lực \( \vec{F} \) cần tìm.
2.2. Phương pháp hình học
Phương pháp này sử dụng các công thức hình học để tính hợp lực, đặc biệt hiệu quả khi hai lực vuông góc hoặc tạo với nhau một góc bất kỳ.
- Trường hợp hai lực vuông góc: Hợp lực được tính bằng định lý Pythagoras:
\[ F = \sqrt{F_1^2 + F_2^2} \]
- Trường hợp hai lực tạo thành góc bất kỳ: Hợp lực được tính bằng công thức:
\[ F = \sqrt{F_1^2 + F_2^2 + 2F_1F_2\cos\alpha} \]
Ở đây, \( \alpha \) là góc giữa hai lực \( \vec{F_1} \) và \( \vec{F_2} \).
2.3. Phương pháp đại số
Phương pháp này thường được sử dụng khi hai lực có cùng phương hoặc ngược chiều. Các bước thực hiện bao gồm:
- Hai lực cùng phương và cùng chiều: Tổng hợp lực bằng cách cộng độ lớn của hai lực:
\[ F = F_1 + F_2 \]
- Hai lực cùng phương nhưng ngược chiều: Hợp lực bằng hiệu đại số của hai lực:
\[ F = |F_1 - F_2| \]
Những phương pháp trên đều giúp ta xác định chính xác hợp lực trong các tình huống cụ thể, từ đó dự đoán được chuyển động và tác dụng của lực lên vật thể.

3. Công thức tổng hợp lực
Công thức tổng hợp lực giúp chúng ta tính toán hợp lực khi có nhiều lực tác động đồng thời lên một vật thể. Tùy vào hướng và độ lớn của các lực, công thức sẽ thay đổi để đảm bảo tính chính xác trong quá trình tổng hợp. Dưới đây là các công thức quan trọng và cách sử dụng chúng trong từng trường hợp cụ thể.
3.1. Tổng hợp hai lực đồng quy tạo thành góc bất kỳ
Khi hai lực \( \vec{F_1} \) và \( \vec{F_2} \) tạo với nhau một góc \( \alpha \), hợp lực \( \vec{F} \) được tính bằng công thức:
\[ \vec{F} = \sqrt{F_1^2 + F_2^2 + 2F_1F_2\cos\alpha} \]
Trong đó:
- \( F_1, F_2 \) là độ lớn của hai lực.
- \( \alpha \) là góc giữa hai lực.
- \( F \) là độ lớn của hợp lực.
3.2. Tổng hợp hai lực đồng quy cùng phương
- Khi hai lực cùng chiều: Hợp lực là tổng đại số của hai lực:
\[ F = F_1 + F_2 \]
- Khi hai lực ngược chiều: Hợp lực là hiệu đại số của hai lực:
\[ F = |F_1 - F_2| \]
3.3. Tổng hợp hai lực vuông góc
Khi hai lực vuông góc với nhau, hợp lực được tính bằng định lý Pythagoras:
\[ F = \sqrt{F_1^2 + F_2^2} \]
3.4. Công thức tổng quát
Công thức tổng quát cho việc tổng hợp nhiều lực đồng quy tác động lên một vật thể là:
\[ \vec{F_{hợp}} = \sum \vec{F_i} \]
Trong đó, \( \vec{F_{hợp}} \) là hợp lực, còn \( \sum \vec{F_i} \) là tổng vector của tất cả các lực tác dụng lên vật thể.
Việc nắm vững các công thức trên giúp chúng ta giải quyết hiệu quả các bài toán về lực trong vật lý và áp dụng chúng vào các tình huống thực tế một cách chính xác.
4. Ứng dụng của tổng hợp lực
Tổng hợp lực không chỉ là một khái niệm cơ bản trong vật lý học mà còn có rất nhiều ứng dụng thực tiễn trong đời sống, kỹ thuật và công nghệ. Dưới đây là một số ví dụ về cách tổng hợp lực được áp dụng trong các lĩnh vực khác nhau.
4.1. Ứng dụng trong đời sống hàng ngày
Trong đời sống, tổng hợp lực giúp chúng ta giải quyết các bài toán thực tế liên quan đến cân bằng và chuyển động. Ví dụ, khi sử dụng một ròng rọc để nâng vật nặng, các lực tác dụng từ dây cáp sẽ được tổng hợp lại để xác định lực cần thiết để nâng vật lên.
4.2. Ứng dụng trong kỹ thuật và công nghệ
Trong lĩnh vực kỹ thuật, tổng hợp lực được ứng dụng rộng rãi trong thiết kế kết cấu, xây dựng cầu, nhà cửa, và các công trình khác. Kỹ sư sử dụng tổng hợp lực để tính toán tải trọng và đảm bảo rằng các công trình có thể chịu được các lực tác động từ môi trường, như gió, động đất, và trọng lực.
4.3. Ứng dụng trong thể thao
Trong thể thao, tổng hợp lực giúp các vận động viên tối ưu hóa hiệu suất. Chẳng hạn, khi một vận động viên nhảy xa, các lực từ chân và tay được tổng hợp lại để tạo ra lực đẩy lớn nhất, giúp vận động viên nhảy xa hơn. Tương tự, trong các môn thể thao như đẩy tạ hay bắn cung, việc tổng hợp lực đúng cách sẽ cải thiện độ chính xác và hiệu quả.
4.4. Ứng dụng trong cơ học
Trong cơ học, tổng hợp lực là cơ sở để phân tích chuyển động của các vật thể dưới tác động của nhiều lực khác nhau. Điều này rất quan trọng trong việc thiết kế và vận hành các máy móc, từ xe cộ, máy bay đến các hệ thống tự động hóa.
Nhờ vào việc nắm vững khái niệm và các phương pháp tổng hợp lực, chúng ta có thể ứng dụng một cách hiệu quả vào nhiều lĩnh vực khác nhau, từ đó cải thiện chất lượng cuộc sống và hiệu suất làm việc.

5. Bài tập và ví dụ minh họa
Để hiểu rõ hơn về khái niệm tổng hợp lực, chúng ta sẽ xem xét một số bài tập và ví dụ minh họa cụ thể. Những bài tập này sẽ giúp bạn áp dụng lý thuyết vào thực tiễn và nắm vững cách tính hợp lực trong các tình huống khác nhau.
5.1. Bài tập 1: Tổng hợp hai lực đồng quy
Giả sử có hai lực \( \vec{F_1} = 5 \, \text{N} \) và \( \vec{F_2} = 7 \, \text{N} \) tác động lên một điểm theo hai phương tạo thành một góc \( 60^\circ \). Tính hợp lực \( \vec{F} \).
Giải: Sử dụng công thức tổng hợp lực khi hai lực tạo thành góc bất kỳ:
\[ \vec{F} = \sqrt{F_1^2 + F_2^2 + 2F_1F_2\cos\alpha} \]
Thay các giá trị vào công thức:
\[ \vec{F} = \sqrt{5^2 + 7^2 + 2 \times 5 \times 7 \times \cos 60^\circ} = \sqrt{25 + 49 + 35} = \sqrt{109} \approx 10.44 \, \text{N} \]
5.2. Bài tập 2: Tổng hợp hai lực cùng phương
Hai lực \( \vec{F_1} = 8 \, \text{N} \) và \( \vec{F_2} = 3 \, \text{N} \) cùng tác động lên một vật theo cùng phương và cùng chiều. Tính hợp lực \( \vec{F} \).
Giải: Vì hai lực cùng phương và cùng chiều, hợp lực được tính bằng tổng độ lớn của hai lực:
\[ \vec{F} = F_1 + F_2 = 8 \, \text{N} + 3 \, \text{N} = 11 \, \text{N} \]
5.3. Bài tập 3: Tổng hợp hai lực ngược chiều
Một lực \( \vec{F_1} = 10 \, \text{N} \) tác động lên một vật theo chiều từ trái sang phải, và một lực \( \vec{F_2} = 4 \, \text{N} \) tác động theo chiều ngược lại. Tính hợp lực \( \vec{F} \).
Giải: Do hai lực ngược chiều, hợp lực được tính bằng hiệu đại số của hai lực:
\[ \vec{F} = |F_1 - F_2| = |10 \, \text{N} - 4 \, \text{N}| = 6 \, \text{N} \]
5.4. Ví dụ minh họa trong thực tế
Hãy xem xét một ví dụ trong thực tế: Khi một chiếc tàu đang di chuyển với vận tốc không đổi, các lực tác động lên tàu như lực đẩy của động cơ, lực cản của nước, và lực ma sát với không khí đều đã được tổng hợp lại. Khi các lực này cân bằng nhau, tàu sẽ duy trì vận tốc không đổi. Nếu lực đẩy từ động cơ lớn hơn tổng các lực cản, tàu sẽ tăng tốc.
Những bài tập và ví dụ trên giúp bạn nắm vững cách tính toán và ứng dụng tổng hợp lực trong cả các bài toán lý thuyết lẫn các tình huống thực tế.