Tổng hợp lực là thay thế: Cách tính toán và ứng dụng trong đời sống

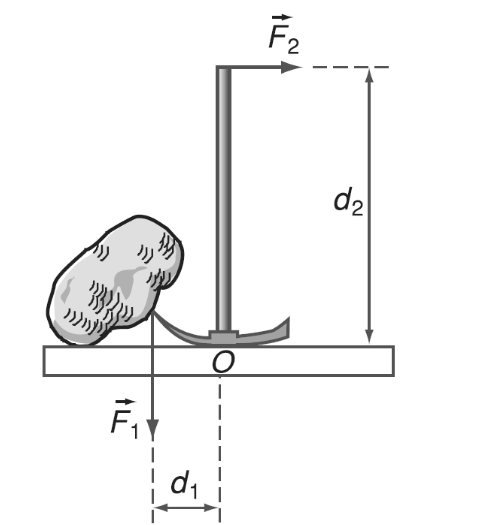
Trong Vật lý, tổng hợp lực là quá trình thay thế các lực tác dụng đồng thời lên một vật bằng một lực duy nhất có tác dụng tương đương với tổng tác dụng của tất cả các lực đó. Lực thay thế này được gọi là hợp lực.

Quy tắc tổng hợp lực

Quy tắc hình bình hành là một phương pháp phổ biến để tìm hợp lực của hai lực đồng quy. Theo quy tắc này:

• Hai lực thành phần được biểu diễn bằng hai cạnh của một hình bình hành.
• Hợp lực chính là đường chéo của hình bình hành đó, xuất phát từ điểm đồng quy.

Ví dụ, nếu hai lực \( \vec{F}_1 \) và \( \vec{F}_2 \) hợp với nhau một góc \( \alpha \), độ lớn của hợp lực \( \vec{F} \) được tính theo công thức:

\[
F = \sqrt{F_1^2 + F_2^2 + 2F_1F_2\cos\alpha}
\]

Ứng dụng thực tiễn

Trong các bài toán thực tiễn, chúng ta thường gặp trường hợp tính hợp lực của các lực đồng quy tác dụng lên một vật. Ví dụ, khi phân tích lực tác dụng lên một vật đặt trên mặt phẳng nghiêng, chúng ta có thể phân tích trọng lực của vật thành hai thành phần: một thành phần song song với mặt phẳng nghiêng và một thành phần vuông góc với mặt phẳng nghiêng.

Bài tập ví dụ

1. Cho hai lực đồng quy có độ lớn \( F_1 = 100N \) và \( F_2 = 80N \), góc giữa chúng là 60°. Tính hợp lực.
2. Một vật có khối lượng 6kg treo bằng hai dây, hãy xác định lực căng của mỗi dây khi góc giữa chúng là 45°.

Nhận xét

Khi góc hợp bởi hai lực thành phần tăng dần từ 0° đến 180°, độ lớn của hợp lực giảm từ giá trị cực đại về giá trị cực tiểu, điều này được thể hiện rõ trong các bài tập phân tích lực. Khả năng nắm vững quy tắc tổng hợp lực giúp ích rất nhiều trong việc giải quyết các bài toán cơ học trong thực tế.

Tổng hợp lực là quá trình thay thế nhiều lực đồng thời tác dụng lên một vật bằng một lực duy nhất, sao cho lực này có cùng tác dụng như tất cả các lực thành phần. Lực này được gọi là hợp lực. Khi các lực cùng tác dụng lên một vật, chúng có thể được cộng gộp lại theo quy tắc hình bình hành.

Để hiểu rõ hơn về tổng hợp lực, chúng ta cần biết rằng các lực có thể được phân tích thành các thành phần và sau đó được tổng hợp lại để tìm hợp lực. Các bước thực hiện tổng hợp lực bao gồm:

1. Xác định các lực thành phần tác dụng lên vật.
2. Xác định hướng và độ lớn của từng lực thành phần.
3. Áp dụng quy tắc hình bình hành để tìm hợp lực. Theo đó, hai lực thành phần được biểu diễn bởi hai cạnh liền kề của một hình bình hành, và đường chéo của hình bình hành chính là hợp lực.

Trong trường hợp đơn giản nhất, khi hai lực \( \vec{F}_1 \) và \( \vec{F}_2 \) có cùng phương, hợp lực được tính bằng tổng đại số của chúng:

\[
\vec{F} = \vec{F}_1 + \vec{F}_2
\]

Trong trường hợp hai lực không cùng phương, hợp lực được tính bằng công thức:

\[
F = \sqrt{F_1^2 + F_2^2 + 2F_1F_2\cos\alpha}
\]

Trong đó, \( \alpha \) là góc giữa hai lực \( \vec{F}_1 \) và \( \vec{F}_2 \). Khi \( \alpha = 0^\circ \), hai lực cùng phương và hợp lực lớn nhất. Khi \( \alpha = 180^\circ \), hai lực ngược phương và hợp lực nhỏ nhất.

Trong Vật lý, phân tích lực là quá trình tách một lực thành hai hay nhiều lực thành phần có tác dụng tương đương. Thông thường, lực được phân tích thành các thành phần theo các trục tọa độ vuông góc với nhau, thường là trục Ox và Oy.

Ví dụ, một lực \( \vec{F} \) tác dụng lên một vật có thể được phân tích thành hai lực thành phần \( \vec{F}_x \) và \( \vec{F}_y \) theo các trục tọa độ như sau:

\[
\vec{F} = \vec{F}_x + \vec{F}_y
\]

Trong đó:

• \( \vec{F}_x = F \cos \theta \): thành phần của lực theo trục Ox.
• \( \vec{F}_y = F \sin \theta \): thành phần của lực theo trục Oy.

Ngược lại với phân tích lực, tổng hợp lực là quá trình kết hợp các lực thành phần để tạo ra một lực duy nhất có tác dụng tương đương. Quy trình tổng hợp lực diễn ra như sau:

1. Xác định các lực thành phần tác dụng lên vật.
2. Sử dụng quy tắc hình bình hành để tìm hợp lực, nếu các lực không cùng phương.
3. Tính hợp lực bằng cách cộng đại số nếu các lực cùng phương.

Công thức tính hợp lực cho hai lực thành phần không cùng phương là:

\[
F = \sqrt{F_x^2 + F_y^2}
\]

Trong đó \( F_x \) và \( F_y \) là độ lớn của các lực thành phần theo trục Ox và Oy. Tổng hợp lực là bước cần thiết để đơn giản hóa các bài toán liên quan đến nhiều lực tác dụng đồng thời lên một vật, giúp chúng ta dễ dàng xác định hướng và độ lớn của lực tổng hợp.

Trong phần này, chúng ta sẽ thực hành các bài tập về tổng hợp lực để hiểu rõ hơn về cách tính toán và áp dụng các quy tắc đã học. Các bài tập dưới đây sẽ giúp bạn nắm vững kỹ năng phân tích và tổng hợp lực qua các tình huống cụ thể.

1. Bài tập 1: Hai lực đồng quy \( \vec{F}_1 \) và \( \vec{F}_2 \) có độ lớn lần lượt là 50N và 80N, hợp với nhau một góc \( 60^\circ \). Tính độ lớn của hợp lực \( \vec{F} \).

   Hướng dẫn:

   • Sử dụng công thức tổng hợp lực: \[ F = \sqrt{F_1^2 + F_2^2 + 2F_1F_2\cos\alpha} \]
   • Thay các giá trị vào: \[ F = \sqrt{50^2 + 80^2 + 2 \times 50 \times 80 \times \cos 60^\circ} \]
   • Tính toán và tìm ra kết quả.

2. Bài tập 2: Một vật có khối lượng 5kg đặt trên mặt phẳng nghiêng với góc nghiêng \( 30^\circ \). Tính thành phần của trọng lực song song và vuông góc với mặt phẳng nghiêng.

   Hướng dẫn:

   • Xác định trọng lực của vật: \( \vec{P} = mg = 5 \times 9.8 = 49N \).
   • Thành phần song song với mặt phẳng nghiêng: \[ P_{\parallel} = P \sin \theta = 49 \sin 30^\circ \]
   • Thành phần vuông góc với mặt phẳng nghiêng: \[ P_{\perp} = P \cos \theta = 49 \cos 30^\circ \]

3. Bài tập 3: Tính hợp lực của ba lực đồng quy \( \vec{F}_1 = 40N \), \( \vec{F}_2 = 50N \) và \( \vec{F}_3 = 30N \) với các góc giữa chúng là \( 120^\circ \).

   Hướng dẫn:

   • Phân tích lực thành các thành phần trên các trục Ox và Oy.
   • Tính tổng các thành phần lực trên mỗi trục.
   • Sử dụng công thức tổng hợp lực để tìm độ lớn của hợp lực.

Việc giải các bài tập trên giúp củng cố kiến thức về tổng hợp lực và phân tích lực, đồng thời ứng dụng chúng vào các tình huống cụ thể, từ đơn giản đến phức tạp. Hãy chắc chắn bạn hiểu từng bước giải để áp dụng linh hoạt trong các bài toán khác nhau.

Tổng hợp lực không chỉ là một khái niệm lý thuyết trong vật lý, mà còn có nhiều ứng dụng thực tế trong đời sống hàng ngày. Dưới đây là một số lĩnh vực mà tổng hợp lực đóng vai trò quan trọng:

4.1 Ứng dụng trong xây dựng và kiến trúc

Trong xây dựng và kiến trúc, việc tổng hợp lực được áp dụng để tính toán các lực tác động lên các cấu trúc như tòa nhà, cầu, và các công trình khác. Ví dụ, trong việc thiết kế cầu, kỹ sư phải tính toán tổng hợp lực từ gió, trọng lực, và tải trọng động để đảm bảo cầu có thể chịu được tất cả các tác động mà không bị phá hủy.

4.2 Ứng dụng trong công nghiệp và máy móc

Trong ngành công nghiệp, tổng hợp lực được sử dụng để đảm bảo rằng các máy móc hoạt động hiệu quả và an toàn. Các kỹ sư cần tổng hợp các lực tác động lên các bộ phận máy móc để đảm bảo rằng chúng hoạt động ổn định và không gây ra các vấn đề như rung động quá mức hay hỏng hóc.

4.3 Ứng dụng trong thể thao và giải trí

Trong lĩnh vực thể thao, tổng hợp lực giúp các huấn luyện viên và vận động viên tối ưu hóa kỹ thuật và cải thiện hiệu suất. Ví dụ, trong bóng đá, lực từ chân cầu thủ được tổng hợp với lực từ động tác chuyển động cơ thể để tạo ra cú sút mạnh mẽ và chính xác.

Tổng hợp lực là một công cụ hữu ích trong việc hiểu và ứng dụng các nguyên lý vật lý vào thực tế. Từ xây dựng, sản xuất công nghiệp đến thể thao, khả năng phân tích và tổng hợp lực không chỉ giúp cải thiện hiệu suất mà còn đảm bảo an toàn và hiệu quả trong các hoạt động hàng ngày.

Việc tổng hợp lực đòi hỏi độ chính xác cao và sự hỗ trợ của các công cụ và phần mềm là điều không thể thiếu. Dưới đây là một số công cụ và phần mềm phổ biến được sử dụng trong lĩnh vực này:

5.1 Các phần mềm mô phỏng lực

Phần mềm mô phỏng lực đóng vai trò quan trọng trong việc giúp người dùng dễ dàng hình dung và phân tích các tác động của lực trong các bài toán cơ học. Một số phần mềm phổ biến bao gồm:

• ANSYS: Một trong những phần mềm mô phỏng cơ học mạnh mẽ nhất, được sử dụng để phân tích lực, nhiệt độ, và các yếu tố khác trong các hệ thống phức tạp.
• SolidWorks Simulation: Phần mềm này cung cấp các công cụ để mô phỏng và phân tích lực trong các mô hình 3D, giúp tối ưu hóa thiết kế sản phẩm.
• Autodesk Inventor: Với khả năng mô phỏng động học, Autodesk Inventor giúp người dùng tính toán và phân tích lực tác động lên các bộ phận máy móc.

5.2 Các công cụ tính toán lực trực tuyến

Các công cụ trực tuyến là giải pháp thuận tiện cho những ai cần tính toán lực một cách nhanh chóng mà không cần cài đặt phần mềm phức tạp. Một số công cụ đáng chú ý là:

• Force Calculator: Công cụ trực tuyến cho phép người dùng nhập các thông số như khối lượng, gia tốc để tính toán lực theo định luật của Newton.
• Vector Addition Calculator: Công cụ này hỗ trợ người dùng trong việc tổng hợp lực bằng cách tính toán tổng các vector lực dựa trên hướng và độ lớn của chúng.
• Online Physics Calculators: Một loạt các công cụ vật lý trực tuyến hỗ trợ tính toán lực, mô men, và các đại lượng khác liên quan đến tổng hợp lực.

Việc sử dụng các công cụ và phần mềm hỗ trợ không chỉ giúp tiết kiệm thời gian mà còn nâng cao độ chính xác trong các bài toán tổng hợp lực, đặc biệt trong các lĩnh vực như cơ khí, xây dựng và nghiên cứu khoa học.