Tổng Hợp 2 Lực Đồng Quy: Khái Niệm, Công Thức và Ứng Dụng Chi Tiết

Khi nghiên cứu về lực, một trong những khái niệm quan trọng là tổng hợp lực. Đặc biệt, trong trường hợp có hai lực đồng quy, việc xác định lực tổng hợp là một bài toán thường gặp trong vật lý. Dưới đây là các nội dung chi tiết về khái niệm và phương pháp tính tổng hợp 2 lực đồng quy.

1. Định Nghĩa Lực Đồng Quy

Hai lực đồng quy là hai lực có điểm đặt chung và tác dụng lên cùng một vật. Khi hai lực này được biểu diễn bằng các vectơ, chúng sẽ xuất phát từ một điểm gốc chung.

2. Quy Tắc Hình Bình Hành

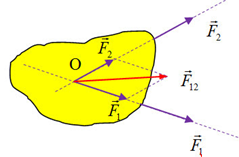
Để tổng hợp hai lực đồng quy, ta có thể sử dụng quy tắc hình bình hành. Theo quy tắc này, nếu hai lực \( \overrightarrow{F_1} \) và \( \overrightarrow{F_2} \) được biểu diễn bằng hai cạnh của một hình bình hành, thì đường chéo của hình bình hành chính là lực tổng hợp \( \overrightarrow{F_t} \).

Công thức tổng hợp hai lực đồng quy theo quy tắc hình bình hành được tính như sau:

\[
F_t = \sqrt{F_1^2 + F_2^2 + 2F_1F_2\cos\alpha}
\]
Trong đó:

• \( F_t \): Độ lớn của lực tổng hợp
• \( F_1, F_2 \): Độ lớn của hai lực thành phần
• \( \alpha \): Góc hợp bởi hai lực \( \overrightarrow{F_1} \) và \( \overrightarrow{F_2} \)

3. Phân Loại Các Trường Hợp

Trong quá trình tính toán, chúng ta có thể gặp các trường hợp đặc biệt như sau:

• Hai lực cùng phương, cùng chiều: Lực tổng hợp có độ lớn bằng tổng độ lớn của hai lực thành phần: \( F_t = F_1 + F_2 \).
• Hai lực cùng phương, ngược chiều: Lực tổng hợp có độ lớn bằng độ lớn chênh lệch giữa hai lực: \( F_t = |F_1 - F_2| \).
• Hai lực vuông góc nhau: Lực tổng hợp được tính theo định lý Pythagore: \( F_t = \sqrt{F_1^2 + F_2^2} \).

4. Bài Tập Minh Họa

Dưới đây là một số bài tập cơ bản để giúp bạn hiểu rõ hơn về khái niệm tổng hợp lực đồng quy:

5. Ứng Dụng Thực Tiễn

Quy tắc tổng hợp lực đồng quy không chỉ xuất hiện trong các bài toán vật lý mà còn được ứng dụng rộng rãi trong các lĩnh vực như xây dựng, cơ khí, và kỹ thuật để tính toán và thiết kế kết cấu chịu lực.

Việc nắm vững khái niệm và phương pháp tính toán tổng hợp lực đồng quy giúp ích rất nhiều trong việc giải quyết các bài toán liên quan đến lực trong cuộc sống hàng ngày cũng như trong các ngành kỹ thuật.

Lực đồng quy là các lực cùng tác dụng lên một vật tại một điểm và có khả năng tổng hợp thành một lực duy nhất. Trong thực tế, việc tổng hợp các lực đồng quy giúp xác định lực tổng hợp, tức là lực có thể thay thế các lực thành phần mà vẫn duy trì được tác động như ban đầu.

Giả sử chúng ta có hai lực đồng quy \(\vec{F}_1\) và \(\vec{F}_2\). Để tổng hợp hai lực này, ta sử dụng quy tắc hình bình hành:

• Bước 1: Vẽ hai vectơ lực \(\vec{F}_1\) và \(\vec{F}_2\) từ một điểm đồng quy.
• Bước 2: Từ đầu mút của mỗi vectơ, vẽ các đường song song với vectơ còn lại để tạo thành một hình bình hành.
• Bước 3: Đường chéo của hình bình hành chính là vectơ lực tổng hợp \(\vec{F}\).

Công thức tính lực tổng hợp theo quy tắc hình bình hành:

Trong đó:

• \(\vec{F}_1\) và \(\vec{F}_2\) là độ lớn của hai lực đồng quy.
• \(\theta\) là góc giữa hai lực \(\vec{F}_1\) và \(\vec{F}_2\).

Ví dụ: Nếu hai lực đồng quy có độ lớn lần lượt là 3 N và 4 N, và góc giữa chúng là 90°, lực tổng hợp sẽ là:

Như vậy, lực tổng hợp của hai lực đồng quy là một lực duy nhất có cùng hiệu quả như hai lực tác dụng đồng thời lên vật thể.

Quy tắc tổng hợp 2 lực đồng quy là phương pháp xác định lực tổng hợp từ hai lực tác dụng lên một điểm. Để tổng hợp hai lực đồng quy, chúng ta sử dụng quy tắc hình bình hành và quy tắc tam giác, là hai phương pháp cơ bản và phổ biến nhất.

2.1. Quy tắc hình bình hành

Quy tắc hình bình hành được áp dụng để xác định lực tổng hợp \(\vec{F}\) từ hai lực đồng quy \(\vec{F}_1\) và \(\vec{F}_2\) bằng cách dựng một hình bình hành với các cạnh tương ứng với hai vectơ lực.

• Bước 1: Vẽ hai vectơ lực \(\vec{F}_1\) và \(\vec{F}_2\) từ cùng một điểm xuất phát.
• Bước 2: Vẽ hai đường song song với các vectơ lực từ đầu mút của chúng để tạo thành một hình bình hành.
• Bước 3: Đường chéo của hình bình hành, xuất phát từ điểm chung của hai lực, chính là lực tổng hợp \(\vec{F}\).

Công thức tổng hợp hai lực theo quy tắc hình bình hành:

Trong đó:

• \(\vec{F}_1\) và \(\vec{F}_2\) là độ lớn của hai lực đồng quy.
• \(\theta\) là góc giữa hai lực \(\vec{F}_1\) và \(\vec{F}_2\).

2.2. Quy tắc tam giác

Quy tắc tam giác cũng là một phương pháp phổ biến để tổng hợp hai lực đồng quy. Theo quy tắc này, hai lực đồng quy được biểu diễn dưới dạng hai cạnh liên tiếp của một tam giác, và cạnh thứ ba của tam giác chính là lực tổng hợp.

• Bước 1: Vẽ vectơ lực \(\vec{F}_1\).
• Bước 2: Từ đầu mút của \(\vec{F}_1\), vẽ vectơ lực \(\vec{F}_2\).
• Bước 3: Vectơ từ điểm xuất phát của \(\vec{F}_1\) đến đầu mút của \(\vec{F}_2\) là lực tổng hợp \(\vec{F}\).

Ví dụ, nếu hai lực \(\vec{F}_1 = 5 \, \text{N}\) và \(\vec{F}_2 = 8 \, \text{N}\) tạo thành góc 60°, lực tổng hợp sẽ được tính bằng cách áp dụng công thức hình bình hành hoặc sử dụng quy tắc tam giác để xác định.

Để giải quyết các bài tập liên quan đến tổng hợp 2 lực đồng quy, chúng ta có thể áp dụng nhiều phương pháp khác nhau. Dưới đây là các bước cơ bản và các phương pháp phổ biến nhất:

3.1. Sử dụng quy tắc hình bình hành

Đây là phương pháp thường được sử dụng trong các bài tập liên quan đến tổng hợp lực đồng quy. Các bước thực hiện như sau:

1. Bước 1: Xác định độ lớn và phương của các lực \(\vec{F}_1\) và \(\vec{F}_2\).
2. Bước 2: Vẽ hai vectơ lực \(\vec{F}_1\) và \(\vec{F}_2\) từ cùng một điểm gốc.
3. Bước 3: Dựng hình bình hành bằng cách vẽ hai đường song song với các vectơ lực.
4. Bước 4: Xác định lực tổng hợp \(\vec{F}\) là đường chéo của hình bình hành xuất phát từ điểm gốc.
5. Bước 5: Tính toán độ lớn của lực tổng hợp bằng công thức: \[ \vec{F} = \sqrt{\vec{F}_1^2 + \vec{F}_2^2 + 2\vec{F}_1 \cdot \vec{F}_2 \cdot \cos(\theta)} \]

3.2. Sử dụng quy tắc tam giác

Phương pháp này cũng rất phổ biến và được sử dụng như sau:

1. Bước 1: Vẽ vectơ lực \(\vec{F}_1\) và \(\vec{F}_2\) sao cho chúng liên tiếp nhau, đầu mút của \(\vec{F}_1\) là điểm đầu của \(\vec{F}_2\).
2. Bước 2: Nối điểm xuất phát của \(\vec{F}_1\) với đầu mút của \(\vec{F}_2\), ta có được lực tổng hợp \(\vec{F}\).
3. Bước 3: Sử dụng các công thức lượng giác để tính toán độ lớn và phương của lực tổng hợp.

3.3. Sử dụng phương pháp thành phần

Đây là phương pháp phân tích các lực thành các thành phần vuông góc theo trục tọa độ, thường là trục \(Ox\) và \(Oy\):

1. Bước 1: Phân tích mỗi lực thành hai thành phần vuông góc.
2. Bước 2: Tính tổng các thành phần theo từng trục: \[ F_{x} = F_{1x} + F_{2x}, \quad F_{y} = F_{1y} + F_{2y} \]
3. Bước 3: Tìm độ lớn của lực tổng hợp: \[ \vec{F} = \sqrt{F_{x}^2 + F_{y}^2} \]
4. Bước 4: Tính góc hợp bởi lực tổng hợp với trục Ox: \[ \tan(\alpha) = \frac{F_y}{F_x} \]

Những phương pháp trên đều dựa trên cơ sở lý thuyết vật lý về vectơ lực và hình học, giúp giải quyết các bài toán một cách chính xác và hiệu quả.

Dưới đây là một số bài tập tiêu biểu về tổng hợp 2 lực đồng quy kèm theo lời giải chi tiết. Các bài tập này giúp củng cố kiến thức và rèn luyện kỹ năng tính toán trong các trường hợp khác nhau.

4.1. Bài tập 1

Đề bài: Hai lực đồng quy \(\vec{F}_1\) và \(\vec{F}_2\) có độ lớn lần lượt là 5 N và 12 N. Góc giữa hai lực là \(60^\circ\). Tính độ lớn của lực tổng hợp \(\vec{F}\).

Lời giải:

1. Bước 1: Sử dụng công thức tổng hợp lực: \[ \vec{F} = \sqrt{\vec{F}_1^2 + \vec{F}_2^2 + 2\vec{F}_1 \cdot \vec{F}_2 \cdot \cos(\theta)} \]
2. Bước 2: Thay số vào công thức: \[ \vec{F} = \sqrt{5^2 + 12^2 + 2 \cdot 5 \cdot 12 \cdot \cos(60^\circ)} = \sqrt{25 + 144 + 60} = \sqrt{229} \approx 15.13 \, \text{N} \]
3. Kết luận: Độ lớn của lực tổng hợp là \(15.13 \, \text{N}\).

4.2. Bài tập 2

Đề bài: Hai lực đồng quy \(\vec{F}_1\) và \(\vec{F}_2\) vuông góc với nhau, có độ lớn lần lượt là 8 N và 6 N. Tính độ lớn của lực tổng hợp \(\vec{F}\) và góc hợp bởi \(\vec{F}\) với \(\vec{F}_1\).

Lời giải:

1. Bước 1: Tính độ lớn của lực tổng hợp bằng định lý Pythagoras: \[ \vec{F} = \sqrt{\vec{F}_1^2 + \vec{F}_2^2} = \sqrt{8^2 + 6^2} = \sqrt{64 + 36} = \sqrt{100} = 10 \, \text{N} \]
2. Bước 2: Tính góc hợp bởi \(\vec{F}\) với \(\vec{F}_1\) bằng công thức: \[ \tan(\alpha) = \frac{F_2}{F_1} = \frac{6}{8} = 0.75 \] \[ \alpha = \arctan(0.75) \approx 36.87^\circ \]
3. Kết luận: Độ lớn của lực tổng hợp là \(10 \, \text{N}\), và góc hợp bởi lực tổng hợp với \(\vec{F}_1\) là \(36.87^\circ\).

4.3. Bài tập 3

Đề bài: Hai lực đồng quy có cùng độ lớn là 10 N. Tính độ lớn của lực tổng hợp khi góc giữa hai lực là \(120^\circ\).

Lời giải:

1. Bước 1: Áp dụng công thức tổng hợp lực: \[ \vec{F} = \sqrt{10^2 + 10^2 + 2 \cdot 10 \cdot 10 \cdot \cos(120^\circ)} \]
2. Bước 2: Thay số và tính toán: \[ \vec{F} = \sqrt{100 + 100 - 100} = \sqrt{100} = 10 \, \text{N} \]
3. Kết luận: Độ lớn của lực tổng hợp vẫn là \(10 \, \text{N}\) trong trường hợp này.

Việc nắm vững kiến thức về tổng hợp lực đồng quy đóng vai trò cực kỳ quan trọng trong cả học tập và ứng dụng thực tế. Đây là một phần kiến thức nền tảng trong vật lý, giúp học sinh hiểu rõ hơn về cách các lực tương tác và ảnh hưởng lẫn nhau.

• Nắm vững nguyên tắc cơ bản: Kiến thức về tổng hợp lực đồng quy giúp học sinh nắm vững các nguyên tắc cơ bản của động lực học, từ đó có thể áp dụng vào việc giải quyết các bài toán về lực một cách hiệu quả.
• Ứng dụng trong thực tiễn: Tổng hợp lực đồng quy không chỉ giới hạn trong các bài toán lý thuyết mà còn có nhiều ứng dụng trong cuộc sống thực, chẳng hạn như trong kỹ thuật xây dựng, cơ khí và các ngành khoa học kỹ thuật khác.
• Cải thiện kỹ năng giải bài tập: Hiểu rõ về cách tổng hợp lực giúp học sinh dễ dàng phân tích và giải quyết các bài toán về lực trong đề thi và bài tập. Đây cũng là một phần quan trọng trong chương trình vật lý phổ thông.
• Tư duy logic và sáng tạo: Việc học tập và hiểu biết về tổng hợp lực đồng quy giúp phát triển tư duy logic và sáng tạo, hỗ trợ học sinh trong việc học các môn khoa học khác cũng như trong cuộc sống hàng ngày.

Vì vậy, việc nắm vững kiến thức về tổng hợp lực đồng quy không chỉ giúp học sinh thành thạo trong môn vật lý mà còn là cơ sở để áp dụng vào nhiều lĩnh vực khác nhau, từ khoa học kỹ thuật đến đời sống thực tế.