Nguyên hàm căn x và tất tần tật thông tin về dạng toán căn x nguyên hàm chi tiết nhất

Giới thiệu

Bạn đã từng gặp phải bài toán về nguyên hàm căn x? Bạn đang muốn tìm hiểu về dạng toán này nhưng chưa biết bắt đầu từ đâu? Đừng lo, bài viết này sẽ cung cấp cho bạn tất cả những thông tin cần thiết về nguyên hàm căn x một cách chi tiết nhất. Hãy cùng tìm hiểu!

Nguyên hàm căn x là gì?

Theo định nghĩa của nguyên hàm, cho hàm số f(x) xác định trên K, hàm số F(x) được gọi là nguyên hàm của hàm số f(x) trên K nếu F'(x) = f(x) với mọi x ∈ K.

Bạn đang xem: Nguyên hàm căn x và tất tần tật thông tin về dạng toán căn x nguyên hàm chi tiết nhất

Với nguyên hàm căn x, phần biểu thức sẽ là những giá trị căn x, và chúng ta cần giải phương trình để tìm giá trị x.

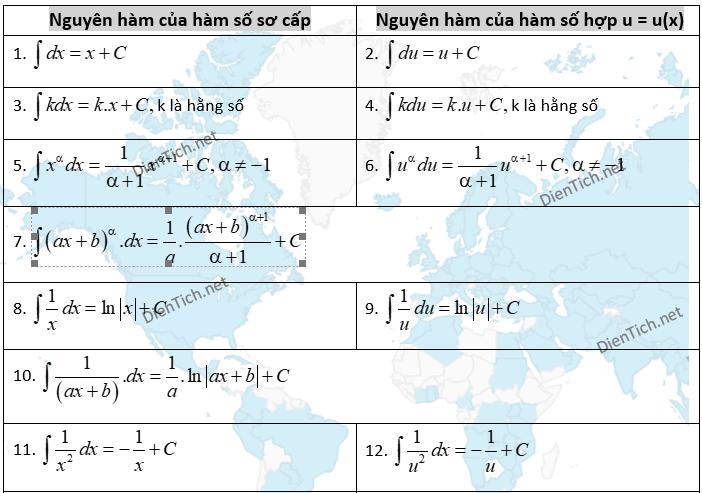
Công thức nguyên hàm của căn x chi tiết

Trong các dạng toán nguyên hàm, nguyên hàm của căn x là một dạng toán khó giải nhất. Dưới đây là một số công thức từ nguyên hàm căn bậc 2 của x đến nguyên hàm 1/căn x (cơ bản đến nâng cao) mà bạn sẽ gặp phải.

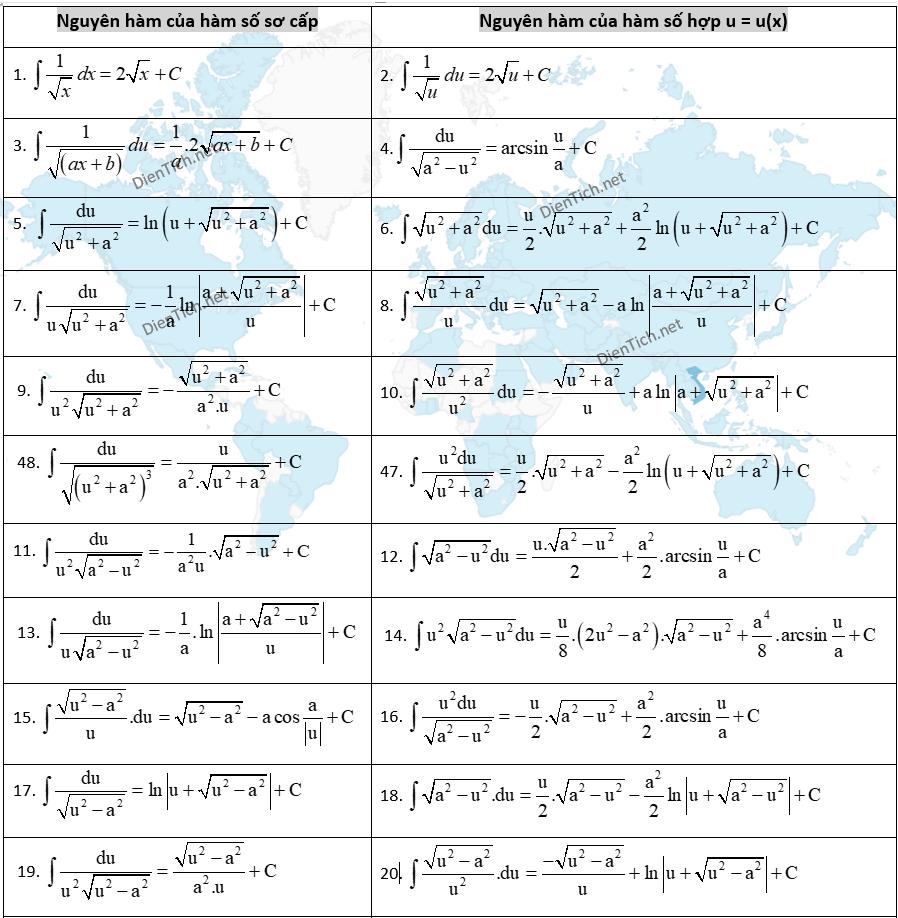
Các dạng bài tập về nguyên hàm căn x thường gặp và cách giải

Trong toán học, có một số dạng toán cơ bản mà chúng ta sử dụng công thức nguyên hàm căn x. Dưới đây là ví dụ và cách giải thể hiện chi tiết:

Tìm nguyên hàm của hàm chứa căn thức bằng phương pháp đổi biến số

Cách tìm nguyên hàm, tích phân bằng phương pháp đổi biến:

Cho hàm số u = u(x) có đạo hàm liên tục trên K và hàm số y = f(u) liên tục sao cho f[u(x)] xác định trên K. Khi đó nếu F là một nguyên hàm của f thì:

Ví dụ minh họa:

Nguyên hàm của hàm số là:

Lời giải:

Ta có:

Đặt u = 5x – 10 ta được:

Chọn B.

Tìm nguyên hàm các hàm số chứa căn thức (hàm số vô tỉ) dựa trên tam thức bậc hai

Trên cơ sở đưa tam thức bậc hai về dạng chính tắc và dùng các công thức sau:

Ví dụ 1: Tìm nguyên hàm các hàm số chứa căn x sau:

Tìm nguyên hàm của hàm số f(x)=x – ax + a, với a > 0

Ta có thể lựa chọn một trong hai cách sau:

Các nguyên hàm I1 và I2 chúng ta đã biết cách giải.

Tìm nguyên hàm của hàm số f(x)=dxax + b +ax + c

Khử tính vô tỉ ở mẫu số bằng cách trục căn thức, ta được:

Ví dụ: Tìm nguyên hàm của hàm số: f(x)=tan⁡x+12x+1+2x-1

Tìm nguyên hàm của hàm số chứa căn thức (hàm số vô tỉ) bằng cách sử dụng các đồng nhất thức.

Ví dụ: Tìm nguyên hàm của hàm số: f(x)=xx+110

Tìm nguyên hàm của hàm số: f(x)=v(x)dxu2x ±a

Ta thực hiện theo các bước sau:

Xem thêm : Cơ hội việc làm và mẫu CV Techcombank – hướng dẫn viết CV chuẩn

Sử dụng phương pháp hằng số bất định ta xác định được a, b, c

Bước 2: Áp dụng các công thức:

Ví dụ: Tìm nguyên hàm của hàm số f(x)=2×2+1×2+2x

Tìm nguyên hàm của hàm số: I=∫R(x,a2+x2).dx

Ta thực hiện theo các bước sau:

Tìm nguyên hàm của hàm số: I=∫R(x,x2-a2).dx

Ta thực hiện theo các bước sau:

Một số dạng bài tập nguyên hàm căn x tự luyện

Để giúp bạn nắm vững kiến thức và rèn luyện kỹ năng về nguyên hàm căn x, dưới đây là một số dạng bài tập mà bạn có thể tham khảo và thực hành:

Bài tập 1: Tính nguyên hàm của hàm số sau

Lời giải:

Bài tập 2: Tính nguyên hàm sau

Lời giải:

Bài tập 3: Tính

Lời giải

Bài tập 4: Tính nguyên hàm căn x của hàm số

Lời giải:

Bài tập 5 Tính

Lời giải

Kết luận

Trên đây là tổng hợp thông tin về dạng toán nguyên hàm căn x. Đây là một dạng toán khá khó, nên khi học thì cần nắm rõ công thức, các dạng toán và cách giải để có thể hoàn thành bài tập một cách chính xác nhất. Hy vọng rằng bài viết này đã giúp bạn hiểu rõ hơn về nguyên hàm căn x và cách giải quyết các bài tập liên quan. Chúc bạn thành công trong việc học tập và rèn luyện kỹ năng toán học!

Nguồn: https://ispacedanang.edu.vn
Danh mục: Học tập