Vào đầu học kì II của lớp 12, chúng ta sẽ bắt đầu học về nguyên hàm. Đây là một chương trình học mới, đòi hỏi chúng ta phải làm quen với những khái niệm và công thức nguyên hàm. Để giải nhanh và chính xác các bài tập về nguyên hàm, việc nhớ chính xác các công thức nguyên hàm là điều rất cần thiết. Bài viết này sẽ giúp bạn nắm vững các công thức nguyên hàm và cung cấp nhiều bài tập có lời giải chi tiết.
Contents
1. Bảng Công Thức Nguyên Hàm
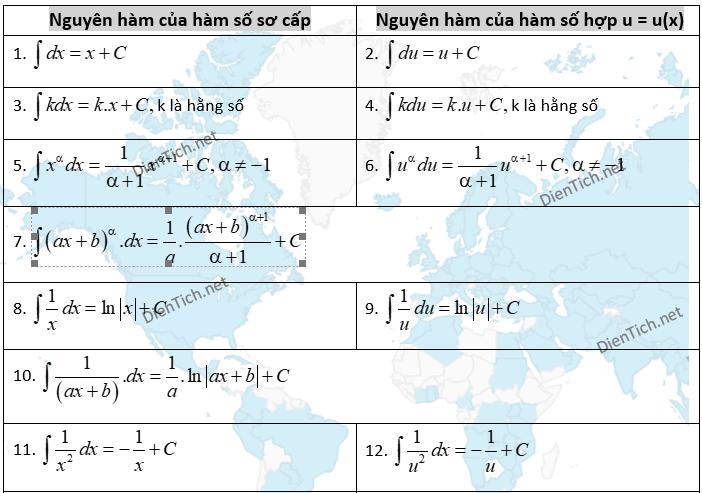
a) Công Thức Cơ Bản
Bảng công thức nguyên hàm cơ bản này gồm 12 công thức, sắp xếp như sau:
Bạn đang xem: LuyenThi
b) Nguyên Hàm Mũ
Trong phần này, chúng ta sẽ tìm hiểu về nguyên hàm của hàm mũ, được chia thành 8 công thức thuộc 2 chủ đề:
- Hàm mũ e
- Hàm mũ

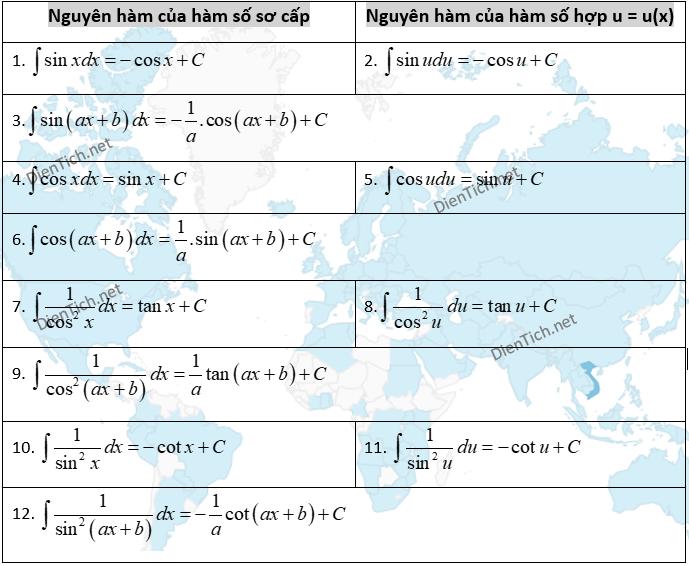
c) Nguyên Hàm Lượng Giác
Đây là bảng công thức nguyên hàm lượng giác, bao gồm 12 công thức thường xuyên gặp:
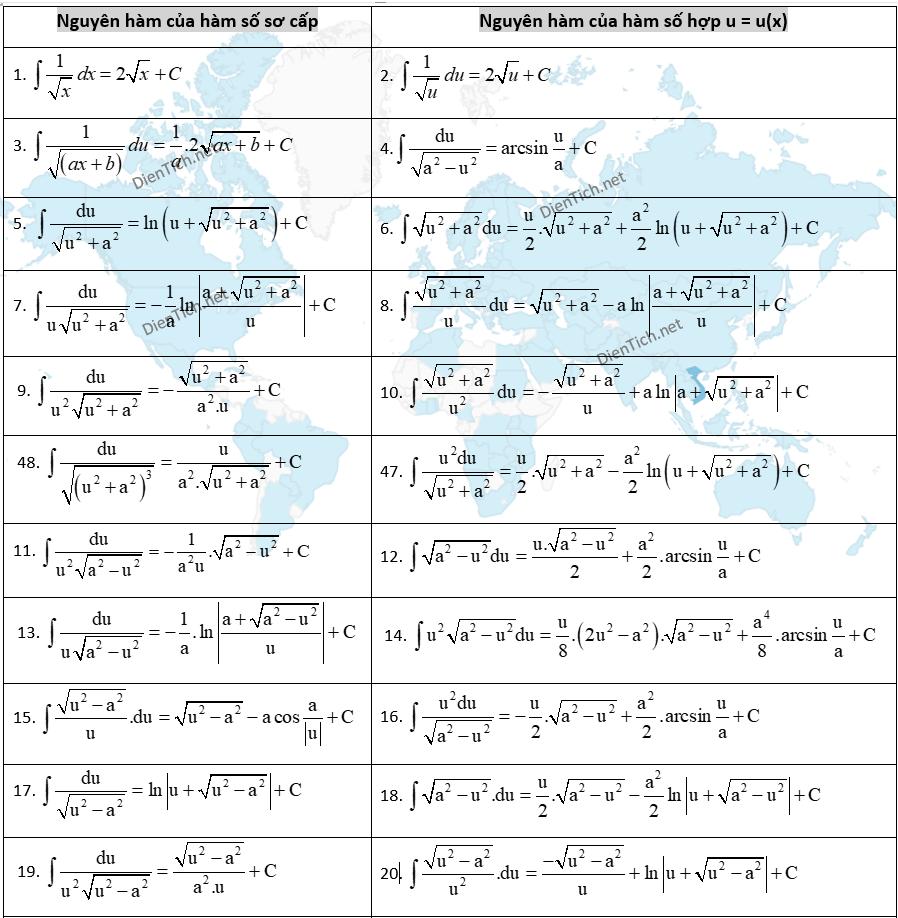
d) Công Thức Nguyên Hàm Căn Thức
Công thức nguyên hàm của căn thức cũng là một khái niệm khó khăn, nhưng trong bảng dưới đây, chúng tôi tuyển chọn những công thức thường gặp và sắp xếp từ căn bản tới nâng cao:
.png)
2. Bài Tập Nguyên Hàm
a) Bài Tập Có Lời Giải
Câu 1: Hãy tìm nguyên hàm của đa thức $int {frac{{ – {x^3} + 5x + 2}}{{4 – {x^2}}}dx} $.
- A. $frac{{{x^2}}}{2} – ln left| {2 – x} right| + C$.
- B. $frac{{{x^2}}}{2} + ln left| {2 – x} right| + C$.
- C. $frac{{{x^3}}}{3} – ln left| {2 – x} right| + C$.
- D. $frac{{{x^3}}}{3} + ln left| {x – 2} right| + C$.
Lời giải:
Chọn A
Vì $frac{{ – {x^3} + 5x + 2}}{{4 – {x^2}}}$$ = frac{{{x^3} – 5x – 2}}{{{x^2} – 4}}$$ = frac{{left( {x + 2} right)left( {{x^2} – 2x – 1} right)}}{{left( {x + 2} right)left( {x – 2} right)}}$$ = x – frac{1}{{x – 2}}$.
$ = int {left( {x – frac{1}{{x – 2}}} right){text{d}}x} = frac{{{x^2}}}{2} – ln left| {x – 2} right| + C$. $ Rightarrow int {frac{{ – {x^3} + 5x + 2}}{{4 – {x^2}}}{text{d}}x} $$ = int {left( {x – frac{1}{{x – 2}}} right){text{d}}x} $$ = frac{{{x^2}}}{2} – ln left| {x – 2} right| + C$
Câu 2: Tìm hàm số $f(x)$ biết rằng $f'(x) = ax + frac{b}{{{x^2}}}$ và thỏa mãn $f’left( 1 right) = 0;{text{ }}fleft( 1 right) = 4;{text{ }}fleft( { – 1} right) = 2$.
- A. $fleft( x right) = frac{{{x^2}}}{2} – frac{1}{x} – frac{5}{2}$.
- B. $fleft( x right) = frac{{{x^2}}}{2} + frac{1}{x} + frac{5}{2}$.
- C. $fleft( x right) = frac{{{x^2}}}{2} – frac{1}{x} + frac{5}{2}$.
- D. $fleft( x right) = frac{{{x^2}}}{2} + frac{1}{x} – frac{5}{2}$.
Lời giải:
Chọn B
Vì $f’left( 1 right) = 0 Rightarrow a + b = 0{text{ }}left( 1 right)$
Ta lại có $fleft( x right) = int {f’left( x right){text{d}}x} $$ = int {left( {ax + frac{b}{{{x^2}}}} right){text{d}}x} $$ = frac{{a{x^2}}}{2} – frac{b}{x} + C$
Vì $fleft( 1 right) = 4$$ Leftrightarrow frac{a}{2} – b + C = 4$$ Leftrightarrow a – 2b + 2C = 8{text{ }}left( 2 right)$
và $fleft( { – 1} right) = 2 Leftrightarrow frac{a}{2} + b + C = 2 Leftrightarrow a + 2b + 2C = 4{text{ }}left( 3 right)$
Giải hệ phương trình $left{ begin{array}{l} a + b = 0 a – 2b + 2C = 8 a + 2b + 2C = 4 end{array} right. Leftrightarrow left{ begin{array}{l} a = 1 b = – 1 c = frac{5}{2} end{array} right.$
Vậy $fleft( x right) = frac{{{x^2}}}{2} + frac{1}{x} + frac{5}{2}$
Câu 3: Giá trị $m,n$ để hàm số $Fleft( x right) = left( {2m + n} right){x^3} + left( {3m – 2n} right){x^2} – 4x$ là một nguyên hàm của hàm số $fleft( x right) = 3{x^2} + 10x – 4$. Khi đó $8m – 2n$ là:
- A. $6$.
- B. $12$.
- C. $10$.
- D. $ – 2$.
Lời giải:
Chọn C
$int {left( {3{x^2} + 10x – 4} right)dx = {x^3} + 5{x^2} – 4x + C} $
Khi đó ta có $left{ begin{array}{l} 2m + n = 1 3m – 2n = 5 C = 0 end{array} right. Leftrightarrow left{ begin{array}{l} m = 1 n = – 1 C = 0 end{array} right.$ nên $8m – 2n = 10$.
Câu 4: Tìm nguyên hàm của hàm số $f(x) = frac{{2{{sin }^3}x}}{{1 + cos x}}$.
- A. $int {f(x)dx = frac{1}{2}{{cos }^2}x – 2cos x + C} $.
- B. $int {f(x)dx = {{cos }^2}x – 2cos x + C} $.
- C. $int {f(x)dx = {{cos }^2}x + cos x} + C$.
- D. $int {f(x)dx = frac{1}{2}{{cos }^2}x + 2cos x + C} $.
Lời giải:
Chọn B
$int {left( {frac{{2{{sin }^3}x}}{{1 + cos x}}} right)dx} $ $ = int {left( {frac{{2sin x.{{sin }^2}x}}{{1 + cos x}}} right)dx} $ $ = int {left( {frac{{2sin xleft( {1 – {{cos }^2}x} right)}}{{1 + cos x}}} right)} dx$ $ = 2int {sin xleft( {1 – cos x} right)dx} $ $ = int {2left( {cos x – 1} right)dleft( {cos x} right)} $$ = {cos ^2}x – 2cos x + C$
Câu 5: Tìm nguyên hàm của hàm số $f(x) = frac{{{{cos }^3}x}}{{{{sin }^5}x}}$.
- A. $int {f(x).dx = } frac{{ – {{cot }^4}x}}{4} + C$.
- B. $int {f(x).dx = } frac{{{{cot }^4}x}}{4} + C$.
- C. $int {f(x).dx = } frac{{{{cot }^2}x}}{2} + C$.
- D. $int {f(x).dx = } frac{{{{tan }^4}x}}{4} + C$.
Xem thêm : Tự đánh giá bản thân trong báo cáo thử việc [2024]
Lời giải:
Chọn A
$int {frac{{{{cos }^3}xdx}}{{{{sin }^5}x}}} $ $ = int {{{cot }^3}x.frac{{dx}}{{{{sin }^2}x}}} $ $ = – int {{{cot }^3}x.dleft( {cot x} right)} $ $ = frac{{ – {{cot }^4}x}}{4} + C$
Câu 6: Tìm nguyên hàm của hàm số $f(x) = cos 2xleft( {{{sin }^4}x + {{cos }^4}x} right)$.
- A. $int {f(x).dx = } sin 2x – frac{1}{4}{sin ^3}2x + C$
- B. $int {f(x).dx = } frac{1}{2}sin 2x + frac{1}{{12}}{sin ^3}2x + C$.
- C. $int {f(x).dx = } frac{1}{2}sin 2x – frac{1}{{12}}{sin ^3}2x + C$.
- D. $int {f(x).dx = } frac{1}{2}sin 2x – frac{1}{4}{sin ^3}2x + C$.
Lời giải:
Chọn C
$int {cos 2xleft( {{{sin }^4}x + {{cos }^4}x} right)dx} $ $ = int {cos 2xleft[ {left( {{{sin }^2}x + {{cos }^2}x} right) – 2{{sin }^2}x.{{cos }^2}x} right]dx$ $ = int {cos 2xleft( {1 – frac{1}{2}{{sin }^2}2x} right)dx} $ $ = int {cos 2xdx} – frac{1}{2}int {{{sin }^2}2x.cos 2xdx} $ $ = frac{1}{2}sin 2x – frac{1}{{12}}{sin ^3}2x + C$
Câu 7: Tìm nguyên hàm của hàm số $f(x) = left( {tan x + {e^{2sin x}}} right)cos x$.
- A. $int {f(x)dx = } – cos x + frac{1}{2}{e^{2sin x}} + C$.
- B. $int {f(x)dx = } cos x + frac{1}{2}{e^{2sin x}} + C$.
- C. $int {f(x)dx = } – cos x + {e^{2sin x}} + C$.
- D. $int {f(x)dx = } – cos x – frac{1}{2}{e^{2sin x}} + C$.
Lời giải:
Chọn A
$int {left( {tan x + {e^{2sin x}}} right)cos xdx} $ $ = int {sin xdx} + int {{e^{2sin x}}dleft( {sin x} right)} $ $ = – cos x + frac{1}{2}{e^{2sin x}} + C$
b) Bài Tập Trắc Nghiệm Nguyên Hàm Tự Luyện
Câu 1: Nguyên hàm của hàm số $fleft( x right) = 2{x^3} – 9.$
- A. $frac{1}{2}{x^4} – 9x + C.$
- B. $4{x^4} – 9x + C.$
- C. $frac{1}{4}{x^4} + C.$
- D. $4{x^3} + 9x + C.$
Câu 2: Nguyên hàm của hàm số $fleft( x right) = {x^2} – frac{5}{x} + frac{3}{{{x^2}}} – frac{1}{3}$.
- A. $frac{{{x^3}}}{3} – 5ln left| x right| – frac{3}{x} – frac{1}{3}x + C$
- B. $frac{{{x^3}}}{3} – 5ln left| x right| + frac{3}{x} – frac{1}{3}x + C$
- C. $2{x^3} – 5ln left| x right| – frac{3}{x} – frac{1}{3}x + C$
- D. $2x – frac{5}{{{x^2}}} + frac{{3x}}{{{x^4}}} + C$
Câu 3: Nguyên hàm của hàm số $fleft( x right) = frac{1}{{{x^2}}} – {x^2} – frac{1}{3}$ là:
- A. $ – frac{{{x^4} + {x^2} + 3}}{{3x}} + C$
- B. $ – frac{{{x^3}}}{3} + frac{1}{x} – frac{x}{3} + C$
- C. $frac{{ – {x^4} + {x^2} + 3}}{{3x}} + C$
- D. $ – frac{1}{x} – frac{{{x^3}}}{3} + C$
Câu 4: Nguyên hàm của hàm số $fleft( x right) = sqrt[3]{x}$
- A. $Fleft( x right) = frac{{3sqrt[3]{{{x^2}}}}}{4} + C$
- B. $Fleft( x right) = frac{{3xsqrt[3]{x}}}{4} + C$
- C. $Fleft( x right) = frac{{4x}}{{3sqrt[3]{x}}} + C$
- D. $Fleft( x right) = frac{{4x}}{{3sqrt[3]{{{x^2}}}}} + C$
Câu 5: Nguyên hàm của hàm số $fleft( x right) = frac{1}{{xsqrt x }}$
- A. $Fleft( x right) = frac{2}{{sqrt x }} + C$
- B. $Fleft( x right) = – frac{2}{{sqrt x }} + C$
- C. $Fleft( x right) = frac{{sqrt x }}{2} + C$
- D. $Fleft( x right) = – frac{{sqrt x }}{2} + C$
Trên đây là các công thức nguyên hàm lớp 12 từ cơ bản tới nâng cao. Để làm tốt các bài tập và rút gọn biểu thức, việc nhớ chính xác các công thức trong bảng trên là rất quan trọng. Hãy luyện tập và áp dụng công thức một cách thành thạo để giải các bài tập nhanh chóng và chính xác. Nguyên hàm là một chủ đề mới, có nhiều công thức và bài tập phức tạp, nhưng nếu bạn chăm chỉ học và thường xuyên xem lại bài viết này cùng với việc luyện tập, nó sẽ trở nên đơn giản hơn nhiều.
Nguồn: https://ispacedanang.edu.vn
Danh mục: Học tập