Chủ đề trong chuyển động thẳng biến đổi đều hệ số góc: Trong chuyển động thẳng biến đổi đều, hệ số góc đóng vai trò quan trọng trong việc xác định sự thay đổi vận tốc và gia tốc của vật. Bài viết này sẽ giúp bạn hiểu rõ khái niệm này và cách áp dụng vào các bài toán thực tiễn cũng như trong đời sống hàng ngày, từ lý thuyết đến thực hành.
Mục lục
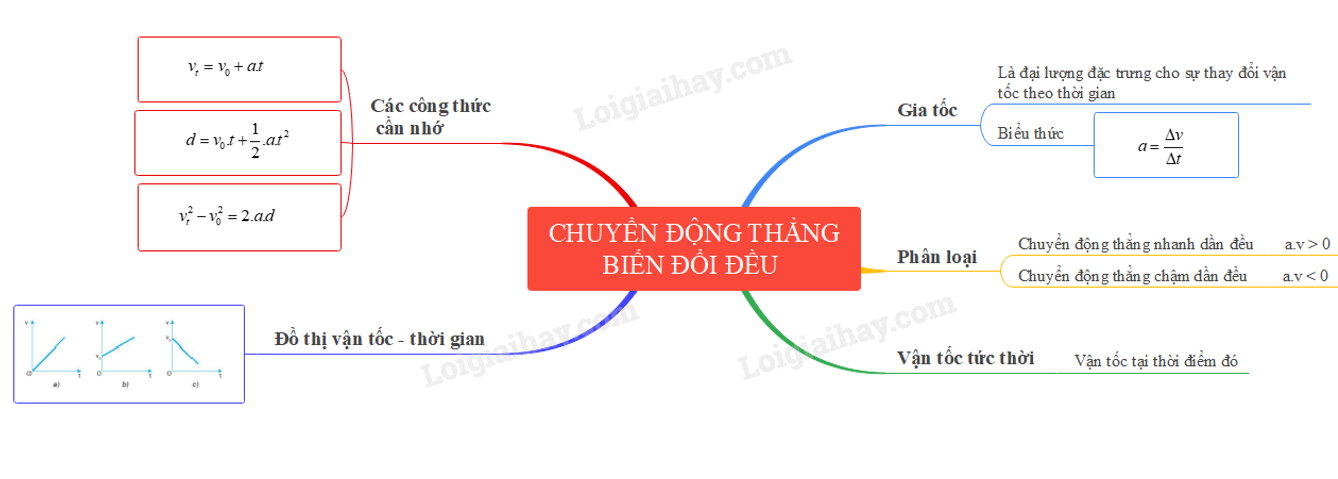
Chuyển Động Thẳng Biến Đổi Đều và Hệ Số Góc
Trong chuyển động thẳng biến đổi đều, hệ số góc của đường biểu diễn vận tốc theo thời gian là yếu tố quyết định đến gia tốc của vật. Hệ số góc càng lớn thì gia tốc càng lớn, và ngược lại.
1. Hệ số góc của đồ thị vận tốc - thời gian
Đồ thị vận tốc - thời gian \( v(t) \) trong chuyển động thẳng biến đổi đều thường là một đường thẳng. Hệ số góc của đường này tương ứng với gia tốc \( a \) của vật.
- Nếu đường thẳng có hệ số góc dương \( a > 0 \), vật đang chuyển động nhanh dần đều.
- Nếu đường thẳng có hệ số góc âm \( a < 0 \), vật đang chuyển động chậm dần đều.
2. Công thức liên quan đến hệ số góc và gia tốc
- Gia tốc \( a \) trong chuyển động thẳng biến đổi đều được tính theo công thức:
\[
a = \frac{\Delta v}{\Delta t}
\]
trong đó:
- \( \Delta v \): sự thay đổi của vận tốc
- \( \Delta t \): khoảng thời gian thay đổi
- Phương trình vận tốc theo thời gian:
\[
v(t) = v_0 + at
\]
trong đó:
- \( v_0 \): vận tốc ban đầu
- \( a \): gia tốc
- \( t \): thời gian
3. Đồ thị trong chuyển động thẳng biến đổi đều
Đồ thị vận tốc - thời gian có thể chia thành hai loại:
- Chuyển động nhanh dần đều: Đường thẳng \( v(t) \) dốc lên, tương ứng với \( a > 0 \).
- Chuyển động chậm dần đều: Đường thẳng \( v(t) \) dốc xuống, tương ứng với \( a < 0 \).
4. Ví dụ về bài toán chuyển động thẳng biến đổi đều
Giả sử một vật chuyển động với vận tốc ban đầu \( v_0 = 0 \) và gia tốc \( a = 2 \, \text{m/s}^2 \). Sau \( 5 \, \text{giây} \), vận tốc của vật là bao nhiêu?
- Áp dụng phương trình vận tốc: \[ v(t) = v_0 + at = 0 + 2 \cdot 5 = 10 \, \text{m/s} \]
5. Kết luận
Trong chuyển động thẳng biến đổi đều, hệ số góc của đường biểu diễn vận tốc theo thời gian là một công cụ mạnh mẽ giúp chúng ta hiểu và dự đoán các đặc tính chuyển động của vật. Việc nắm rõ hệ số góc giúp phân tích chính xác các bài toán về gia tốc và vận tốc trong vật lý.

.png)
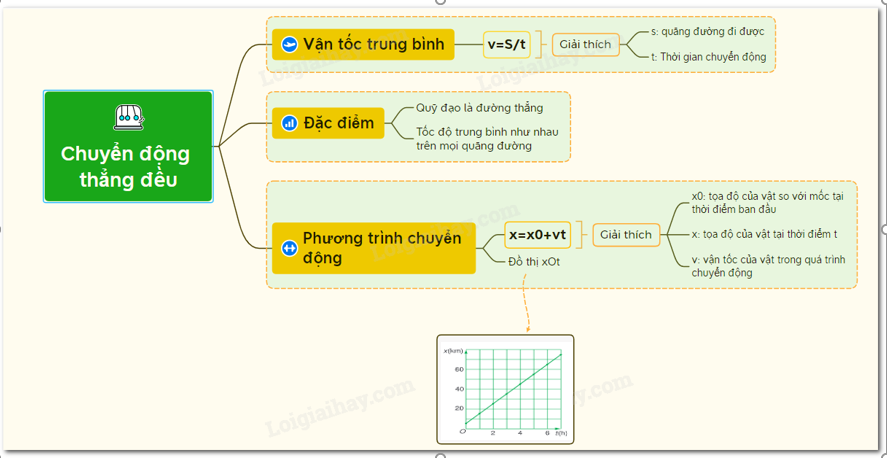
1. Khái Niệm Chuyển Động Thẳng Biến Đổi Đều
Chuyển động thẳng biến đổi đều là dạng chuyển động mà vận tốc của vật thay đổi đều theo thời gian. Đặc điểm nổi bật của chuyển động này là quỹ đạo của vật là đường thẳng, và độ lớn vận tốc thay đổi tuyến tính theo thời gian.
- Trong chuyển động thẳng nhanh dần đều, vận tốc của vật tăng dần theo thời gian.
- Trong chuyển động thẳng chậm dần đều, vận tốc của vật giảm dần theo thời gian.
Phương trình chuyển động thẳng biến đổi đều được xác định theo công thức:
Trong đó:
- \(x\): Tọa độ của vật sau thời gian \(t\).
- \(x_0\): Tọa độ ban đầu của vật.
- \(v_0\): Vận tốc ban đầu của vật.
- \(a\): Gia tốc của vật.
- \(t\): Thời gian chuyển động.
Hệ số góc của đường thẳng biểu diễn chuyển động thẳng biến đổi đều là gia tốc \(a\), đóng vai trò quyết định sự thay đổi của vận tốc trong quá trình chuyển động.
2. Công Thức Tính Vận Tốc Trong Chuyển Động Thẳng Biến Đổi Đều
Trong chuyển động thẳng biến đổi đều, vận tốc của vật thay đổi theo thời gian và có thể tính toán thông qua công thức sau:
Trong đó:
- \(v\): Vận tốc của vật sau thời gian \(t\).
- \(v_0\): Vận tốc ban đầu của vật.
- \(a\): Gia tốc của vật (có thể dương hoặc âm, tùy thuộc vào việc chuyển động nhanh dần hay chậm dần).
- \(t\): Thời gian chuyển động.
Vận tốc tức thời tại bất kỳ thời điểm nào có thể tính dựa trên hệ số góc của đồ thị vận tốc - thời gian. Nếu hệ số góc là dương, vật chuyển động nhanh dần đều; nếu hệ số góc là âm, vật chuyển động chậm dần đều.
Công thức này giúp ta dễ dàng xác định vận tốc tức thời của vật và áp dụng vào các bài toán thực tế.

3. Ứng Dụng Thực Tiễn
Chuyển động thẳng biến đổi đều và hệ số góc có nhiều ứng dụng quan trọng trong đời sống và khoa học kỹ thuật. Dưới đây là một số ứng dụng thực tiễn:
- Giao thông vận tải: Công thức và khái niệm về vận tốc và gia tốc được sử dụng để thiết kế các hệ thống phanh xe, đảm bảo an toàn khi di chuyển trên đường.
- Vũ trụ học: Chuyển động của tên lửa và vệ tinh trong không gian được mô phỏng dựa trên nguyên lý của chuyển động thẳng biến đổi đều, giúp tính toán quỹ đạo và vận tốc cần thiết.
- Thể thao: Trong các môn thể thao như đua xe, điền kinh, vận động viên cần điều chỉnh vận tốc và gia tốc để đạt hiệu suất tối ưu, ứng dụng công thức của chuyển động thẳng biến đổi đều.
- Kỹ thuật: Trong lĩnh vực kỹ thuật, đặc biệt là ngành cơ khí, chuyển động thẳng biến đổi đều được sử dụng để phân tích và thiết kế máy móc, đặc biệt là hệ thống truyền động và robot.
Ứng dụng của chuyển động thẳng biến đổi đều không chỉ giúp giải quyết các vấn đề trong nghiên cứu khoa học mà còn đóng vai trò quan trọng trong việc nâng cao chất lượng cuộc sống hàng ngày.

4. Các Công Thức Toán Học Liên Quan
Trong chuyển động thẳng biến đổi đều, các công thức toán học liên quan thường được sử dụng để tính toán vận tốc, gia tốc và quãng đường di chuyển. Dưới đây là một số công thức quan trọng:
- Công thức tính vận tốc tức thời:
\[
v = v_0 + a \cdot t
\]
Trong đó:
- \(v\): vận tốc tức thời (m/s)
- \(v_0\): vận tốc ban đầu (m/s)
- \(a\): gia tốc (m/s²)
- \(t\): thời gian chuyển động (s)
- Công thức tính quãng đường:
\[
s = v_0 \cdot t + \frac{1}{2}a \cdot t^2
\]
Trong đó:
- \(s\): quãng đường di chuyển (m)
- \(v_0\): vận tốc ban đầu (m/s)
- \(a\): gia tốc (m/s²)
- \(t\): thời gian chuyển động (s)
- Công thức liên hệ giữa vận tốc, gia tốc và quãng đường:
\[
v^2 = v_0^2 + 2a \cdot s
\]
Trong đó:
- \(v\): vận tốc tức thời (m/s)
- \(v_0\): vận tốc ban đầu (m/s)
- \(a\): gia tốc (m/s²)
- \(s\): quãng đường di chuyển (m)
Các công thức này là nền tảng quan trọng để phân tích chuyển động trong nhiều bài toán vật lý và ứng dụng thực tiễn trong đời sống.

5. Mở Rộng Kiến Thức
Chuyển động thẳng biến đổi đều không chỉ giới hạn trong những bài toán vật lý cơ bản mà còn có ứng dụng rộng rãi trong nhiều lĩnh vực khác nhau. Dưới đây là một số kiến thức mở rộng giúp bạn hiểu sâu hơn về khái niệm này:
- Chuyển động tròn đều:
Mặc dù có vẻ khác biệt, nhưng chuyển động tròn đều có thể được phân tích bằng cách sử dụng các nguyên tắc tương tự như chuyển động thẳng biến đổi đều, đặc biệt là khi tính gia tốc hướng tâm.
- Chuyển động trong môi trường có lực cản:
Khi có lực cản như lực ma sát hoặc lực cản của không khí, chuyển động thẳng biến đổi đều sẽ chịu ảnh hưởng, dẫn đến việc tính toán thêm lực và momen lực.
- Phương pháp thực nghiệm:
Nghiên cứu chuyển động thực tế qua các bài thí nghiệm như sử dụng máy quay chậm và phần mềm phân tích chuyển động giúp củng cố lý thuyết đã học.
Những kiến thức mở rộng này không chỉ giúp học sinh nắm chắc nền tảng lý thuyết mà còn ứng dụng vào thực tiễn, từ đó phát triển tư duy sáng tạo trong học tập và nghiên cứu.