Số Vân Giao Thoa Cực Đại: Tìm Hiểu Chi Tiết và Ứng Dụng Thực Tế

Hiện tượng giao thoa sóng là một trong những hiện tượng vật lý quan trọng, đặc biệt là trong nghiên cứu sóng cơ và sóng ánh sáng. Trong đó, khái niệm "số vân giao thoa cực đại" là một yếu tố then chốt để hiểu rõ hơn về sự phân bố các điểm có biên độ lớn nhất trên mặt sóng.

1. Khái Niệm Số Vân Giao Thoa Cực Đại

Số vân giao thoa cực đại được xác định là số lượng các đường cực đại (vân sáng) xuất hiện trong một hiện tượng giao thoa. Các vân cực đại là những vị trí trên mặt sóng nơi biên độ dao động của sóng đạt giá trị lớn nhất, xảy ra khi hai sóng gặp nhau và cùng pha.

2. Công Thức Xác Định Số Vân Giao Thoa Cực Đại

Số vân giao thoa cực đại có thể được tính toán bằng công thức:

\[
N_{\text{max}} = 2\left\lfloor \frac{l}{\lambda} \right\rfloor + 1
\]

Trong đó:

• \(N_{\text{max}}\): Số vân giao thoa cực đại.
• \(l\): Khoảng cách giữa hai nguồn sóng.
• \(\lambda\): Bước sóng của sóng.
• \(\left\lfloor x \right\rfloor\): Hàm lấy phần nguyên của x.

3. Ứng Dụng và Ví Dụ

Hiện tượng giao thoa và số vân giao thoa cực đại có nhiều ứng dụng trong thực tiễn, đặc biệt là trong các thí nghiệm vật lý và công nghệ quang học. Ví dụ:

• Trong thí nghiệm Young về giao thoa ánh sáng, số vân cực đại giúp xác định bước sóng ánh sáng.
• Trong kỹ thuật laser, số vân giao thoa được sử dụng để kiểm soát và điều chỉnh các chùm sóng.

4. Ví Dụ Cụ Thể

Giả sử trong một thí nghiệm giao thoa trên mặt nước với hai nguồn sóng kết hợp cách nhau 12,5 cm, dao động cùng pha với tần số 10 Hz, và tốc độ truyền sóng trên mặt nước là 20 cm/s, số vân giao thoa cực đại có thể được tính như sau:

\[
\lambda = \frac{v}{f} = \frac{20 \, \text{cm/s}}{10 \, \text{Hz}} = 2 \, \text{cm}
\]

Do đó, số vân giao thoa cực đại là:

\[
N_{\text{max}} = 2\left\lfloor \frac{12,5 \, \text{cm}}{2 \, \text{cm}} \right\rfloor + 1 = 2\left\lfloor 6,25 \right\rfloor + 1 = 13
\]

5. Kết Luận

Việc hiểu và áp dụng số vân giao thoa cực đại không chỉ giúp trong việc giải các bài toán vật lý mà còn đóng vai trò quan trọng trong nhiều lĩnh vực khoa học và công nghệ.

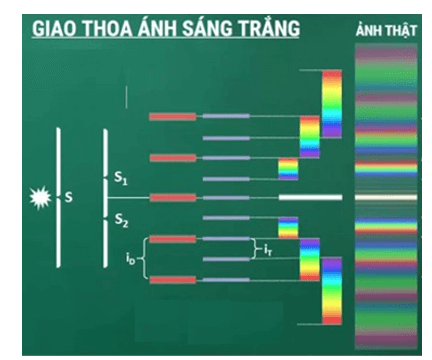
Hiện tượng giao thoa sóng là một hiện tượng vật lý quan trọng, xuất hiện khi hai hay nhiều sóng gặp nhau và tác động qua lại. Giao thoa sóng có thể xảy ra trong nhiều môi trường khác nhau như trên mặt nước, trong không khí, hay trong các môi trường rắn.

Trong hiện tượng giao thoa, các sóng có thể giao thoa với nhau tạo thành các vùng tăng cường (cực đại) hoặc triệt tiêu (cực tiểu). Những điểm có biên độ dao động lớn nhất được gọi là các "vân giao thoa cực đại". Đây là những điểm mà hai sóng đến cùng pha và tổng hợp biên độ của chúng để tạo ra dao động mạnh nhất.

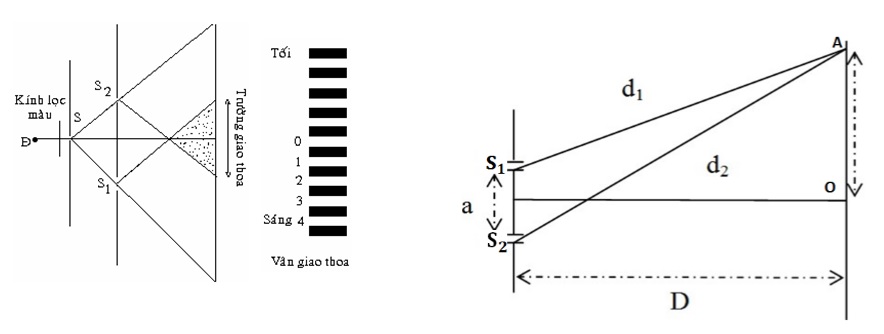
Để dễ hiểu hơn, khi hai nguồn sóng phát ra cùng tần số và dao động cùng pha, chúng sẽ tạo ra các vùng giao thoa. Nếu chúng ta xét một điểm trên mặt sóng, tại điểm này, nếu khoảng cách từ nó đến hai nguồn sóng chênh lệch một số nguyên lần bước sóng \(\lambda\), thì tại đó sẽ xuất hiện vân giao thoa cực đại.

• Điều kiện xuất hiện vân cực đại: Điểm M nằm trên vân cực đại khi thỏa mãn điều kiện: \[ d_2 - d_1 = k\lambda \] với \(k\) là số nguyên, \(d_1\) và \(d_2\) là khoảng cách từ điểm M đến hai nguồn sóng, \(\lambda\) là bước sóng.

Các vân cực đại thường được sử dụng trong các thí nghiệm và ứng dụng thực tế như xác định bước sóng của ánh sáng trong thí nghiệm Young, phân tích cấu trúc vật chất, hay trong các hệ thống quang học tiên tiến.

Số vân giao thoa cực đại là số lượng các điểm trên mặt phẳng sóng mà tại đó biên độ dao động đạt giá trị lớn nhất. Để tính số vân giao thoa cực đại, ta sử dụng các công thức phụ thuộc vào bước sóng, khoảng cách giữa hai nguồn sóng, và điều kiện giao thoa.

Công thức cơ bản để xác định số vân giao thoa cực đại \(N_{\text{max}}\) trong hiện tượng giao thoa sóng cơ là:

\[
N_{\text{max}} = 2\left\lfloor \frac{l}{\lambda} \right\rfloor + 1
\]

Trong đó:

• \(l\): Khoảng cách giữa hai nguồn sóng.
• \(\lambda\): Bước sóng của sóng.
• \(\left\lfloor x \right\rfloor\): Ký hiệu của hàm lấy phần nguyên, nghĩa là lấy giá trị nguyên lớn nhất không vượt quá x.

Quá trình tính toán số vân giao thoa cực đại thực hiện như sau:

1. Xác định khoảng cách giữa hai nguồn sóng \(l\).
2. Tính bước sóng \(\lambda\) dựa trên các thông số có sẵn như tốc độ truyền sóng \(v\) và tần số sóng \(f\) theo công thức: \(\lambda = \frac{v}{f}\).
3. Áp dụng công thức trên để tính \(N_{\text{max}}\), từ đó xác định số lượng vân cực đại xuất hiện.

Ví dụ, nếu hai nguồn sóng cách nhau \(l = 12,5 \, \text{cm}\) và bước sóng \(\lambda = 2 \, \text{cm}\), số vân giao thoa cực đại sẽ được tính như sau:

\[
N_{\text{max}} = 2\left\lfloor \frac{12,5 \, \text{cm}}{2 \, \text{cm}} \right\rfloor + 1 = 2 \times 6 + 1 = 13
\]

Như vậy, có 13 vân giao thoa cực đại sẽ xuất hiện trong thí nghiệm này.

Hiện tượng giao thoa sóng không chỉ là một khái niệm lý thuyết trong vật lý mà còn có nhiều ứng dụng quan trọng trong các lĩnh vực khác nhau của khoa học và công nghệ. Dưới đây là một số ứng dụng tiêu biểu của hiện tượng giao thoa sóng:

• Trong Quang Học: Giao thoa ánh sáng là một phương pháp quan trọng trong việc đo lường bước sóng ánh sáng. Thí nghiệm Young về giao thoa ánh sáng là một ứng dụng kinh điển, giúp xác định tính chất sóng của ánh sáng. Công nghệ quang học sử dụng hiện tượng này để phát triển các thiết bị như máy đo giao thoa (interferometer), được sử dụng trong việc đo lường chính xác các khoảng cách rất nhỏ, kiểm tra chất lượng bề mặt quang học và phân tích cấu trúc của các vật liệu.
• Trong Âm Học: Hiện tượng giao thoa âm thanh được sử dụng để tạo ra các vùng âm thanh có cường độ khác nhau, từ đó ứng dụng trong việc thiết kế phòng thu âm, phòng hòa nhạc, và các hệ thống âm thanh. Nhờ hiện tượng này, kỹ thuật xử lý âm thanh có thể loại bỏ hoặc giảm thiểu tiếng ồn không mong muốn, đồng thời tăng cường chất lượng âm thanh trong các môi trường khác nhau.
• Trong Công Nghệ Laser: Giao thoa sóng cũng đóng vai trò quan trọng trong công nghệ laser, đặc biệt là trong các ứng dụng liên quan đến đo lường và khắc chính xác. Laser giao thoa (holography) sử dụng nguyên lý giao thoa sóng để tạo ra các hình ảnh ba chiều với độ chính xác cao. Điều này được ứng dụng trong nhiều lĩnh vực như y học, kỹ thuật, và nghệ thuật.
• Trong Kỹ Thuật Vô Tuyến: Trong lĩnh vực truyền thông vô tuyến, hiện tượng giao thoa sóng vô tuyến được sử dụng để cải thiện chất lượng tín hiệu, tối ưu hóa băng thông và giảm nhiễu. Các kỹ thuật như MIMO (Multiple Input Multiple Output) dựa trên nguyên lý giao thoa để tăng cường khả năng truyền dẫn trong các mạng không dây.
• Trong Nghiên Cứu Khoa Học: Hiện tượng giao thoa sóng còn được sử dụng trong nghiên cứu các tính chất của vật liệu, xác định cấu trúc tinh thể và phân tích phổ. Đây là một công cụ quan trọng trong các thí nghiệm vật lý, đặc biệt là trong các nghiên cứu về vật liệu nano và các dạng vật chất mới.

Nhờ các ứng dụng đa dạng của hiện tượng giao thoa sóng, khoa học và công nghệ đã đạt được nhiều tiến bộ đáng kể, từ việc nâng cao chất lượng cuộc sống đến phát triển các công nghệ mới mang tính đột phá.

Để hiểu rõ hơn về số vân giao thoa cực đại và hiện tượng giao thoa sóng, việc thực hiện thí nghiệm và giải bài tập minh họa là rất quan trọng. Dưới đây là một ví dụ thí nghiệm cơ bản và một số bài tập minh họa chi tiết:

4.1 Thí Nghiệm Young về Giao Thoa Ánh Sáng

Thí nghiệm Young là một thí nghiệm kinh điển để quan sát hiện tượng giao thoa ánh sáng. Thí nghiệm này sử dụng hai khe hẹp song song với nhau, qua đó ánh sáng từ một nguồn đơn sắc đi qua và tạo ra các vân giao thoa trên màn.

Quá trình thực hiện:

1. Chuẩn bị một nguồn sáng đơn sắc (ví dụ: đèn laser), hai khe hẹp song song (khoảng cách giữa hai khe là \(d\)), và một màn chiếu để quan sát các vân giao thoa.
2. Chiếu ánh sáng từ nguồn qua hai khe hẹp. Khi ánh sáng đi qua hai khe, nó sẽ bị nhiễu xạ và giao thoa với nhau, tạo ra các vân sáng và tối trên màn chiếu.
3. Quan sát và đo khoảng cách giữa các vân sáng (hoặc tối) liên tiếp, từ đó có thể tính được bước sóng của ánh sáng dựa trên công thức: \[ y = \frac{\lambda L}{d} \] trong đó \(y\) là khoảng cách giữa hai vân sáng (hoặc tối) liên tiếp, \(L\) là khoảng cách từ khe đến màn, và \(\lambda\) là bước sóng ánh sáng.

4.2 Bài Tập Minh Họa

Dưới đây là một bài tập minh họa để tính số vân giao thoa cực đại:

• Bài Tập: Hai nguồn sóng cùng pha, cách nhau một khoảng \(d = 10 \, \text{cm}\). Sóng có bước sóng \(\lambda = 2 \, \text{cm}\). Hãy tính số vân giao thoa cực đại xuất hiện trên mặt phẳng chứa hai nguồn sóng.
• Lời Giải: Sử dụng công thức: \[ N_{\text{max}} = 2\left\lfloor \frac{d}{\lambda} \right\rfloor + 1 \] Ta có: \[ N_{\text{max}} = 2\left\lfloor \frac{10 \, \text{cm}}{2 \, \text{cm}} \right\rfloor + 1 = 2 \times 5 + 1 = 11 \] Như vậy, có 11 vân giao thoa cực đại xuất hiện.

4.3 Phân Tích Kết Quả Thí Nghiệm và Bài Tập

Kết quả từ thí nghiệm và bài tập trên cho thấy sự phụ thuộc của số vân giao thoa cực đại vào khoảng cách giữa các nguồn và bước sóng của sóng. Thí nghiệm Young minh họa rõ ràng cách ánh sáng giao thoa và tạo ra các vân sáng, giúp khẳng định tính chất sóng của ánh sáng. Trong khi đó, bài tập tính số vân giao thoa cực đại cho ta cái nhìn sâu hơn về mối quan hệ giữa các đại lượng vật lý trong hiện tượng giao thoa sóng.

Hiện tượng giao thoa sóng, đặc biệt là số vân giao thoa cực đại, đóng vai trò quan trọng trong việc hiểu rõ hơn về tính chất sóng của ánh sáng và các dạng sóng khác. Qua các thí nghiệm và công thức tính toán, chúng ta có thể thấy rõ sự phụ thuộc của số vân cực đại vào các yếu tố như bước sóng, khoảng cách giữa các nguồn sóng, và điều kiện giao thoa.

Việc nghiên cứu hiện tượng giao thoa không chỉ giúp chúng ta khẳng định tính chất sóng của ánh sáng mà còn mở ra nhiều ứng dụng quan trọng trong các lĩnh vực như quang học, âm học, và công nghệ laser. Hiện tượng này cũng cung cấp nền tảng cho các kỹ thuật đo lường chính xác, giúp cải thiện chất lượng cuộc sống và thúc đẩy tiến bộ công nghệ.

Tổng kết lại, giao thoa sóng là một trong những hiện tượng cơ bản và quan trọng của vật lý học, với nhiều ứng dụng thực tiễn. Số vân giao thoa cực đại không chỉ là một khái niệm lý thuyết mà còn là một công cụ mạnh mẽ trong nghiên cứu và phát triển khoa học, từ việc phân tích tính chất vật liệu đến cải thiện các hệ thống truyền thông hiện đại. Thông qua việc nắm vững các kiến thức này, chúng ta có thể ứng dụng chúng vào thực tế, góp phần nâng cao hiểu biết và phát triển công nghệ trong nhiều lĩnh vực khác nhau.