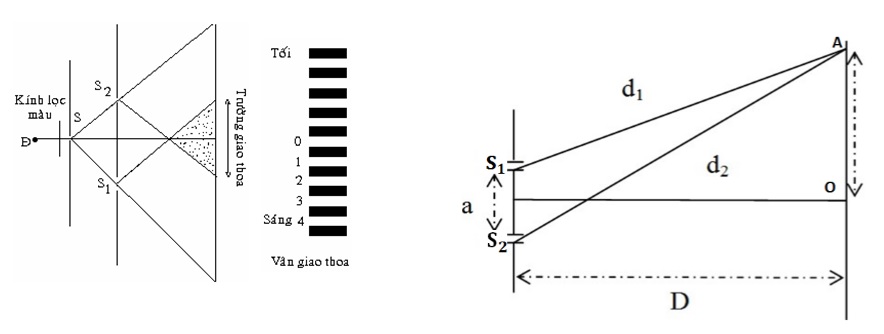
Chủ đề giải bài tập giao thoa sóng: Giải bài tập giao thoa sóng là một kỹ năng quan trọng trong môn Vật lý, đặc biệt đối với học sinh lớp 12. Bài viết này sẽ cung cấp phương pháp giải nhanh các dạng bài tập giao thoa sóng từ cơ bản đến nâng cao, bao gồm các bài tập trắc nghiệm và tự luận có lời giải chi tiết, giúp bạn nắm vững kiến thức và tự tin trong các kỳ thi.
Mục lục
Giải Bài Tập Giao Thoa Sóng - Tổng Hợp Thông Tin
Giao thoa sóng là hiện tượng phổ biến trong vật lý, xảy ra khi hai hay nhiều sóng kết hợp với nhau để tạo ra một mẫu hình sóng mới. Các bài tập về giao thoa sóng thường yêu cầu học sinh tính toán các yếu tố như biên độ, bước sóng, số điểm cực đại và cực tiểu, và vị trí của các điểm dao động. Dưới đây là tổng hợp thông tin từ các trang web cung cấp bài tập và lời giải chi tiết về hiện tượng giao thoa sóng.
Các Dạng Bài Tập Về Giao Thoa Sóng
- Bài tập cơ bản về giao thoa sóng: Các bài tập cơ bản thường bao gồm việc xác định biên độ dao động tổng hợp tại một điểm trong vùng giao thoa. Công thức phổ biến sử dụng là:
- \[ u_M = u_{1M} + u_{2M} = 2A \cos \left( \omega t + \varphi - \frac{\pi (d_1 + d_2)}{\lambda} \right) \cos \left( \frac{\pi (d_2 - d_1)}{\lambda} \right) \]
- Ví dụ: Xác định biên độ dao động tại một điểm \( M \) cách hai nguồn phát sóng \( S_1 \) và \( S_2 \) các khoảng \( d_1 \) và \( d_2 \).
Bài Tập Tính Toán Số Điểm Cực Đại và Cực Tiểu
Trong hiện tượng giao thoa sóng, các điểm dao động với biên độ cực đại và cực tiểu tạo thành các vân giao thoa. Số lượng các vân này có thể được xác định thông qua công thức:
- Số cực đại: \[ -\frac{S_1S_2}{\lambda} \leq k \leq \frac{S_1S_2}{\lambda} \]
- Số cực tiểu: \[ -\frac{S_1S_2}{\lambda} - \frac{1}{2} \leq k \leq \frac{S_1S_2}{\lambda} \]
Bài Tập Xác Định Khoảng Cách và Vị Trí Các Điểm Dao Động
Các bài tập dạng này yêu cầu học sinh tính khoảng cách giữa các điểm có dao động cực đại hoặc cực tiểu từ các nguồn phát sóng. Ví dụ:
- Ví dụ: Tính khoảng cách từ điểm \( N \) đến nguồn \( B \) trong hiện tượng giao thoa trên mặt nước.
- Lời giải: Dựa vào điều kiện cực đại giao thoa, ta có: \( MA - MB = k \lambda = NA - NB \). Suy ra \( NB = 22 \, cm \).
Ứng Dụng Các Phương Trình Sóng Trong Giải Bài Tập
Trong quá trình giải bài tập, các phương trình sóng được sử dụng để xác định các yếu tố như biên độ, tần số và bước sóng. Ví dụ, trong một bài tập yêu cầu thay đổi tần số sóng để đạt được một dạng cực đại khác, chúng ta sử dụng phương trình:
- \[ f_2 = \frac{4}{3}f_1 \]
- Điều này có nghĩa là để thay đổi từ dãy cực đại bậc ba thành dãy cực đại bậc bốn, tần số mới cần được điều chỉnh.
Kết Luận
Các bài tập về giao thoa sóng là một phần quan trọng trong việc học vật lý, giúp học sinh hiểu rõ hơn về các hiện tượng sóng và áp dụng các công thức toán học để giải quyết các vấn đề thực tế. Các trang web cung cấp lời giải chi tiết như loigiaihay.com, thuvienhoclieu.com là nguồn tài liệu hữu ích cho học sinh và giáo viên.

.png)
Lý thuyết Giao Thoa Sóng
Giao thoa sóng là một hiện tượng quan trọng trong vật lý, xảy ra khi hai hoặc nhiều sóng gặp nhau và kết hợp để tạo ra một mẫu hình sóng mới. Để hiểu rõ hơn về hiện tượng này, chúng ta cần nắm vững các khái niệm cơ bản sau đây:
- 1. Sóng kết hợp: Hai nguồn sóng được gọi là sóng kết hợp khi chúng dao động với cùng tần số, cùng phương và có hiệu số pha không đổi theo thời gian. Điều kiện này đảm bảo sự giao thoa ổn định.
- 2. Điều kiện để có giao thoa sóng:
- Hai sóng phải là sóng kết hợp, nghĩa là có cùng tần số và hiệu số pha không đổi.
- Các sóng phải gặp nhau tại cùng một điểm trong không gian.
- 3. Hiện tượng giao thoa: Hiện tượng giao thoa xảy ra khi hai sóng gặp nhau và tạo ra các điểm mà tại đó biên độ dao động của sóng tổng hợp có thể lớn nhất (cực đại) hoặc nhỏ nhất (cực tiểu). Các điểm cực đại và cực tiểu này tạo thành các vân giao thoa.
- 4. Vị trí cực đại và cực tiểu giao thoa:
- Các điểm có biên độ dao động cực đại là những điểm mà hiệu đường đi của hai sóng từ nguồn đến đó bằng một số nguyên lần bước sóng: \[ \Delta d = k\lambda \] (với \(k \in \mathbb{Z}\)).
- Các điểm có biên độ dao động cực tiểu là những điểm mà hiệu đường đi của hai sóng từ nguồn đến đó bằng một số nửa nguyên lần bước sóng: \[ \Delta d = \left(k + \frac{1}{2}\right) \lambda \] (với \(k \in \mathbb{Z}\)).
- 5. Phương trình sóng tổng hợp: Nếu hai nguồn sóng kết hợp có phương trình sóng lần lượt là \(u_1 = A \cos(\omega t + \varphi_1)\) và \(u_2 = A \cos(\omega t + \varphi_2)\), thì phương trình của sóng tổng hợp tại điểm \(M\) là: \[ u = 2A \cos\left(\frac{\varphi_1 - \varphi_2}{2}\right) \cos\left(\omega t + \frac{\varphi_1 + \varphi_2}{2}\right). \]
- 6. Ứng dụng của hiện tượng giao thoa sóng: Hiện tượng giao thoa sóng có nhiều ứng dụng thực tế, từ việc giải thích màu sắc của váng dầu trên mặt nước đến các công nghệ tiên tiến như interferometer (máy đo giao thoa) trong vật lý lượng tử, quang học và truyền thông.
Hiểu rõ lý thuyết về giao thoa sóng giúp học sinh và người học vật lý nắm vững kiến thức và áp dụng vào giải quyết các bài tập cũng như hiểu rõ các hiện tượng sóng trong đời sống.
Phương Pháp Giải Các Bài Tập Giao Thoa Sóng
Để giải quyết các bài tập về giao thoa sóng, chúng ta cần nắm vững các khái niệm cơ bản về sóng và hiện tượng giao thoa. Dưới đây là các phương pháp giải chi tiết và từng bước cho các dạng bài tập thường gặp trong giao thoa sóng:
1. Xác Định Số Điểm Dao Động Cực Đại - Cực Tiểu Giữa Hai Nguồn
- Hai nguồn cùng pha:
Công thức tính số điểm dao động cực đại và cực tiểu giữa hai nguồn được xác định như sau:
- Số điểm dao động cực đại: \( - \dfrac{l}{\lambda } < k < \dfrac{l}{\lambda }\) với \(k \in \mathbb{Z}\).
- Số điểm dao động cực tiểu: \( - \dfrac{l}{\lambda } - \dfrac{1}{2} < k < \dfrac{l}{\lambda } - \dfrac{1}{2}\) với \(k \in \mathbb{Z}\).
- Hai nguồn ngược pha:
Khi hai nguồn dao động ngược pha (\(\Delta \varphi = \pi\)), số điểm dao động cực đại và cực tiểu được tính như sau:
- Điểm dao động cực đại: \({d_1}-{\rm{ }}{d_2} = \left( {2k + 1} \right)\dfrac{\lambda }{2}\) với \(k \in \mathbb{Z}\).
- Điểm dao động cực tiểu: \({d_1}-{\rm{ }}{d_2} = k\lambda\) với \(k \in \mathbb{Z}\).
2. Xác Định Vị Trí Giao Thoa Cực Đại - Cực Tiểu Trên Đoạn Thẳng Nối Hai Nguồn
Để xác định vị trí các điểm có dao động cực đại và cực tiểu trên một đoạn thẳng nối hai nguồn, ta cần áp dụng các công thức tương tự như trên, nhưng điều chỉnh phạm vi và điều kiện cho các giá trị \(k\).
3. Xác Định Vị Trí Của Các Điểm Giao Thoa Trên Đường Tròn hoặc Hình Chữ Nhật
- Đường tròn: Phân tích trên các cung tròn và sử dụng định lý Pitago để tìm các điểm tương ứng có giao thoa sóng.
- Hình chữ nhật: Chia hình chữ nhật thành các đoạn thẳng nối hai nguồn, áp dụng phương pháp tương tự như với đoạn thẳng.
4. Phương Pháp Xác Định Các Điểm Cùng Pha hoặc Ngược Pha Với Hai Nguồn
Các điểm dao động cùng pha hoặc ngược pha với hai nguồn có thể được xác định bằng cách sử dụng các điều kiện giao thoa tương ứng, như việc phân tích pha dao động (\(\Delta \varphi\)).
5. Phương Pháp Giải Các Dạng Bài Tập Liên Quan Đến Sóng Dừng và Sóng Âm
- Giải các bài tập xác định vị trí cực đại và cực tiểu sóng dừng.
- Xác định số điểm dao động trên một sợi dây hoặc đường thẳng cho trước.
Trên đây là một số phương pháp giải các bài tập về giao thoa sóng. Hãy áp dụng linh hoạt các công thức và hiểu rõ các khái niệm cơ bản để giải quyết hiệu quả mọi dạng bài tập liên quan.

Các Bài Tập Mẫu và Giải Chi Tiết
Dưới đây là một số bài tập mẫu về hiện tượng giao thoa sóng điển hình và lời giải chi tiết. Các bài tập này được chia theo từng dạng cụ thể để giúp học sinh có thể nắm bắt kiến thức và phương pháp giải một cách rõ ràng.
Bài Tập 1: Xác Định Vị Trí Cực Đại và Cực Tiểu
Đề bài: Hai nguồn sóng \(S_1\) và \(S_2\) dao động cùng pha và có bước sóng \(\lambda = 4cm\). Tìm số điểm dao động cực đại và cực tiểu trên đoạn thẳng nối hai nguồn với khoảng cách \(S_1S_2 = 20cm\).
Giải:
- Tính số điểm dao động cực đại giữa hai nguồn: \[ -\dfrac{l}{\lambda} < k < \dfrac{l}{\lambda} \Rightarrow -\dfrac{20}{4} < k < \dfrac{20}{4} \] Từ đó, ta có \(k\) chạy từ -5 đến 5 (11 điểm cực đại).
- Tính số điểm dao động cực tiểu giữa hai nguồn: \[ -\dfrac{l}{\lambda} - \dfrac{1}{2} < k < \dfrac{l}{\lambda} - \dfrac{1}{2} \Rightarrow -5.5 < k < 4.5 \] Từ đó, ta có \(k\) chạy từ -5 đến 4 (10 điểm cực tiểu).
Bài Tập 2: Tính Khoảng Cách Giữa Các Vị Trí Cực Đại Liên Tiếp
Đề bài: Trong một thí nghiệm giao thoa sóng trên mặt nước với hai nguồn kết hợp \(S_1\) và \(S_2\) dao động cùng pha, bước sóng \(\lambda = 5cm\). Tính khoảng cách giữa hai điểm cực đại liên tiếp trên đường nối hai nguồn.
Giải:
- Khoảng cách giữa hai điểm cực đại liên tiếp trên đường nối hai nguồn được xác định bởi công thức: \[ \Delta d = \dfrac{\lambda}{2} \]
- Với \(\lambda = 5cm\), ta có: \[ \Delta d = \dfrac{5}{2} = 2.5cm \] Vậy, khoảng cách giữa hai điểm cực đại liên tiếp là \(2.5cm\).
Bài Tập 3: Xác Định Vị Trí Cực Đại Giao Thoa Trên Đoạn Thẳng
Đề bài: Hai nguồn sóng \(S_1\) và \(S_2\) dao động ngược pha nhau, khoảng cách giữa hai nguồn là \(d = 12cm\), bước sóng là \(\lambda = 3cm\). Hãy xác định vị trí các điểm dao động cực đại trên đoạn thẳng nối hai nguồn.
Giải:
- Do hai nguồn ngược pha, vị trí các điểm dao động cực đại được xác định bởi công thức: \[ \Delta d = \left(2k + 1\right)\dfrac{\lambda}{2}, \, k \in \mathbb{Z} \]
- Tính toán các giá trị của \(k\) để xác định vị trí các điểm dao động cực đại nằm trên đoạn \(S_1S_2\) từ 0 đến 12cm:
- Với \(k = 0\): \( \Delta d = 1.5cm\)
- Với \(k = 1\): \( \Delta d = 4.5cm\)
- Với \(k = 2\): \( \Delta d = 7.5cm\)
- Với \(k = 3\): \( \Delta d = 10.5cm\)
Trên đây là các bài tập mẫu và lời giải chi tiết về giao thoa sóng. Hãy nắm vững các công thức và phương pháp để giải quyết tốt các bài tập tương tự.

Các Đề Thi Về Giao Thoa Sóng
Dưới đây là tổng hợp một số đề thi điển hình về giao thoa sóng từ các kỳ thi học kỳ, thi thử THPT Quốc gia và các kỳ thi học sinh giỏi. Các đề thi này được phân loại theo cấp độ và kèm theo hướng dẫn giải chi tiết để học sinh có thể ôn tập và chuẩn bị tốt nhất cho các kỳ thi sắp tới.
Đề Thi 1: Đề Thi Thử THPT Quốc Gia Môn Vật Lý - Chuyên Đề Giao Thoa Sóng
Câu 1: Hai nguồn sóng \(S_1\) và \(S_2\) trên mặt nước dao động với cùng biên độ, cùng tần số và cùng pha. Biết khoảng cách giữa hai nguồn \(d = 20cm\) và bước sóng \(\lambda = 4cm\). Tìm số điểm dao động cực đại và cực tiểu trên đoạn thẳng nối hai nguồn.
Hướng dẫn giải:
- Áp dụng công thức tính số điểm dao động cực đại: \[ N_{max} = 2 \left( \dfrac{d}{\lambda} \right) + 1 = 11. \]
- Áp dụng công thức tính số điểm dao động cực tiểu: \[ N_{min} = 2 \left( \dfrac{d}{\lambda} - \dfrac{1}{2} \right) = 10. \]
Đề Thi 2: Đề Thi Học Kỳ Môn Vật Lý Lớp 12 - Chuyên Đề Sóng Cơ
Câu 2: Trên mặt nước có hai nguồn sóng \(S_1\) và \(S_2\) dao động cùng pha, bước sóng \(\lambda = 6cm\). Tính khoảng cách từ trung điểm của \(S_1S_2\) đến điểm dao động cực đại gần nhất.
Hướng dẫn giải:
- Khoảng cách từ trung điểm đến điểm dao động cực đại gần nhất là \(\dfrac{\lambda}{4}\).
- Thay giá trị \(\lambda = 6cm\) vào, ta có: \[ \dfrac{6}{4} = 1.5cm. \]
Đề Thi 3: Đề Thi Học Sinh Giỏi Tỉnh Môn Vật Lý - Giao Thoa Sóng Trên Mặt Nước
Câu 3: Cho hai nguồn sóng \(S_1\) và \(S_2\) dao động ngược pha với bước sóng \(\lambda = 8cm\) và khoảng cách \(d = 24cm\). Hãy xác định số điểm dao động cực đại trên đoạn thẳng nối hai nguồn.
Hướng dẫn giải:
- Với hai nguồn dao động ngược pha, điều kiện để có giao thoa cực đại là: \[ |S_1M - S_2M| = (2k+1)\dfrac{\lambda}{2}, k \in \mathbb{Z}. \]
- Thay giá trị vào và tìm các giá trị \(k\) phù hợp để xác định số điểm dao động cực đại.
Đề Thi 4: Đề Thi Học Kỳ Môn Vật Lý Lớp 11 - Chuyên Đề Giao Thoa Sóng Âm
Câu 4: Trong một thí nghiệm giao thoa sóng âm, hai nguồn phát ra âm thanh cùng pha với tần số \(f = 500Hz\), tốc độ truyền âm trong không khí là \(v = 340m/s\). Tính khoảng cách giữa hai điểm cực đại âm gần nhất.
Hướng dẫn giải:
- Tính bước sóng \(\lambda\) từ công thức: \[ \lambda = \dfrac{v}{f} = \dfrac{340}{500} = 0.68m. \]
- Khoảng cách giữa hai điểm cực đại gần nhất là: \[ \dfrac{\lambda}{2} = 0.34m. \]
Các đề thi và hướng dẫn giải trên đây giúp học sinh có thể luyện tập, hiểu rõ các khái niệm về giao thoa sóng và chuẩn bị tốt cho các kỳ thi quan trọng. Hãy tự tin và làm quen với nhiều dạng bài tập khác nhau để nâng cao kỹ năng giải bài.

Ứng Dụng Thực Tiễn của Hiện Tượng Giao Thoa Sóng
Hiện tượng giao thoa sóng không chỉ là một hiện tượng thú vị trong vật lý lý thuyết mà còn có nhiều ứng dụng thực tiễn quan trọng trong nhiều lĩnh vực khác nhau. Dưới đây là một số ứng dụng nổi bật của hiện tượng này:
1. Giao thoa sóng trong Công nghệ và Kỹ thuật
Trong lĩnh vực công nghệ và kỹ thuật, giao thoa sóng được sử dụng trong nhiều thiết bị và công nghệ hiện đại:
- Giao thoa kế (Interferometer): Các thiết bị này sử dụng nguyên lý giao thoa sóng để đo khoảng cách, độ dài hoặc các biến dạng rất nhỏ với độ chính xác cao.
- Kỹ thuật đo lường chính xác: Giao thoa sóng ánh sáng được sử dụng trong các kỹ thuật đo lường tiên tiến như trong chế tạo và kiểm tra các chi tiết máy móc.
- Hệ thống radar: Sự giao thoa của sóng radar được sử dụng để phát hiện và định vị các vật thể trong khoảng cách xa, đặc biệt trong hàng không và quân sự.
2. Hiện tượng giao thoa sóng trong tự nhiên và môi trường
Trong tự nhiên, giao thoa sóng xuất hiện dưới nhiều dạng khác nhau:
- Sóng biển: Hiện tượng giao thoa sóng nước có thể quan sát dễ dàng trên mặt biển, tạo ra các vùng sóng cao và vùng lặng sóng.
- Hiện tượng sóng dừng: Trong các dòng sông hoặc trong lòng các ống dẫn nước, sự giao thoa của sóng nước có thể tạo ra các nút và bụng sóng, ảnh hưởng đến dòng chảy và cấu trúc dòng chảy.
3. Ứng dụng trong truyền thông và viễn thông
Giao thoa sóng có vai trò quan trọng trong lĩnh vực truyền thông và viễn thông:
- Giao thoa trong mạng quang: Trong các hệ thống thông tin quang học, hiện tượng giao thoa được sử dụng để truyền tín hiệu trên các bước sóng khác nhau, giúp tối ưu hóa băng thông và tăng hiệu quả truyền dữ liệu.
- Kỹ thuật anten: Giao thoa sóng được ứng dụng trong thiết kế và bố trí anten để tối ưu hóa tín hiệu phát và nhận, đặc biệt trong các hệ thống viễn thông di động.
4. Ứng dụng trong Y học: Siêu âm và chẩn đoán hình ảnh
Trong y học, hiện tượng giao thoa sóng được ứng dụng rộng rãi trong chẩn đoán và điều trị:
- Siêu âm: Sự giao thoa của sóng siêu âm được sử dụng để tạo ra hình ảnh bên trong cơ thể, giúp bác sĩ chẩn đoán các bệnh lý và theo dõi sự phát triển của thai nhi.
- Điều trị bằng sóng âm: Giao thoa sóng âm được sử dụng trong điều trị bằng sóng âm tần số cao, giúp phá vỡ sỏi thận hoặc loại bỏ các mô bệnh.
Nhờ các ứng dụng đa dạng này, hiện tượng giao thoa sóng đã chứng minh được giá trị quan trọng trong đời sống và công nghệ, góp phần vào sự phát triển của khoa học và các ngành công nghiệp hiện đại.