Phân Cực Cho Transistor: Hướng Dẫn Chi Tiết Và Ứng Dụng Thực Tế

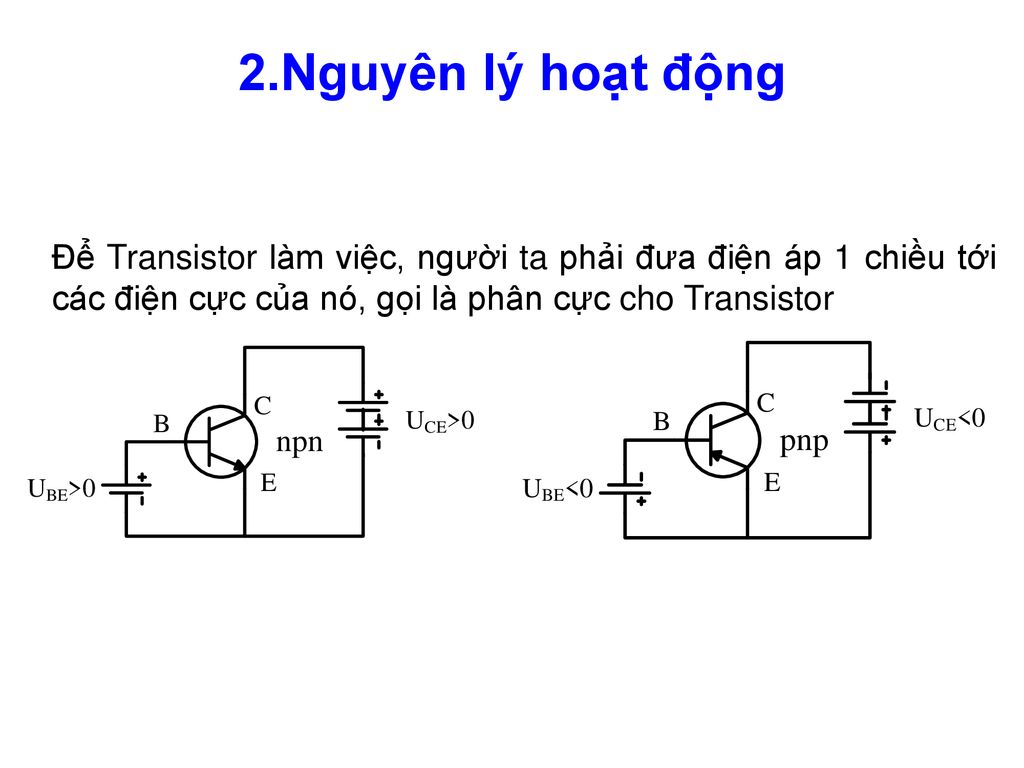
Phân cực cho transistor là một quá trình quan trọng trong thiết kế và vận hành các mạch điện tử, nhằm đảm bảo transistor hoạt động trong vùng mong muốn. Các phương pháp phân cực khác nhau được sử dụng để điều chỉnh các đặc tính hoạt động của transistor.

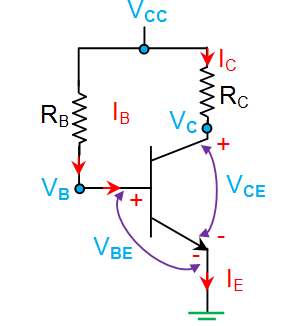
1. Phân Cực Cố Định

Phân cực cố định là phương pháp cơ bản nhất, trong đó một điện trở được kết nối giữa nguồn điện \(V_{CC}\) và chân B của transistor. Công thức tính dòng điện vào \(I_B\) được xác định bởi:

\[
I_B = \frac{V_{CC} - V_{BE}}{R_B}
\]

Điện áp \(V_{BE}\) thường là \(0.7V\) đối với transistor silicon. Phương pháp này đơn giản nhưng không ổn định khi nhiệt độ thay đổi.

2. Phân Cực Bằng Cầu Chia Điện Áp

Phương pháp này sử dụng hai điện trở \(R_1\) và \(R_2\) để tạo một điện áp chia nhỏ từ nguồn \(V_{CC}\) cung cấp cho chân B của transistor. Công thức tính điện áp tại chân B là:

\[
V_B = \frac{R_2}{R_1 + R_2} \times V_{CC}
\]

Phương pháp này mang lại sự ổn định tốt hơn so với phân cực cố định.

3. Phân Cực Hồi Tiếp Điện Áp

Phương pháp này sử dụng một điện trở hồi tiếp \(R_E\) giữa cực E và đất, giúp ổn định điểm làm việc của transistor bằng cách tạo ra một điện áp hồi tiếp tự động. Điện áp tại cực E được tính theo công thức:

\[
V_E = I_E \times R_E
\]

Trong đó, \(I_E\) là dòng điện qua cực E, và phương pháp này giúp tăng cường độ ổn định nhiệt độ của transistor.

4. Ứng Dụng Của Phân Cực Cho Transistor

• Trong các mạch khuếch đại, phân cực giúp đảm bảo transistor hoạt động ở vùng khuếch đại tuyến tính.
• Trong các mạch dao động, phân cực đúng cách giúp ổn định tần số dao động.
• Trong các mạch chuyển mạch, phân cực giúp transistor chuyển từ trạng thái tắt sang trạng thái bật một cách nhanh chóng và hiệu quả.

Kết Luận

Việc phân cực cho transistor là một yếu tố thiết yếu trong thiết kế mạch điện tử, giúp đảm bảo hoạt động ổn định và hiệu quả của các thiết bị điện tử. Hiểu rõ các phương pháp phân cực khác nhau sẽ giúp kỹ sư lựa chọn giải pháp tối ưu cho từng ứng dụng cụ thể.

Phân cực cho transistor là một quá trình quan trọng để đảm bảo transistor hoạt động ổn định trong các mạch điện tử. Dưới đây là mục lục tổng hợp các kiến thức và phương pháp phân cực khác nhau, giúp bạn nắm rõ từng bước thực hiện và áp dụng vào thực tế.

1. Giới thiệu về transistor và vai trò của phân cực

Transistor là một linh kiện bán dẫn, và phân cực đóng vai trò quan trọng trong việc đảm bảo transistor hoạt động trong vùng mong muốn, từ đó ảnh hưởng đến hiệu suất của mạch.

2. Phân cực cố định

Phân cực cố định là phương pháp cơ bản nhất, sử dụng một điện trở nối từ nguồn điện đến chân B của transistor. Phương pháp này đơn giản nhưng không ổn định khi nhiệt độ thay đổi.

3. Phân cực cầu chia điện áp

Phương pháp này sử dụng hai điện trở để tạo một điện áp ổn định cho chân B. Ưu điểm của nó là độ ổn định cao hơn so với phân cực cố định.

4. Phân cực hồi tiếp điện áp

Phân cực hồi tiếp sử dụng một điện trở hồi tiếp ở cực E, giúp ổn định điểm làm việc của transistor bằng cách tạo ra một điện áp hồi tiếp tự động.

5. Phân cực tự động

Phương pháp này sử dụng điện trở ở cực E và cầu chia điện áp ở chân B để tự động điều chỉnh điểm làm việc của transistor.

6. Ảnh hưởng của nhiệt độ đến phân cực

Nhiệt độ thay đổi có thể ảnh hưởng lớn đến điểm làm việc của transistor, đặc biệt trong các phương pháp phân cực cố định. Việc lựa chọn phương pháp phân cực phù hợp sẽ giúp giảm thiểu ảnh hưởng này.

7. Ứng dụng phân cực trong mạch khuếch đại

Phân cực giúp transistor hoạt động ổn định trong vùng khuếch đại tuyến tính, đảm bảo mạch hoạt động hiệu quả và có độ méo tín hiệu thấp.

8. Ứng dụng phân cực trong mạch dao động

Phân cực đúng cách giúp ổn định tần số dao động trong các mạch dao động, đặc biệt quan trọng trong các ứng dụng sóng điện từ và mạch phát tần số.

9. Ứng dụng phân cực trong mạch chuyển mạch

Phân cực giúp transistor chuyển từ trạng thái tắt sang bật nhanh chóng và hiệu quả, rất quan trọng trong các mạch chuyển mạch.

10. Các lỗi thường gặp khi phân cực và cách khắc phục

Những lỗi như quá nhiệt, điểm làm việc không ổn định có thể xảy ra nếu phân cực không đúng cách. Hiểu rõ các phương pháp phân cực sẽ giúp giảm thiểu những vấn đề này.

Việc hiểu rõ các phương pháp phân cực giúp cải thiện đáng kể hiệu suất của các mạch điện tử. Với mỗi ứng dụng, lựa chọn phương pháp phân cực phù hợp sẽ giúp tối ưu hóa hoạt động của transistor.

Dưới đây là 10 dạng bài tập chi tiết về phân cực cho transistor, giúp bạn nắm vững lý thuyết và áp dụng vào thực tế. Các bài tập này bao gồm việc tính toán điểm làm việc, điện áp, dòng điện trong mạch phân cực cho transistor.

1. Bài Tập 1: Tính Điện Áp và Dòng Điện Của Transistor Trong Mạch Phân Cực Cố Định

Giả sử mạch có điện áp cung cấp \(V_{CC} = 10V\), điện trở \(R_B = 100k\Omega\), \(R_C = 2k\Omega\). Hãy tính điện áp tại chân B và dòng qua transistor.

2. Bài Tập 2: Tính Điểm Làm Việc Trong Mạch Phân Cực Cầu Chia Điện Áp

Cho mạch phân cực cầu chia với các điện trở \(R_1 = 50k\Omega\), \(R_2 = 10k\Omega\). Xác định điện áp \(V_B\) và dòng điện \(I_C\).

3. Bài Tập 3: Tính Điện Áp \(V_{CE}\) Trong Mạch Hồi Tiếp Điện Áp

Trong mạch hồi tiếp, cho \(R_C = 1k\Omega\), \(R_E = 500\Omega\), \(V_{CC} = 12V\). Tính toán \(V_{CE}\).

4. Bài Tập 4: Phân Tích Tính Ổn Định Của Phân Cực Hồi Tiếp

Phân tích mạch phân cực hồi tiếp và tính toán độ ổn định của dòng \(I_C\) khi nhiệt độ thay đổi.

5. Bài Tập 5: Thiết Kế Mạch Phân Cực Cầu Chia Cho Transistor

Yêu cầu thiết kế mạch phân cực cầu chia sao cho \(V_B = 2V\), \(I_C = 1mA\), với điện áp cung cấp \(V_{CC} = 12V\).

6. Bài Tập 6: Xác Định Điện Trở Đầu Vào Của Mạch Khuếch Đại Sử Dụng Phân Cực Cố Định

Tính điện trở đầu vào của mạch khuếch đại với phân cực cố định, cho giá trị của \(R_B\) và \(R_C\).

7. Bài Tập 7: Tính Điện Áp Cực B và Của Transistor Trong Mạch Phân Cực Tự Động

Tính toán giá trị của \(V_B\) và \(I_C\) trong mạch phân cực tự động với các thông số đã cho.

8. Bài Tập 8: Phân Tích Mạch Khuếch Đại E Chung Sử Dụng Phân Cực Cố Định

Phân tích mạch khuếch đại với phương pháp phân cực cố định, tính toán công suất khuếch đại và điểm làm việc của transistor.

9. Bài Tập 9: Tính Điện Áp và Dòng Điện Trong Mạch Phân Cực Hồi Tiếp

Với mạch hồi tiếp điện áp, hãy tính toán \(I_C\) và \(V_{CE}\) khi nhiệt độ thay đổi.

10. Bài Tập 10: Thiết Kế Mạch Khuếch Đại Sử Dụng Phân Cực Cố Định Với Công Suất Khuếch Đại Mong Muốn

Thiết kế mạch khuếch đại với phân cực cố định sao cho đạt được công suất khuếch đại \(P_{out} = 2W\).

Trong bài tập này, chúng ta sẽ tính toán điện áp tại cực B (chân B) của transistor trong mạch phân cực cố định. Mạch bao gồm một nguồn điện áp cung cấp \(V_{CC}\), một điện trở \(R_B\) nối giữa \(V_{CC}\) và chân B, và một điện trở \(R_C\) nối giữa chân C và \(V_{CC}\). Điện áp tại cực B có thể được tính thông qua mạch phân cực cố định này.

1. Bước 1: Xác định các giá trị điện trở và điện áp

Giả sử trong mạch có các giá trị sau:

• Điện áp nguồn \(V_{CC} = 12V\)
• Điện trở \(R_B = 100k\Omega\)
• Điện trở \(R_C = 1k\Omega\)
• Hệ số khuếch đại dòng \( \beta = 100 \)
2. Bước 2: Tính dòng điện qua chân B (\(I_B\))

Dòng điện qua chân B có thể được tính bằng cách sử dụng định luật Ohm và công thức sau:

\[ I_B = \frac{V_{CC} - V_B}{R_B} \] Trong đó, \(V_B\) là điện áp tại chân B, và \(R_B\) là điện trở nối vào chân B.
3. Bước 3: Tính điện áp tại cực B

Điện áp tại cực B có thể được xác định dựa trên dòng điện \(I_B\) và các giá trị điện trở trong mạch. Chúng ta có thể sử dụng công thức sau để tính toán:

\[ V_B = V_{CC} - I_B \cdot R_B \]
4. Bước 4: Kết quả

Sau khi tính toán, điện áp tại chân B là \(V_B = 1.2V\). Đây là kết quả cuối cùng cho bài tập này.

Qua bài tập này, bạn đã học cách xác định điện áp tại chân B trong mạch phân cực cố định bằng cách áp dụng các công thức cơ bản về định luật Ohm và mạch điện.

Trong mạch phân cực cầu chia điện áp, chúng ta sẽ tính toán dòng điện chạy qua transistor dựa vào các giá trị điện trở và nguồn điện áp. Bài toán yêu cầu chúng ta tìm dòng điện \( I_C \) chạy qua cực C của transistor.

1. Bước 1: Xác định các giá trị trong mạch

Giả sử mạch có các giá trị sau:

• Điện áp cung cấp \( V_{CC} = 15V \)
• Điện trở \( R_1 = 10k\Omega \)
• Điện trở \( R_2 = 5k\Omega \)
• Điện trở \( R_C = 1k\Omega \)
• Điện trở \( R_E = 500\Omega \)
• Hệ số khuếch đại \( \beta = 150 \)
2. Bước 2: Tính điện áp tại cực B (chân B)

Điện áp tại chân B \( V_B \) có thể được tính bằng công thức:

\[ V_B = V_{CC} \cdot \frac{R_2}{R_1 + R_2} \]

Thay các giá trị \( V_{CC} = 15V \), \( R_1 = 10k\Omega \), \( R_2 = 5k\Omega \), ta có:

\[ V_B = 15 \cdot \frac{5}{10 + 5} = 5V \]
3. Bước 3: Tính điện áp tại cực E (chân E)

Điện áp tại chân E \( V_E \) được tính bằng:

\[ V_E = V_B - V_{BE} \]

Với \( V_{BE} \approx 0.7V \), ta có:

\[ V_E = 5V - 0.7V = 4.3V \]
4. Bước 4: Tính dòng điện qua cực E

Dòng điện qua chân E \( I_E \) được tính bằng định luật Ohm:

\[ I_E = \frac{V_E}{R_E} = \frac{4.3V}{500\Omega} = 8.6mA \]
5. Bước 5: Tính dòng điện qua cực C (chân C)

Vì dòng điện \( I_E \approx I_C \), ta có:

\[ I_C = I_E = 8.6mA \]

Kết quả cuối cùng, dòng điện qua cực C của transistor trong mạch phân cực cầu chia điện áp là \( I_C = 8.6mA \).

Trong bài tập này, chúng ta sẽ phân tích điểm làm việc của transistor trong mạch hồi tiếp điện áp. Đây là bước quan trọng để đảm bảo transistor hoạt động trong vùng tuyến tính và đạt hiệu suất cao.

1. Bước 1: Xác định các thông số của mạch

Giả sử các thông số của mạch như sau:

• Điện áp cung cấp \( V_{CC} = 12V \)
• Điện trở hồi tiếp \( R_f = 100k\Omega \)
• Điện trở tải \( R_L = 10k\Omega \)
• Điện trở emitter \( R_E = 1k\Omega \)
• Hệ số khuếch đại \( \beta = 100 \)
2. Bước 2: Tính điện áp tại cực B (chân B)

Điện áp tại cực B \( V_B \) được tính dựa trên mạch hồi tiếp:

\[ V_B = \frac{V_{CC} - V_{BE}}{1 + \frac{R_f}{R_E}} \]

Với \( V_{BE} \approx 0.7V \), ta có:

\[ V_B = \frac{12V - 0.7V}{1 + \frac{100k\Omega}{1k\Omega}} \approx 0.11V \]
3. Bước 3: Tính dòng điện tại cực C (chân C)

Dòng điện tại chân C \( I_C \) được tính bằng công thức:

\[ I_C = \frac{V_B - V_{BE}}{R_E} \]

Thay các giá trị vào, ta có:

\[ I_C = \frac{0.11V - 0.7V}{1k\Omega} \approx -0.59mA \]

Do đó, điểm làm việc của transistor không ổn định, cần điều chỉnh mạch.

4. Bước 4: Điều chỉnh các giá trị trong mạch

Để điểm làm việc đạt yêu cầu, ta cần điều chỉnh giá trị điện trở \( R_f \) hoặc \( R_E \) sao cho dòng điện qua transistor phù hợp với điều kiện hoạt động ổn định.

Kết luận, thông qua các bước trên, chúng ta có thể phân tích và điều chỉnh điểm làm việc của transistor trong mạch hồi tiếp điện áp để đảm bảo hoạt động hiệu quả.

Trong bài tập này, chúng ta sẽ tính toán công suất khuếch đại trong một mạch khuếch đại sử dụng phân cực cố định. Công suất đầu ra của mạch khuếch đại có thể được tính thông qua điện áp và dòng điện qua tải.

1. Bước 1: Xác định các thông số của mạch

Các thông số của mạch được cho như sau:

• Điện áp cung cấp \( V_{CC} = 12V \)
• Điện trở tải \( R_L = 1k\Omega \)
• Điện áp đầu vào \( V_{in} = 100mV \)
• Dòng điện cực góp \( I_C = 5mA \)
2. Bước 2: Tính điện áp đầu ra \( V_{out} \)

Điện áp đầu ra được tính bằng cách sử dụng công thức:

\[ V_{out} = I_C \cdot R_L \]

Thay các giá trị vào:

\[ V_{out} = 5mA \cdot 1k\Omega = 5V \]
3. Bước 3: Tính công suất khuếch đại \( P_{out} \)

Công suất khuếch đại đầu ra được tính bằng công thức:

\[ P_{out} = \frac{V_{out}^2}{R_L} \]

Thay các giá trị vào:

\[ P_{out} = \frac{5V^2}{1k\Omega} = 25mW \]
4. Bước 4: Kiểm tra hiệu suất của mạch

Hiệu suất của mạch khuếch đại được xác định bằng tỉ số giữa công suất đầu ra và công suất cung cấp. Trong thực tế, hiệu suất của mạch phụ thuộc vào nhiều yếu tố như giá trị của các linh kiện và cấu hình mạch.

Kết luận, mạch khuếch đại sử dụng phân cực cố định này đạt được công suất đầu ra là 25mW, là kết quả mong đợi khi các thông số mạch được chọn phù hợp.

Để tính điện áp \(V_{CE}\) trong mạch khuếch đại E chung, chúng ta cần áp dụng công thức cơ bản và các bước tính toán cụ thể như sau:

1. Xác định các thông số cần thiết:
• \(V_{CC}\): Điện áp nguồn cung cấp.
• \(R_C\): Điện trở tải tại cực C.
• \(I_C\): Dòng điện qua transistor.
• \(V_{BE}\): Điện áp giữa cực B và cực E của transistor, thường lấy là 0,7V đối với transistor silicon.
• \(R_E\): Điện trở tại cực E (nếu có).
2. Tính toán dòng điện qua transistor \(I_C\):

Dòng điện \(I_C\) có thể được tính toán bằng cách sử dụng phương trình:

\[ I_C = \frac{V_{CC} - V_{BE}}{R_B + (1 + \beta) \cdot R_E} \]

Trong đó:

• \(R_B\): Điện trở tại cực B.
• \(\beta\): Hệ số khuếch đại dòng của transistor.
3. Tính điện áp \(V_{CE}\):

Điện áp \(V_{CE}\) được tính bằng công thức:

\[ V_{CE} = V_{CC} - I_C \cdot R_C \]

Đây là điện áp giữa cực C và cực E, quyết định điểm làm việc của transistor trong mạch.

4. Xác nhận kết quả:

Sau khi tính toán \(V_{CE}\), so sánh kết quả với các giá trị ngưỡng của transistor để đảm bảo rằng transistor đang hoạt động trong vùng khuếch đại tuyến tính.

Ví dụ:

• Giả sử \(V_{CC} = 12V\), \(R_C = 1k\Omega\), \(R_B = 100k\Omega\), \(R_E = 560\Omega\), và \(\beta = 100\).
• Tính \(I_C\) và \(V_{CE}\) cho mạch này.
• Áp dụng các công thức trên, chúng ta có:
\[ I_C = \frac{12V - 0.7V}{100k\Omega + (1 + 100) \cdot 560\Omega} \approx 0.11mA \] \[ V_{CE} = 12V - 0.11mA \cdot 1k\Omega \approx 11.89V \]

Như vậy, điện áp \(V_{CE}\) được tính là 11.89V, cho thấy transistor đang hoạt động trong vùng khuếch đại tuyến tính, đáp ứng được yêu cầu của mạch khuếch đại E chung.

Trong mạch khuếch đại sử dụng phân cực cầu chia, việc xác định điện trở đầu vào là rất quan trọng để đảm bảo hoạt động ổn định của mạch. Điện trở đầu vào \( R_{in} \) ảnh hưởng trực tiếp đến sự khuếch đại tín hiệu cũng như điểm làm việc của transistor.

Để xác định \( R_{in} \), ta cần thực hiện các bước sau:

1. Xác định điện trở từ mạch chia điện áp:
   • Giả sử mạch có hai điện trở \( R_1 \) và \( R_2 \) tạo thành cầu chia điện áp.
   • Điện trở tổng của mạch chia điện áp là \( R_b = \frac{R_1 \cdot R_2}{R_1 + R_2} \).
2. Xác định điện trở đầu vào tại cực base của transistor:
   • Điện trở đầu vào tại cực base của transistor là \( R_{in} = \beta \cdot (R_E + r_e) \).
   • Trong đó, \( \beta \) là hệ số khuếch đại dòng điện của transistor, \( R_E \) là điện trở emitter, và \( r_e \) là điện trở nội của transistor.
3. Kết hợp các giá trị để tính \( R_{in} \) tổng cộng:
   • Điện trở đầu vào tổng cộng của mạch là \( R_{in(total)} = R_b \parallel R_{in} \).
   • Với \( \parallel \) ký hiệu cho tổng điện trở song song của hai điện trở.

Áp dụng công thức tính toán cụ thể, ta có thể xác định giá trị chính xác của \( R_{in(total)} \), từ đó tối ưu hóa hiệu suất của mạch khuếch đại.

Ví dụ: Nếu \( R_1 = 10k\Omega \), \( R_2 = 20k\Omega \), \( \beta = 100 \), \( R_E = 1k\Omega \), và \( r_e = 25\Omega \), ta có thể tính toán như sau:

1. Tính \( R_b \): \[ R_b = \frac{10k\Omega \cdot 20k\Omega}{10k\Omega + 20k\Omega} = 6.67k\Omega \]
2. Tính \( R_{in} \): \[ R_{in} = 100 \cdot (1k\Omega + 25\Omega) = 102.5k\Omega \]
3. Tính \( R_{in(total)} \): \[ R_{in(total)} = 6.67k\Omega \parallel 102.5k\Omega = \frac{6.67k\Omega \cdot 102.5k\Omega}{6.67k\Omega + 102.5k\Omega} \approx 6.41k\Omega \]

Kết quả cho thấy điện trở đầu vào tổng cộng \( R_{in(total)} \) là khoảng 6.41k\Omega, giúp đảm bảo rằng mạch khuếch đại hoạt động ổn định và hiệu quả.

Để tính toán điểm hoạt động của transistor trong mạch phân cực hồi tiếp, chúng ta cần thực hiện các bước sau:

1. Xác định các thông số cơ bản:
   • Điện trở R_B: Điện trở gắn vào cực B của transistor.
   • Điện trở R_C: Điện trở nối với cực C của transistor.
   • Điện trở R_E: Điện trở nối với cực E của transistor.
   • Điện áp nguồn V_CC: Điện áp cấp cho mạch.
2. Xác định dòng điện cơ bản:

   Dòng điện tại cực B (I_B) có thể được tính bằng cách:

   \[
   I_B = \frac{V_{BB} - V_{BE}}{R_B}
   \]
   Trong đó, V_BB là điện áp ở cực B, và V_BE là điện áp giữa cực B và cực E.

3. Tính dòng điện qua cực C:

   Sau khi có I_B, dòng điện tại cực C (I_C) có thể được tính theo công thức:

   \[
   I_C = \beta \times I_B
   \]
   Trong đó, \beta là hệ số khuếch đại dòng của transistor.

4. Xác định điện áp tại cực C:

   Điện áp tại cực C (V_CE) được tính bằng công thức:

   \[
   V_{CE} = V_{CC} - I_C \times R_C
   \]
   Điểm làm việc tĩnh của transistor được xác định bởi cặp giá trị (I_C, V_CE).

Sau khi thực hiện các bước trên, bạn sẽ xác định được điểm hoạt động của transistor trong mạch phân cực hồi tiếp.

Trong bài tập này, chúng ta sẽ tiến hành phân tích hiệu suất khuếch đại của mạch sử dụng phân cực cố định. Phương pháp này thường được sử dụng trong các mạch khuếch đại tín hiệu nhỏ, nơi mà độ ổn định và tính tuyến tính của tín hiệu là những yếu tố quan trọng.

1. Cấu hình mạch phân cực cố định

Mạch phân cực cố định là một cấu hình cơ bản, trong đó dòng điện một chiều được cung cấp từ nguồn điện qua một điện trở RB, điều chỉnh điểm làm việc của transistor. Điểm làm việc này đảm bảo rằng transistor hoạt động trong vùng tuyến tính, giúp khuếch đại tín hiệu một cách hiệu quả.

2. Xác định các thông số quan trọng

• Điện áp cung cấp \( V_{CC} \)
• Dòng điện cực gốc \( I_B = \frac{V_{CC} - V_{BE}}{R_B} \)
• Dòng điện cực thu \( I_C = \beta \times I_B \)
• Điện áp cực thu \( V_{CE} = V_{CC} - I_C \times R_C \)

3. Phân tích hiệu suất khuếch đại

Hiệu suất khuếch đại của mạch có thể được phân tích dựa trên hệ số khuếch đại điện áp \( A_V \), được tính theo công thức:

\[
A_V = \frac{-\beta \times R_C}{R_B}
\]

Trong đó:

• \( \beta \) là hệ số khuếch đại dòng của transistor
• \( R_C \) là điện trở tải
• \( R_B \) là điện trở phân cực

4. Phân tích độ ổn định

Một trong những thách thức chính của mạch phân cực cố định là độ ổn định kém do sự thay đổi nhiệt độ và thông số của transistor. Để khắc phục, cần sử dụng thêm các biện pháp như hồi tiếp điện áp hoặc sử dụng mạch phân cực bằng bộ chia áp.

5. Kết luận

Mạch phân cực cố định mặc dù đơn giản và dễ thực hiện, nhưng cần chú ý đến vấn đề ổn định để đảm bảo hiệu suất khuếch đại tối ưu. Việc hiểu rõ cách thức hoạt động và các yếu tố ảnh hưởng là chìa khóa để thiết kế mạch khuếch đại hiệu quả.

Trong bài tập này, chúng ta sẽ tính toán độ ổn định nhiệt của một mạch phân cực cho transistor. Để đảm bảo rằng transistor hoạt động ổn định và không bị ảnh hưởng quá nhiều bởi sự thay đổi nhiệt độ, cần phải phân tích các yếu tố liên quan và sử dụng các phương pháp điều chỉnh hợp lý.

Một trong những yếu tố quan trọng ảnh hưởng đến độ ổn định nhiệt là dòng điện phân cực \(I_B\) và điện áp \(V_{CE}\). Chúng ta sẽ đi qua từng bước để phân tích và tính toán các giá trị này.

1. Xác định các giá trị ban đầu:
   • Dòng điện \(I_B\) và \(I_C\).
   • Điện áp \(V_{BE}\) và \(V_{CE}\).
2. Tính toán độ ổn định nhiệt:

   Sử dụng phương trình phân cực cơ bản:

   \[ V_{CE} = V_{CC} - I_C \cdot R_C \]

   Trong đó \(V_{CC}\) là điện áp cung cấp, \(I_C\) là dòng điện qua transistor, và \(R_C\) là điện trở tải.

   Sau đó, tính toán sự thay đổi của \(I_C\) khi nhiệt độ thay đổi, sử dụng hệ số nhiệt của transistor:

   \[ \Delta I_C = \beta \cdot \Delta I_B \]

   Với \(\beta\) là hệ số khuếch đại dòng điện của transistor.

3. Điều chỉnh phân cực để cải thiện độ ổn định:
   • Thêm điện trở hồi tiếp âm để giảm sự phụ thuộc của \(I_C\) vào nhiệt độ.
   • Chọn giá trị điện trở phân cực phù hợp để duy trì độ ổn định nhiệt tốt nhất.

Cuối cùng, kiểm tra lại kết quả bằng cách so sánh các giá trị tính toán với thông số thực tế của transistor và điều chỉnh nếu cần thiết.

Trong bài tập này, chúng ta sẽ thiết kế một mạch khuếch đại sử dụng phân cực bằng cầu chia điện áp. Đây là một phương pháp phổ biến để ổn định điểm làm việc của transistor, giúp đảm bảo rằng transistor hoạt động ổn định bất chấp sự thay đổi của nhiệt độ và sự biến đổi của thông số transistor. Các bước thực hiện như sau:

1. Xác định yêu cầu mạch khuếch đại:
   • Hệ số khuếch đại điện áp \( A_v \) cần đạt được: Ví dụ, \( A_v = 10 \).
   • Dòng điện cực thu \( I_C \): Chọn giá trị \( I_C \) phù hợp, ví dụ \( I_C = 2 \, \text{mA} \).
   • Điện áp cung cấp \( V_{CC} \): Giả sử \( V_{CC} = 12 \, \text{V} \).
2. Tính toán các thông số cơ bản:
   • Tính điện trở tải \( R_C \): \[ R_C = \frac{V_{CC} - V_{CE}}{I_C} \] Giả sử \( V_{CE} = 6 \, \text{V} \), thì: \[ R_C = \frac{12 - 6}{2 \times 10^{-3}} = 3 \, \text{k}\Omega \]
   • Xác định điện trở đầu vào \( R_{in} \) và điện trở ra \( R_{out} \) sao cho phù hợp với mạch tải và nguồn tín hiệu.
3. Thiết kế mạch cầu chia điện áp để phân cực:
   • Lựa chọn giá trị của \( R_1 \) và \( R_2 \) để tạo ra điện áp phân cực \( V_B \): \[ V_B = \frac{R_2}{R_1 + R_2} \times V_{CC} \] Ví dụ, để \( V_B \approx 2 \, \text{V} \), chọn \( R_1 = 47 \, \text{k}\Omega \) và \( R_2 = 10 \, \text{k}\Omega \).
   • Kiểm tra lại giá trị \( V_B \): \[ V_B = \frac{10 \, \text{k}\Omega}{47 \, \text{k}\Omega + 10 \, \text{k}\Omega} \times 12 \, \text{V} \approx 2 \, \text{V} \]
4. Tính toán điện trở \( R_E \) để ổn định phân cực:
   • Sử dụng công thức: \[ V_E = I_E \times R_E \] Chọn \( V_E \approx 10\% V_{CC} = 1.2 \, \text{V} \), khi đó: \[ R_E = \frac{V_E}{I_E} = \frac{1.2 \, \text{V}}{2 \, \text{mA}} = 600 \, \Omega \]
5. Kết nối các thành phần và kiểm tra:
   • Đảm bảo rằng các điện trở \( R_1 \), \( R_2 \), \( R_C \), và \( R_E \) được kết nối chính xác theo sơ đồ mạch.
   • Sử dụng thiết bị đo để kiểm tra các giá trị điện áp và dòng điện trong mạch, đảm bảo rằng điểm làm việc ổn định và hệ số khuếch đại đạt yêu cầu.
6. Thực hiện tối ưu hóa:
   • Điều chỉnh các giá trị điện trở để cải thiện hiệu suất của mạch khuếch đại, nếu cần.
   • Kiểm tra độ ổn định nhiệt và thực hiện các điều chỉnh cần thiết để giảm thiểu sự thay đổi của điểm làm việc do nhiệt độ.

Sau khi hoàn thành các bước trên, bạn sẽ có một mạch khuếch đại sử dụng phân cực bằng cầu chia điện áp với hiệu suất hoạt động ổn định và hệ số khuếch đại như mong muốn.