Công Thức Và Cách Tìm Nguyên Hàm Của Hàm Số Mũ, Hàm Số Logarit

2. Tìm Nguyên Hàm Của Hàm Số Mũ, Logarit

Nguyên hàm của một hàm số được xác định trên đoạn K là hàm số F(x) sao cho F'(x) = f(x) với x thuộc K.

Bạn đang xem: Công Thức Và Cách Tìm Nguyên Hàm Của Hàm Số Mũ, Hàm Số Logarit

2.1. Sử Dụng Các Dạng Nguyên Hàm Cơ Bản

Để tìm nguyên hàm của hàm số mũ hoặc hàm số logarit, chúng ta có thể sử dụng các phép biến đổi đại số. Chúng ta sẽ chuyển biểu thức dưới dấu tích phân về dạng nguyên hàm cơ bản đã được học.

Có bảng nguyên hàm cơ bản như sau:

Bảng công thức nguyên hàm mở rộng:

Ví dụ 1: Tìm nguyên hàm của hàm số sau:

f(x)=$frac{1}{e^{x}-e^{-x}}$

Giải:

Ta có:

$int f(x)dx=int frac{d(e^{x})}{e^{2x-1}}=int frac{d(e^{x})}{e^{2x-1}}=frac{1}{2}lnleft | frac{e^{x}-1}{e^{x}+1} right |+C$

Ví dụ 2: Tìm nguyên hàm của hàm số:

f(x)=$frac{ln(ex)}{3+xlnx}$

Giải:

2.2. Phương Pháp Phân Tích

Học sinh thường sử dụng phương pháp phân tích để tìm nguyên hàm. Đây cũng là một dạng của phương pháp hệ số bất định, nhưng ta sẽ sử dụng các đồng nhất thức quen thuộc.

Chú ý: Nếu bạn gặp khó khăn trong việc chuyển về dạng cơ bản, bạn có thể thực hiện hai bước sau:

1. Thực hiện phép đổi biến t=$e^{x}$, suy ra $dt=e^{x}dx$.

$e^{x}sqrt{e^{2x}-2e^{x}+2}dx=sqrt{t^{2}-2t+2dt}=sqrt{(t-1)^{2}+1dt}$

Lúc này: $int f(x)dx=int sqrt{(t-1)^{2}+1dt}$

2. Thực hiện phép đổi biến u=t-1, suy ra du=dt

Ví dụ 1: Tìm nguyên hàm của hàm số:

Xem thêm : Test IQ bằng hình ảnh và những điều cần lưu ý

f(x)=$frac{1}{1-e^{x}}$

Giải:

Ví dụ 2: Tìm nguyên hàm của hàm số:

f(x)=$e^{x}sqrt{e^{2x}-2e^{x}+2}$

Giải:

2.3. Phương Pháp Đổi Biến

Phương pháp đổi biến được sử dụng cho các hàm logarit và hàm số mũ để chuyển biểu thức dưới dấu tích phân về dạng vô tỉ hoặc hữu tỉ. Để sử dụng phương pháp này trong nguyên hàm của hàm mũ, chúng ta thực hiện các bước sau:

1. Chọn t = φ(x), trong đó φ(x) là hàm số mà ta chọn.
2. Tính vi phân dt = φ'(x)dx.
3. Biểu diễn f(x)dx = g[φ(x)] φ'(x)dx = g(t)dt.
4. Lúc này, I=∫f(x)dx= ∫g(t)dt= G(t) + C.

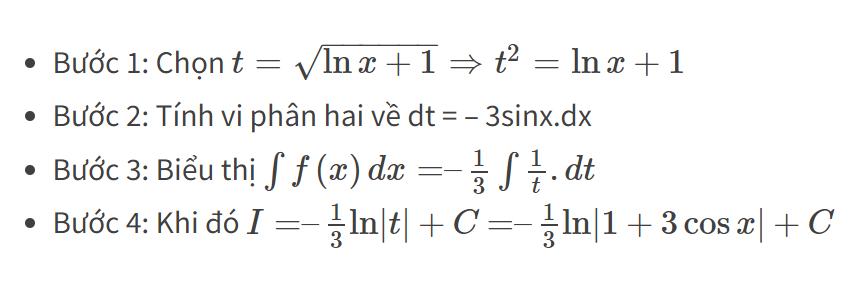
Ví dụ 1: Tìm nguyên hàm của hàm số:

f(x)=$int frac{1}{xsqrt{lnx+1}}dx$

Giải:

Ví dụ 2: Tìm nguyên hàm của hàm số:

f(x)=$frac{1}{1+e^{2x}}$

Giải:

2.4. Phương Pháp Nguyên Hàm Từng Phần

Trong bài toán nguyên hàm hàm số mũ, chúng ta sử dụng phương pháp nguyên hàm từng phần. Điều kiện để áp dụng phương pháp này là hàm số u và v phải liên tục và có đạo hàm liên tục trên đoạn [a,b].

Theo nguyên hàm từng phần, ta có:

$int udv=uv-int vdu$

Ngoài công thức chung như trên, chúng ta còn có thể áp dụng các dạng khác:

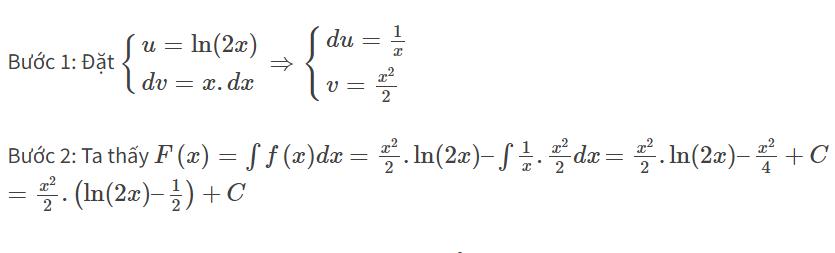
Chú ý: Thứ tự ưu tiên khi đặt u: “Nhất lô, nhì đa, tam lượng, tứ mũ”

Xem thêm : TRƯỜNG TIỂU HỌC NGUYỄN THƯỢNG HIỀN, QUẬN NGÔ QUYỀN, TP HẢI PHÒNG

Ví dụ 1: Tính nguyên hàm của hàm số:

f(x)=$x.e^{2x}$

Giải:

Ví dụ 2: Tính nguyên hàm của hàm số:

f(x)=$int xlnfrac{1-x}{1+x}dx$

Giải:

3. Một Số Bài Tập Tìm Nguyên Hàm Của Hàm Số Mũ Và Logarit (Có Đáp Án)

Nguyên hàm của hàm số mũ có rất nhiều dạng bài tập khác nhau. Hãy cùng xem các ví dụ dưới đây để hiểu rõ hơn và rèn luyện kỹ năng giải toán.

Bài tập 1: Hàm số $(tan^{2}x+tanx+1).e^{x}$ có nguyên hàm là?

Giải:

Bài tập 2: Hàm số: y = $5.7^{x}+x^{2}$ có nguyên hàm là?

Giải:

Bài tập 3: Tìm nguyên hàm F(x) của hàm số y =$3^{x}-5^{x}.F(0)=frac{2}{15}$

Giải:

Bài tập 4: Tìm họ nguyên hàm của hàm số y = $(2x-1)e^{3x}$

Giải:

Bài tập 5: Cho F(x)= $int (2x-1)e^{1-x}dx=(Ax+B).e^{1-x}+C$. Giá trị của T=A+B là bao nhiêu?

Giải

Hy vọng qua bài viết này, các bạn sẽ hiểu rõ về cách tìm nguyên hàm của hàm số mũ và logarit. Hãy truy cập nền tảng học online Vuihoc.vn để ôn tập và nắm chắc hơn về các dạng toán khác nhé! Chúc các bạn ôn thi hiệu quả.

Xem thêm:

• Công thức nguyên hàm Inx và cách giải các dạng bài tập
• Bảng công thức tính nguyên hàm đầy đủ nhất – Toán lớp 12
• Công thức tính nguyên hàm từng phần và bài tập có đáp án
• Phương pháp tính tích phân từng phần và ví dụ minh họa

Nguồn: https://ispacedanang.edu.vn
Danh mục: Học tập