Đạo hàm căn là gì?
Contents
Định nghĩa đạo hàm
Đạo hàm được định nghĩa là tỉ số giữa số gia của hàm số và số gia của một đối số tại một điểm x0. Đạo hàm không chỉ có ý nghĩa hình học mà còn có ý nghĩa vật lý.
Bạn đang xem: Tất tận tật kiến thức về đạo hàm căn: Căn bậc 3, căn u, căn x, căn logarit,…
Đạo hàm căn và định nghĩa của nó
Đạo hàm căn có thể được đơn giản hoá bằng công thức như sau. Cho một hàm số y = f(x) được xác định trên khoảng (a;b) với x0 ∈ (a;b), đạo hàm của hàm số đã cho tại điểm x0 có thể là giới hạn hữu tỉ của tỉ số khi x tiến gần đến x0.
Ký hiệu đạo hàm của căn
Ký hiệu của đạo hàm căn sẽ là f'(x0) hay y'(x0).
Công thức tính đạo hàm căn
Áp dụng công thức tính đạo hàm, ta có công thức tổng quát cho đạo hàm căn: Với hàm số y = căn u, tỉ lệ đạo hàm sẽ là u’/2(căn u). Đây là công thức áp dụng cho hầu hết các bài toán tính đạo hàm của căn.

.png)
Các công thức đạo hàm căn cơ bản
Xem thêm : TÌM HIỂU VỀ BÁC SĨ NHÃN KHOA: OPTICIAN, OPTOMETRIST; OPHTHALMOLOGIST
Đạo hàm căn không phải là một khái niệm đơn giản và nó đòi hỏi sự tìm hiểu và luyện tập đều đặn để nắm vững kiến thức. Dưới đây là một số công thức đạo hàm căn đơn giản mà ai cũng nên biết:
- Đối với căn thức đơn giản, công thức là …
- Công thức tổng quát đạo hàm căn bậc 2 của u, công thức là …
- Đối với các bài toán chứa căn bậc 2 có u dưới mẫu, công thức là …
- Đối với bài toán đạo hàm căn u bậc n, công thức tổng quát là …

Công thức tính chung cho đạo hàm căn thức
Mặc dù có nhiều công thức đạo hàm căn khác nhau, nhưng công thức chung và tổng quát cho đạo hàm căn thức là …
- Đối với đạo hàm căn x bậc n, với n ∈ N*, và n > 1
- Đối với đạo hàm căn u bậc n, với n ∈ N*, và n > 1
Đây là hai công thức bao quát và có thể áp dụng cho nhiều dạng bài toán tính căn khác nhau. Hãy ghi nhớ công thức này.
Một số bài toán cụ thể:
Công tính đạo hàm căn bậc 2
Công thức tổng quát là …
Ví dụ: Tính đạo hàm của hàm số: y = 2(căn x)
Đáp án: A

Công tính đạo hàm căn bậc 3
Công thức tổng quát là …
Đáp án: B
Công tính đạo hàm căn bậc 4
Xem thêm : Công thức, quy tắc tìm x lớp 2, 3, 4, 5 – 6 quy tắc tìm x có ví dụ.
Công thức tổng quát là …
Công tính đạo hàm căn u
Công thức tổng quát là Đối với đạo hàm căn u bậc n, ta có: với n ∈ N*, n > 1
Đáp án: A

Công thức tính đạo hàm căn x
Công thức tổng quát là Đối với đạo hàm căn x bậc n, ta có: với n ∈ N*, n > 1

Đáp án: C
Công thức tính đạo hàm căn logarit
Đối với đạo hàm logarit căn x
Xem thêm : Công thức, quy tắc tìm x lớp 2, 3, 4, 5 – 6 quy tắc tìm x có ví dụ.
Công thức tổng quát là …
Đối với đạo hàm logarit căn u
GIÚP CON HỌC TOÁN KẾT HỢP VỚI TIẾNG ANH SIÊU TIẾT KIỆM CHỈ TRÊN MỘT APP MONKEY MATH. VỚI NỘI DUNG DẠY HỌC ĐA PHƯƠNG PHÁP GIÚP BÉ PHÁT TRIỂN TƯ DUY NÃO BỘ VÀ NGÔN NGỮ TOÀN DIỆN CHỈ VỚI KHOẢNG 2K/NGÀY.

Một số dạng bài tập tự luyện có lời giải
Đạo hàm căn có rất nhiều dạng bài tập đa dạng, đòi hỏi phải hiểu rõ bản chất. Dưới đây là một số dạng bài tập tự luyện phổ biến nhất hiện nay:
Dạng 1: Bài tập tính đạo hàm của những hàm số
Ví dụ: Tính đạo hàm của những hàm số sau
Dạng 2: Bài tập tìm x để theo điều kiện của y’
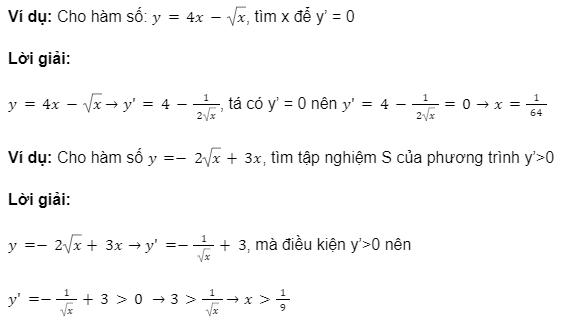

Dạng 3: Tính đạo hàm của hàm số tại một điểm x = a

Một số dạng toán căn cơ bản mà các bạn học sinh nên nắm vững và luyện tập để thực hiện tính toán dễ dàng hơn.

Bài tập đạo hàm căn để học sinh tự luyện

Với những thông tin trên, hy vọng các bạn học sinh đã hiểu được phần nào về đạo hàm căn. Đây là một lĩnh vực kiến thức rộng lớn và yêu cầu sự chăm chỉ rèn luyện. Chúc các bạn học sinh nắm vững và thành thạo kiến thức về đạo hàm căn!
Nguồn: https://ispacedanang.edu.vn
Danh mục: Học tập