Kinh nghiệm học giỏi hình học không gian lớp 11

Hình học không gian lớp 11 có thể là một môn học khá phức tạp. Tuy nhiên, không có gì là không thể nếu có đúng phương pháp và sự kiên nhẫn. Bài viết này sẽ chia sẻ với các bạn những kinh nghiệm học giỏi hình học không gian lớp 11, giúp bạn nắm vững lý thuyết, tưởng tượng và vẽ hình chính xác, và luyện tập hiệu quả. Hãy cùng tìm hiểu nhé!

Bạn đang xem: Kinh nghiệm học giỏi hình học không gian lớp 11

1. Nắm vững lý thuyết bằng việc sử dụng sơ đồ tư duy

Để vẽ hình không gian đúng và chính xác, việc đầu tiên bạn cần làm là học thuộc lý thuyết và nắm rõ các định nghĩa và định lý quan trọng. Tuy nhiên, không chỉ đơn thuần là ghi nhớ, bạn cần biết vận dụng lý thuyết vào bài tập và biến nó thành kĩ năng. Hình học không gian lớp 11 bao gồm rất nhiều bài tập thuộc các chương trình như đường thẳng và mặt phẳng trong không gian, quan hệ song song và vuông góc trong không gian, và nhiều dạng bài tập khác.

Dạng 1: Tìm giao tuyến giữa hai mặt phẳng (P) và (Q)

• Phương pháp 1: Tìm 2 điểm chung của 2 mặt phẳng đó.
• Phương pháp 2: Nếu mặt phẳng (P) và (Q) có chứa hai đường thẳng song song, chỉ cần tìm một điểm chung. Giao tuyến của hai mặt phẳng sẽ là đường thẳng đi qua điểm chung và song song với hai đường thẳng này.

Dạng 2: Tìm giao điểm của đường thẳng (d) và mặt phẳng (α)

Xem thêm : Quy Tắc, Cách Cầm Bút, Cách Viết Nét Chữ Đẹp Thanh Nét Đậm

Phương pháp tổng quát:

• Trường hợp 1: Trong mặt phẳng (α) có sẵn đường thẳng (d’) cắt (d) tại H. Khi đó, giao điểm của (d) và (α) là H.
• Trường hợp 2: Trong mặt phẳng không có sẵn đường thẳng (d1) cắt (d). Khi đó, ta chọn mặt phẳng (β) chứa (d) và cắt (α) theo giao tuyến (d’). Giao điểm của (d’) và (d) là H.

Dạng 3: Chứng minh 3 điểm cùng nằm trên một đường thẳng

Phương pháp: Chứng minh 3 điểm A, B, C thẳng hàng. Ta chứng minh A, B, C cùng thuộc hai mặt phẳng phân biệt.

Dạng 4: Chứng minh 3 đường thẳng đồng quy

Phương pháp 1: Chứng minh giao của hai đường thẳng bất kỳ là điểm chung của hai mặt phẳng mà giao tuyến là đường thẳng thứ ba. Cụ thể:

• Tìm giao điểm của d1 và d2 là H.
• Tìm 2 mặt phẳng (α) và (β) chứa điểm H sao cho: (α) giao (β) là d3.
  Phương pháp 2: Chứng minh d1, d2, d3 không đồng phẳng và cắt nhau từng đôi một.

Dạng 5: Chứng minh đường thẳng d song song với mặt phẳng (α)

Phương pháp 1: Chứng minh d song song với (α) bằng cách chứng minh d // d’, trong đó d’ ⊂ (α).
Phương pháp 2: Chứng minh d nằm trong mặt phẳng khác và song song với mặt phẳng đã cho. Chứng minh d ⊂ (β) sao cho (α) // (β).

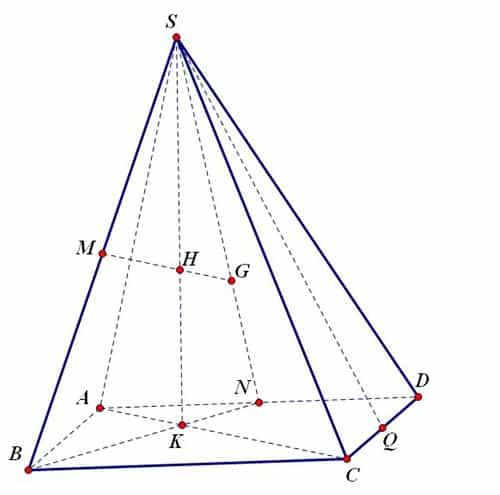
2. Biết cách tưởng tượng và vẽ hình chính xác

Xem thêm : Lộ trình học tiếng Anh chuẩn quốc tế cho học sinh tiểu học

Để vẽ hình, bạn cần đọc kĩ đề bài và nhớ lại kiến thức để áp dụng phù hợp. Tưởng tượng mặt phẳng nào nhìn thấy và mặt phẳng nào không nhìn thấy để sử dụng nét đứt và nét liền cho phù hợp. Hãy dùng bút chì để vẽ trước và sau đó mới sử dụng bút mực để tô lại.

3. Luyện tập thật nhiều

“Cần cù bù thông minh.” Hãy kiên trì và luyện tập thật chăm chỉ để vận dụng kiến thức lý thuyết tốt hơn. Bắt đầu bằng việc vẽ nhiều hình dưới nhiều góc nhìn khác nhau. Nếu gặp khó khăn, hãy nhờ sự giúp đỡ của giáo viên hoặc gia sư toán giỏi để được hướng dẫn ngay.

4. Đầu tư thời gian và tham khảo sách hướng dẫn

Sách giáo khoa và sách bài tập là vũ khí quan trọng để học hình không gian lớp 11. Bên cạnh đó, bạn có thể tham khảo thêm nhiều quyển sách hướng dẫn về các phương pháp giải hình học không gian lớp 11 hoặc tìm kiếm trên mạng để có thêm mẹo vẽ hình sáng tạo và khoa học.

Để trau dồi kỹ năng và phương pháp học hình không gian lớp 11 hiệu quả, hãy liên hệ với chúng tôi để tìm gia sư môn toán dạy kèm tại nhà. Đội ngũ gia sư chuyên môn cao và tận tình của chúng tôi sẽ giúp bạn học tốt hơn.

Nguồn: https://ispacedanang.edu.vn
Danh mục: Học tư duy