Phát Biểu Quy Tắc Momen Lực: Tìm Hiểu Chi Tiết và Ứng Dụng Thực Tế

Quy tắc momen lực là một trong những quy tắc cơ bản trong vật lý học, đặc biệt quan trọng trong cơ học khi nghiên cứu về chuyển động quay. Dưới đây là một số thông tin chi tiết và đầy đủ về quy tắc này.

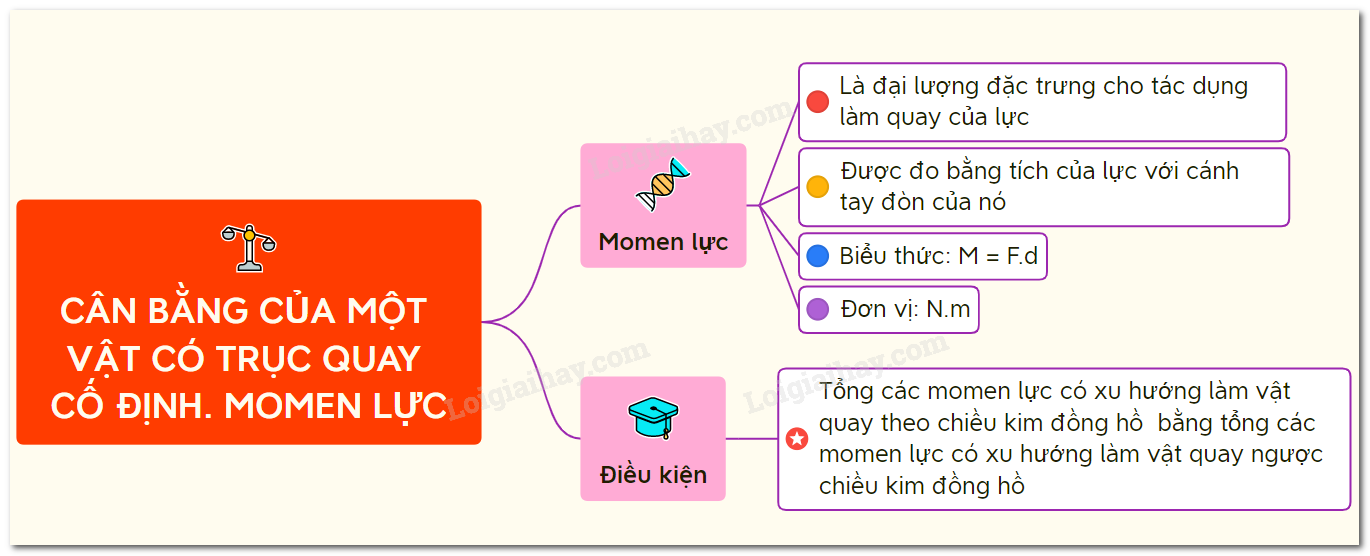
1. Định nghĩa momen lực

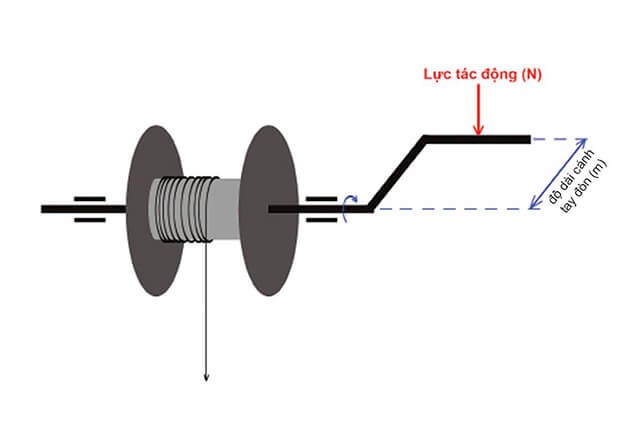
Momen lực là đại lượng đặc trưng cho khả năng làm quay của một lực quanh một trục cố định. Nó được xác định bằng tích của lực tác dụng và khoảng cách từ trục quay đến điểm đặt lực. Công thức tổng quát cho momen lực được biểu diễn như sau:

\( \tau = r \times F \times \sin(\theta) \)

• \(\tau\): Momen lực (N.m)
• \(r\): Khoảng cách từ điểm đặt lực đến trục quay (m)
• \(F\): Lực tác dụng (N)
• \(\theta\): Góc giữa hướng của lực và cánh tay đòn (độ)

2. Quy tắc momen lực

Quy tắc momen lực được phát biểu như sau: Để một vật có trục quay cố định ở trạng thái cân bằng, tổng các momen lực có xu hướng làm vật quay theo chiều kim đồng hồ phải bằng tổng các momen lực có xu hướng làm vật quay ngược chiều kim đồng hồ.

\( \sum \tau_{\text{kim đồng hồ}} = \sum \tau_{\text{ngược chiều kim đồng hồ}} \)

3. Ứng dụng của quy tắc momen lực

Quy tắc momen lực có nhiều ứng dụng trong đời sống và kỹ thuật, bao gồm:

• Kỹ thuật cơ khí: Sử dụng trong thiết kế các công cụ như cờ lê, tua vít, và búa để tăng hiệu quả công việc.
• Xây dựng: Tính toán để đảm bảo an toàn cho các công trình xây dựng như cầu, thang máy, và nhà cao tầng.
• Điều khiển robot: Ứng dụng trong phân tích chuyển động và điều khiển các robot trong công nghiệp.
• Đời sống hàng ngày: Momen lực xuất hiện khi chúng ta mở cửa, xoay ốc vít, hoặc sử dụng các dụng cụ hàng ngày.

4. Ví dụ minh họa về momen lực

Một ví dụ điển hình của momen lực là khi bạn sử dụng cờ lê để vặn một con ốc. Lực tác dụng của tay bạn lên cờ lê tạo ra momen lực giúp xoay con ốc. Momen lực càng lớn, con ốc càng dễ xoay.

5. Bài tập vận dụng

Dưới đây là một số bài tập vận dụng quy tắc momen lực:

1. Một thanh kim loại dài 2m đặt trên một trục quay cố định. Một lực 100N tác dụng vuông góc tại điểm cách trục 1,5m. Tính momen lực tác dụng lên thanh kim loại.
2. Một cánh cửa có bản lề nằm dọc theo một cạnh. Khi tác dụng lực 50N tại tay nắm cách bản lề 0,8m, momen lực là bao nhiêu?

Quy tắc momen lực không chỉ là nền tảng của cơ học mà còn có vai trò quan trọng trong nhiều lĩnh vực kỹ thuật và đời sống hàng ngày. Hiểu biết và ứng dụng đúng quy tắc này sẽ giúp giải quyết nhiều vấn đề thực tiễn một cách hiệu quả.

Momen lực không chỉ là một khái niệm quan trọng trong lý thuyết mà còn có nhiều ứng dụng thực tế trong đời sống và các ngành kỹ thuật. Dưới đây là một số ứng dụng cụ thể của momen lực:

3.1 Ứng dụng trong cơ khí

Momen lực được ứng dụng rộng rãi trong lĩnh vực cơ khí, đặc biệt trong việc thiết kế và sử dụng các công cụ như cờ lê, tua vít, và búa. Những công cụ này sử dụng momen lực để tạo ra lực xoay mạnh mẽ, giúp tháo lắp các ốc vít hoặc bộ phận cơ khí một cách dễ dàng và hiệu quả.

3.2 Ứng dụng trong xây dựng

Trong ngành xây dựng, momen lực được sử dụng để tính toán độ bền và khả năng chịu lực của các công trình như cầu, cột đỡ, và dầm. Các kỹ sư thường tính toán momen lực để đảm bảo rằng các cấu trúc này có thể chịu được các lực tác động mà không bị xoắn hay gãy đổ.

3.3 Ứng dụng trong vật lý học

Trong các thí nghiệm và nghiên cứu vật lý, momen lực được sử dụng để kiểm tra và minh họa các nguyên lý cơ học. Ví dụ, các bài thí nghiệm về đòn bẩy trong trường học thường sử dụng momen lực để giảng dạy về sự cân bằng và nguyên lý bảo toàn momen.

3.4 Ứng dụng trong đời sống hàng ngày

Momen lực cũng xuất hiện trong nhiều hoạt động hàng ngày như mở cửa, xoay tay cầm, hoặc sử dụng các dụng cụ nhà bếp. Ví dụ, khi mở một cánh cửa, lực tác dụng lên tay nắm cửa tạo ra momen lực giúp cửa xoay quanh bản lề.

Nhờ vào sự hiểu biết và ứng dụng momen lực, con người có thể tối ưu hóa thiết kế công cụ, đảm bảo an toàn cho các công trình xây dựng, và giải quyết nhiều vấn đề thực tiễn trong đời sống hàng ngày.

Để củng cố hiểu biết về quy tắc momen lực, chúng ta sẽ cùng giải quyết một số bài tập thực tế. Các bài tập này không chỉ giúp bạn áp dụng lý thuyết mà còn rèn luyện kỹ năng giải quyết vấn đề một cách logic và chính xác.

Bài tập 1: Cân bằng momen lực trên một thanh

Một thanh đồng nhất có chiều dài 2m, khối lượng 10kg, được đặt nằm ngang trên hai điểm tựa A và B. Khoảng cách từ điểm tựa A đến đầu thanh là 0,5m, từ điểm tựa B đến đầu còn lại của thanh là 1,5m. Xác định lực tác dụng lên mỗi điểm tựa để thanh cân bằng.

Hướng dẫn:

• Xác định các lực tác dụng lên thanh, bao gồm trọng lực của thanh và lực tác dụng từ hai điểm tựa.
• Sử dụng quy tắc momen lực để thiết lập phương trình cân bằng.
• Giải phương trình để tìm ra giá trị của các lực tại A và B.

Bài tập 2: Tính momen lực của một cánh cửa

Một cánh cửa có chiều dài 1,2m và khối lượng 15kg được treo trên bản lề. Khi áp dụng một lực 20N vuông góc với cánh cửa tại điểm cách bản lề 1m, hãy tính momen lực và xác định xem cánh cửa có thể xoay hay không.

Hướng dẫn:

• Tính momen lực do trọng lực của cánh cửa.
• Tính momen lực do lực tác dụng bên ngoài.
• So sánh tổng các momen lực để xác định trạng thái của cánh cửa.

Bài tập 3: Momen lực trong cầu treo

Một cầu treo dài 50m, khối lượng 5000kg, được giữ bởi hai cáp treo cách đều ở hai đầu. Nếu trọng lực tác dụng đều lên toàn bộ cầu, hãy tính momen lực tại mỗi điểm neo của cáp treo.

Hướng dẫn:

• Xác định trọng lực tác dụng lên cầu và điểm đặt của lực.
• Sử dụng quy tắc momen lực để thiết lập phương trình cân bằng tại điểm neo.
• Giải phương trình để tìm momen lực tại mỗi cáp treo.

Thông qua các bài tập trên, bạn sẽ nắm vững hơn về cách áp dụng quy tắc momen lực vào các tình huống thực tế khác nhau, từ đơn giản đến phức tạp.