Chủ đề bài tập momen lực có đáp an: Bài viết này cung cấp một tổng hợp đầy đủ các bài tập về momen lực, kèm theo đáp án và lời giải chi tiết. Từ những bài tập cơ bản đến nâng cao, bạn sẽ tìm thấy mọi thứ cần thiết để nắm vững khái niệm và ứng dụng momen lực trong thực tế. Đây là nguồn tài liệu hữu ích cho học sinh và giáo viên.
Mục lục
Bài tập Momen Lực Có Đáp Án
Momen lực là một khái niệm quan trọng trong vật lý, đặc biệt khi nghiên cứu về cân bằng của vật rắn và các hiện tượng liên quan đến lực và chuyển động quay. Dưới đây là một số bài tập momen lực cơ bản kèm đáp án chi tiết để bạn dễ dàng theo dõi và học tập.
1. Bài tập ví dụ về momen lực
Bài tập 1: Một lực tác dụng lên một trục quay với cánh tay đòn dài 1 m. Lực này tạo ra một momen lực 25 N.m. Tính lực tác dụng.
Đáp án:
\[ F = \frac{M}{d} = \frac{25 \, \text{N.m}}{1 \, \text{m}} = 25 \, \text{N} \]
Bài tập 2: Một vật bị tác động bởi lực \( F = 60 \, \text{N} \), tạo ra momen lực 30 N.m. Tính khoảng cách từ trục quay đến điểm đặt lực.
Đáp án:
\[ d = \frac{M}{F} = \frac{30 \, \text{N.m}}{60 \, \text{N}} = 0.5 \, \text{m} \]
Bài tập 3: Lực 80 N tác dụng lên một cánh tay đòn dài 0.5 m. Tính momen lực.
Đáp án:
\[ M = F \times d = 80 \, \text{N} \times 0.5 \, \text{m} = 40 \, \text{N.m} \]
2. Điều kiện cân bằng của vật
Để một vật đạt trạng thái cân bằng, nó phải thỏa mãn hai điều kiện chính:
2.1. Điều kiện cân bằng lực
Tổng hợp lực tác dụng lên vật phải bằng không:
\[ \sum \vec{F} = 0 \]
Điều này có nghĩa là các lực tác dụng lên vật phải tự triệt tiêu lẫn nhau, không gây ra chuyển động thẳng của vật.
2.2. Điều kiện cân bằng momen lực
Tổng hợp momen của các lực tác dụng lên vật phải bằng không:
\[ \sum \vec{M} = 0 \]
Điều này đảm bảo rằng các lực không gây ra chuyển động quay của vật. Momen lực được tính bằng công thức:
\[ \vec{M} = \vec{F} \times \vec{d} \]
Trong đó \( \vec{F} \) là lực tác dụng, và \( \vec{d} \) là cánh tay đòn - khoảng cách vuông góc từ trục quay đến điểm đặt lực.
3. Bài tập tự luận mômen lực
Bài tập 1: Một cánh cửa có chiều rộng 1m, chịu tác dụng của một lực 10N vuông góc với bề mặt cửa tại điểm cách bản lề 0.8m. Tính momen lực tác dụng lên bản lề.
Đáp án:
\[ M = F \times d = 10 \times 0.8 = 8 \, \text{N.m} \]
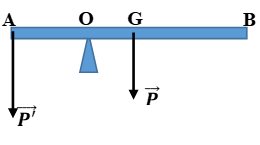
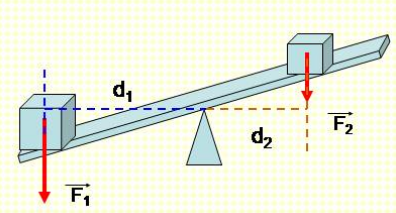
Bài tập 2: Một vật có trọng lượng 100N được treo tại điểm cách điểm tựa của một thanh đòn bẩy 2m. Lực nâng được áp dụng tại đầu kia của thanh cách điểm tựa 3m. Tính lực nâng cần thiết để giữ thanh đòn bẩy cân bằng.
Đáp án:
\[ F_1 \times d_1 = F_2 \times d_2 \]
\[ 100 \times 2 = F_2 \times 3 \]
\[ F_2 = \frac{200}{3} \approx 66.67 \, \text{N} \]
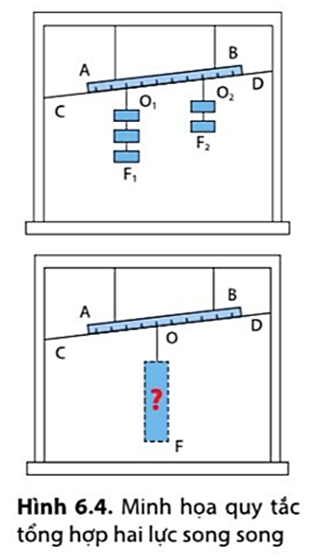
.png)
Tổng Quan Về Momen Lực
Momen lực là một khái niệm quan trọng trong cơ học, biểu thị khả năng của lực làm quay một vật quanh trục cố định. Momen lực được xác định bởi tích của lực tác dụng và khoảng cách từ trục quay đến điểm đặt lực, theo công thức:
\[
\text{Momen Lực} = \text{Lực} \times \text{Khoảng Cách}
\]
Trong đó:
- Lực: Đơn vị tính là Newton (N).
- Khoảng cách: Khoảng cách từ trục quay đến điểm đặt lực, đơn vị tính là mét (m).
Momen lực là yếu tố quyết định trong nhiều bài toán cơ học, từ các bài toán cân bằng cho đến những bài toán liên quan đến chuyển động quay của vật rắn. Hiểu rõ về momen lực giúp bạn giải quyết nhiều tình huống thực tế, chẳng hạn như việc thiết kế cánh tay robot, cơ cấu nâng hạ, hay các bài toán trong xây dựng.
Với mục tiêu nắm vững kiến thức về momen lực, bạn cần thực hành nhiều dạng bài tập khác nhau, từ cơ bản đến nâng cao. Các bài tập thường yêu cầu tính toán momen lực trong các hệ vật rắn, xác định điều kiện cân bằng, và phân tích các yếu tố ảnh hưởng đến momen lực.
Dưới đây là một số bài tập tiêu biểu giúp bạn hiểu rõ hơn về khái niệm này:
- Bài tập tính momen lực đơn giản với một lực duy nhất.
- Bài tập xác định momen lực trong hệ đa lực.
- Bài tập về cân bằng momen lực trong các hệ vật rắn phức tạp.
Nhờ việc giải các bài tập này, bạn sẽ nắm vững khái niệm và ứng dụng của momen lực, từ đó có thể áp dụng vào các tình huống thực tế và nâng cao kỹ năng giải toán của mình.
Các Bài Tập Cơ Bản Về Momen Lực
Các bài tập cơ bản về momen lực giúp bạn hiểu rõ và áp dụng kiến thức lý thuyết vào thực tiễn. Dưới đây là một số dạng bài tập thường gặp, kèm theo hướng dẫn giải chi tiết:
- Bài tập 1: Tính momen lực của một lực tác dụng
Cho một lực \( F = 10 \, \text{N} \) tác dụng vuông góc lên một thanh có chiều dài \( l = 2 \, \text{m} \). Tính momen lực tác dụng lên thanh.
Giải:
\[
M = F \times l = 10 \, \text{N} \times 2 \, \text{m} = 20 \, \text{Nm}
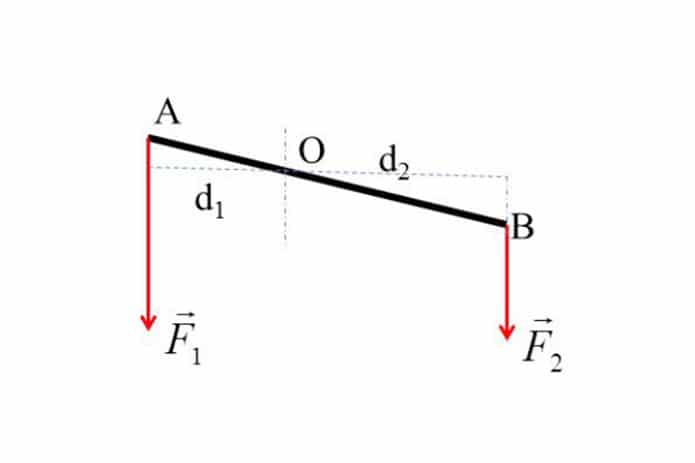
\] - Bài tập 2: Tính momen lực trong hệ hai lực đồng phẳng
Cho hai lực \( F_1 = 5 \, \text{N} \) và \( F_2 = 7 \, \text{N} \) tác dụng lên một thanh có chiều dài \( l = 3 \, \text{m} \) tại các điểm cách nhau 1,5m. Tính tổng momen lực tác dụng lên thanh.
Giải:
\[
M_1 = F_1 \times d_1 = 5 \, \text{N} \times 1,5 \, \text{m} = 7,5 \, \text{Nm}
\]
\[
M_2 = F_2 \times d_2 = 7 \, \text{N} \times 1,5 \, \text{m} = 10,5 \, \text{Nm}
\]Tổng momen lực:
\[
M = M_1 + M_2 = 7,5 \, \text{Nm} + 10,5 \, \text{Nm} = 18 \, \text{Nm}
\] - Bài tập 3: Cân bằng momen lực trong hệ vật rắn
Một thanh dài \( l = 4 \, \text{m} \) có trọng lượng \( P = 40 \, \text{N} \), được treo ngang trên một trục cố định tại điểm cách đầu thanh 1m. Tính lực \( F \) cần thiết tác dụng tại đầu thanh để cân bằng hệ.
Giải:
Để cân bằng, momen lực tại trục cố định phải bằng nhau:
\[
P \times d_1 = F \times d_2
\]Với \( d_1 = 3 \, \text{m} \) và \( d_2 = 1 \, \text{m} \):
\[
40 \, \text{N} \times 3 \, \text{m} = F \times 1 \, \text{m} \Rightarrow F = 120 \, \text{N}
\]
Các bài tập cơ bản này sẽ giúp bạn làm quen với các tính toán liên quan đến momen lực, từ đó chuẩn bị tốt hơn cho những bài tập phức tạp hơn.

Bài Tập Nâng Cao Về Momen Lực
Những bài tập nâng cao về momen lực thường yêu cầu sự kết hợp giữa lý thuyết và kỹ năng tính toán phức tạp. Dưới đây là một số bài tập mẫu giúp bạn rèn luyện và nâng cao khả năng phân tích:
- Bài tập 1: Tính momen lực trong hệ ba lực không đồng phẳng
Ba lực \( F_1 = 8 \, \text{N} \), \( F_2 = 12 \, \text{N} \), và \( F_3 = 15 \, \text{N} \) tác dụng lên một thanh dài \( l = 5 \, \text{m} \) tại các điểm khác nhau trên thanh. Hãy tính tổng momen lực và xác định điều kiện cân bằng của hệ.
Giải:
Giả sử các lực tác dụng tại các điểm cách đầu thanh lần lượt là \( d_1 = 1 \, \text{m} \), \( d_2 = 3 \, \text{m} \), và \( d_3 = 4 \, \text{m} \). Ta có:
\[
M_1 = F_1 \times d_1 = 8 \, \text{N} \times 1 \, \text{m} = 8 \, \text{Nm}
\]
\[
M_2 = F_2 \times d_2 = 12 \, \text{N} \times 3 \, \text{m} = 36 \, \text{Nm}
\]
\[
M_3 = F_3 \times d_3 = 15 \, \text{N} \times 4 \, \text{m} = 60 \, \text{Nm}
\]Tổng momen lực:
\[
M = M_1 + M_2 + M_3 = 8 \, \text{Nm} + 36 \, \text{Nm} + 60 \, \text{Nm} = 104 \, \text{Nm}
\] - Bài tập 2: Xác định momen lực trong hệ vật rắn chịu tác động của lực không song song
Một thanh rắn có chiều dài \( l = 6 \, \text{m} \) chịu tác động của hai lực không song song \( F_1 = 10 \, \text{N} \) và \( F_2 = 14 \, \text{N} \) tác dụng tại các điểm khác nhau trên thanh. Hãy xác định tổng momen lực tác dụng lên thanh và vị trí cân bằng của thanh.
Giải:
Giả sử các lực tác dụng tại các điểm cách đầu thanh lần lượt là \( d_1 = 2 \, \text{m} \) và \( d_2 = 5 \, \text{m} \). Ta có:
\[
M_1 = F_1 \times d_1 = 10 \, \text{N} \times 2 \, \text{m} = 20 \, \text{Nm}
\]
\[
M_2 = F_2 \times d_2 = 14 \, \text{N} \times 5 \, \text{m} = 70 \, \text{Nm}
\]Tổng momen lực:
\[
M = M_1 + M_2 = 20 \, \text{Nm} + 70 \, \text{Nm} = 90 \, \text{Nm}
\]Vị trí cân bằng của thanh sẽ là điểm mà tổng momen lực tại đó bằng không, đòi hỏi việc áp dụng thêm lý thuyết và phương pháp phân tích nâng cao.
- Bài tập 3: Phân tích momen lực trong hệ đa lực có sự thay đổi vị trí tác dụng
Hệ gồm ba lực tác dụng lên một đòn bẩy tại các vị trí khác nhau. Lực \( F_1 \), \( F_2 \), và \( F_3 \) lần lượt là 5N, 10N, và 7N tác động tại các điểm khác nhau. Xác định sự thay đổi của tổng momen lực khi vị trí tác dụng của \( F_2 \) thay đổi dọc theo thanh.
Giải:
Giả sử các lực ban đầu tác dụng tại các điểm cách đầu thanh lần lượt là \( d_1 = 1 \, \text{m} \), \( d_2 = 4 \, \text{m} \), và \( d_3 = 6 \, \text{m} \). Ta có:
\[
M_1 = F_1 \times d_1 = 5 \, \text{N} \times 1 \, \text{m} = 5 \, \text{Nm}
\]
\[
M_2 = F_2 \times d_2 = 10 \, \text{N} \times 4 \, \text{m} = 40 \, \text{Nm}
\]
\[
M_3 = F_3 \times d_3 = 7 \, \text{N} \times 6 \, \text{m} = 42 \, \text{Nm}
\]Khi vị trí tác dụng của \( F_2 \) thay đổi, giá trị của \( d_2 \) thay đổi, kéo theo sự thay đổi của momen lực \( M_2 \). Bài toán này đòi hỏi phân tích chi tiết sự ảnh hưởng của từng yếu tố đến hệ và khả năng cân bằng của hệ.
Các bài tập nâng cao này yêu cầu sự kết hợp của nhiều khái niệm vật lý và kỹ năng phân tích, giúp bạn nắm vững lý thuyết và ứng dụng vào thực tế.

XEM THÊM:
Lời Giải Chi Tiết Cho Các Bài Tập Momen Lực
Dưới đây là các bước giải chi tiết cho một số bài tập momen lực cơ bản và nâng cao. Các bài tập này giúp bạn rèn luyện khả năng tính toán và áp dụng công thức momen lực vào các tình huống khác nhau.
Bài Tập 1: Tính Momen Lực
Một lực 10 N tác dụng lên một thanh ở khoảng cách 2 m từ trục quay. Hãy tính momen lực.
- Xác định các yếu tố liên quan:
- Lực tác dụng: \( F = 10 \, \text{N} \)
- Khoảng cách từ điểm tác dụng lực đến trục quay: \( d = 2 \, \text{m} \)
- Áp dụng công thức tính momen lực: \[ M = F \times d = 10 \, \text{N} \times 2 \, \text{m} = 20 \, \text{N.m} \]
- Kết luận: Momen lực là 20 N·m.
Bài Tập 2: Vật Nặng Treo Trên Thanh
Một vật nặng 5 kg treo ở đầu một thanh dài 3 m, thanh được giữ cố định ở đầu kia. Hãy tính momen lực tác dụng lên điểm giữ cố định (giả sử trọng lực là 9,8 m/s²).
- Tính lực tác dụng do trọng lực: \[ F = 5 \, \text{kg} \times 9,8 \, \text{m/s}^2 = 49 \, \text{N} \]
- Tính momen lực tác dụng lên điểm giữ cố định: \[ M = F \times d = 49 \, \text{N} \times 3 \, \text{m} = 147 \, \text{N.m} \]
- Kết luận: Momen lực tác dụng lên điểm giữ cố định là 147 N·m.
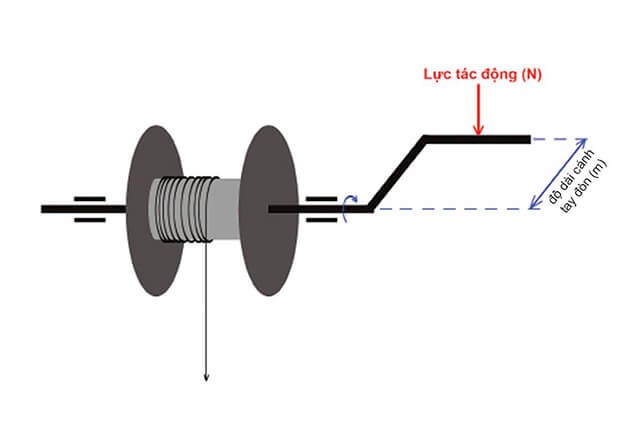
Bài Tập 3: Momen Lực Khi Vặn Ốc
Một người dùng một cái cờ lê dài 0,5 m để vặn một con ốc với lực 100 N. Hãy tính momen lực tác dụng lên con ốc.
- Xác định các yếu tố liên quan:
- Lực tác dụng: \( F = 100 \, \text{N} \)
- Chiều dài cờ lê: \( d = 0,5 \, \text{m} \)
- Áp dụng công thức tính momen lực: \[ M = F \times d = 100 \, \text{N} \times 0,5 \, \text{m} = 50 \, \text{N.m} \]
- Kết luận: Momen lực tác dụng lên con ốc là 50 N·m.
Kết Luận
Các bài tập trên giúp bạn nắm vững cách tính momen lực thông qua các tình huống thực tế. Hãy luyện tập thêm để cải thiện kỹ năng và áp dụng một cách chính xác các công thức trong các bài toán khác nhau.

Bài Tập Momen Lực Trong Thực Tế
Momen lực không chỉ là một khái niệm lý thuyết, mà còn được ứng dụng rộng rãi trong đời sống hàng ngày và công việc thực tế. Dưới đây là một số ví dụ bài tập momen lực liên quan đến các tình huống thực tế để giúp bạn hiểu rõ hơn về cách áp dụng kiến thức này.
Bài Tập 1: Momen Lực Khi Mở Cửa
Khi bạn mở một cánh cửa, lực mà bạn tác dụng vào tay nắm cửa tạo ra momen lực quanh bản lề. Giả sử bạn tác dụng lực 30 N vào tay nắm cửa cách bản lề 0,8 m, hãy tính momen lực.
- Xác định các yếu tố liên quan:
- Lực tác dụng: \( F = 30 \, \text{N} \)
- Khoảng cách từ điểm tác dụng lực đến trục quay: \( d = 0,8 \, \text{m} \)
- Áp dụng công thức tính momen lực: \[ M = F \times d = 30 \, \text{N} \times 0,8 \, \text{m} = 24 \, \text{N.m} \]
- Kết luận: Momen lực tạo ra khi mở cửa là 24 N·m.
Bài Tập 2: Momen Lực Trên Xà Đơn
Một người nặng 70 kg đu xà đơn, khoảng cách từ tay đến xà là 0,5 m. Hãy tính momen lực mà người đó tạo ra quanh trục quay là điểm giữ xà đơn (giả sử trọng lực là 9,8 m/s²).
- Tính lực tác dụng do trọng lực: \[ F = 70 \, \text{kg} \times 9,8 \, \text{m/s}^2 = 686 \, \text{N} \]
- Tính momen lực tác dụng lên trục quay: \[ M = F \times d = 686 \, \text{N} \times 0,5 \, \text{m} = 343 \, \text{N.m} \]
- Kết luận: Momen lực tác dụng lên trục quay của xà đơn là 343 N·m.
Bài Tập 3: Momen Lực Khi Dùng Cờ Lê
Một kỹ sư sử dụng một cờ lê dài 1,2 m để vặn một bu lông với lực 50 N. Hãy tính momen lực tác dụng lên bu lông.
- Xác định các yếu tố liên quan:
- Lực tác dụng: \( F = 50 \, \text{N} \)
- Chiều dài cờ lê: \( d = 1,2 \, \text{m} \)
- Áp dụng công thức tính momen lực: \[ M = F \times d = 50 \, \text{N} \times 1,2 \, \text{m} = 60 \, \text{N.m} \]
- Kết luận: Momen lực tác dụng lên bu lông là 60 N·m.
Kết Luận
Các bài tập trên minh họa rõ ràng momen lực trong thực tế. Những bài tập này không chỉ giúp bạn hiểu sâu hơn về lý thuyết, mà còn rèn luyện khả năng ứng dụng kiến thức vào cuộc sống hàng ngày.
Các Lưu Ý Khi Làm Bài Tập Momen Lực
Khi làm bài tập về momen lực, có một số lưu ý quan trọng mà bạn cần nắm rõ để đảm bảo việc giải bài tập được chính xác và hiệu quả. Dưới đây là các lưu ý chi tiết:
1. Lưu Ý Về Đơn Vị Đo Lực Và Khoảng Cách
- Sử dụng đúng đơn vị: Momen lực thường được tính bằng Newton mét (N.m). Đảm bảo lực (F) được đo bằng Newton (N) và khoảng cách (d) được đo bằng mét (m).
- Kiểm tra chuyển đổi đơn vị: Nếu bài tập cho dữ liệu với các đơn vị khác nhau (ví dụ: cm, mm), bạn cần chuyển đổi về cùng đơn vị chuẩn trước khi tính toán.
2. Lưu Ý Về Sử Dụng Công Thức Momen Lực
- Hiểu công thức cơ bản: Công thức tính momen lực là \( M = F \times d \), trong đó M là momen lực, F là lực tác dụng, và d là khoảng cách từ trục quay đến điểm đặt lực.
- Xác định đúng điểm đặt lực: Điểm đặt lực là vị trí trên vật mà lực tác dụng, điều này ảnh hưởng trực tiếp đến giá trị momen lực.
- Phân tích vector lực: Đảm bảo rằng lực F được tính theo hướng vuông góc với cánh tay đòn để đạt kết quả chính xác nhất.
3. Lưu Ý Về Phân Tích Bài Toán Momen Lực
- Xác định hệ lực: Khi có nhiều lực tác dụng lên vật, bạn cần tính toán từng momen lực riêng lẻ và tổng hợp chúng để xác định tổng momen.
- Xem xét điều kiện cân bằng: Để vật cân bằng, tổng momen tác dụng lên vật phải bằng không (\( \sum M = 0 \)). Điều này rất quan trọng khi giải các bài toán về cân bằng vật rắn.
- Sơ đồ lực: Vẽ sơ đồ lực và momen sẽ giúp bạn hình dung rõ ràng các lực và momen đang tác dụng lên vật, từ đó phân tích chính xác hơn.
Bằng cách tuân thủ các lưu ý trên, bạn sẽ nắm vững kỹ năng giải bài tập về momen lực, từ những bài cơ bản đến những bài nâng cao. Luôn cẩn thận trong việc phân tích và tính toán để đạt được kết quả tốt nhất.