Vật lý 10 Momen lực: Khái niệm, Công thức và Ứng dụng Thực tế

Trong chương trình Vật lý lớp 10, momen lực là một khái niệm quan trọng được sử dụng để mô tả tác dụng quay của một lực đối với một vật có trục quay cố định. Dưới đây là tổng hợp chi tiết về momen lực và quy tắc liên quan.

1. Định nghĩa momen lực

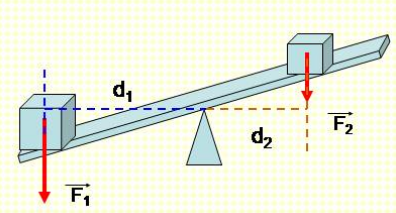
Momen lực là đại lượng đặc trưng cho tác dụng làm quay của một lực đối với một trục quay. Nó được xác định bằng tích của lực với cánh tay đòn của nó:

$$M = F \cdot d$$

Trong đó:

• M: Momen lực (đơn vị: N.m)
• F: Lực tác dụng (đơn vị: N)
• d: Cánh tay đòn - khoảng cách từ trục quay đến đường thẳng mang lực (đơn vị: m)

2. Quy tắc momen lực

Để một vật rắn có trục quay cố định nằm cân bằng, tổng các momen lực có xu hướng làm vật quay theo chiều kim đồng hồ phải bằng tổng các momen lực có xu hướng làm vật quay ngược chiều kim đồng hồ:

$$\sum M_{\text{thuận}} = \sum M_{\text{nghịch}}$$

3. Thí nghiệm và ứng dụng thực tế

Momen lực không chỉ là lý thuyết mà còn được kiểm chứng qua nhiều thí nghiệm thực tế và ứng dụng trong đời sống:

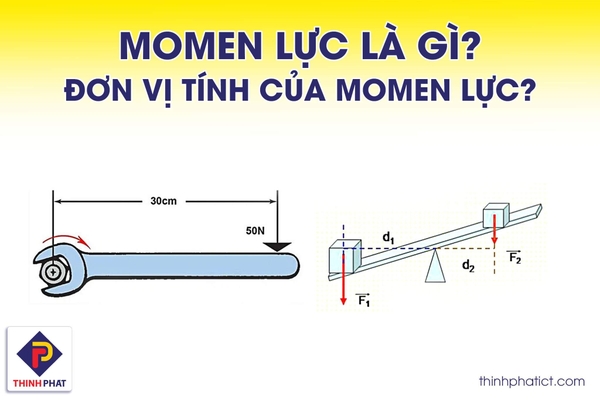
• Trong cơ khí, các công cụ như cờ lê được thiết kế để có cánh tay đòn dài, giúp tăng momen lực và dễ dàng siết hoặc nới lỏng ốc vít.
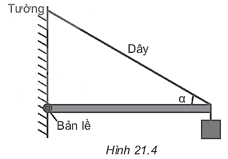
• Khi mở cửa, tay nắm cửa thường được đặt xa bản lề để tăng momen lực, giúp mở cửa dễ dàng hơn.

4. Bài tập ví dụ

Dưới đây là một bài tập minh họa cách tính momen lực:

1. Một thanh sắt có trọng lượng 200N, chiều dài 7,5m, được đặt trên một trục quay cách đầu A của thanh 2,5m. Phải tác dụng một lực bao nhiêu tại đầu B để thanh nằm cân bằng?

Để giải bài tập này, ta áp dụng quy tắc momen lực và các công thức đã học.

5. Lưu ý khi học về momen lực

• Momen lực phụ thuộc vào cả độ lớn của lực và khoảng cách từ lực đến trục quay.
• Trong một số trường hợp, vật không có trục quay cố định cũng có thể áp dụng quy tắc momen lực nếu xuất hiện trục quay trong tình huống cụ thể.

Momen lực là một khái niệm quan trọng trong Vật lý, đặc biệt là trong chương trình Vật lý lớp 10. Nó giúp chúng ta hiểu cách một lực có thể gây ra chuyển động quay quanh một điểm hay trục quay. Momen lực được sử dụng để phân tích và giải thích nhiều hiện tượng vật lý trong cuộc sống hàng ngày cũng như trong các ứng dụng kỹ thuật.

Momen lực được định nghĩa bằng tích của lực tác dụng lên vật và khoảng cách từ điểm đặt lực đến trục quay. Biểu thức tính momen lực được biểu diễn dưới dạng:

$$M = F \cdot d$$

Trong đó:

• M: Momen lực (đơn vị: N.m)
• F: Lực tác dụng (đơn vị: N)
• d: Cánh tay đòn - khoảng cách từ trục quay đến đường thẳng mang lực (đơn vị: m)

Momen lực đóng vai trò quan trọng trong việc giữ cân bằng cho các vật thể, chẳng hạn như khi mở cửa hoặc khi sử dụng các công cụ như cờ lê. Hiểu được momen lực giúp chúng ta áp dụng hiệu quả hơn các nguyên lý vật lý trong đời sống và kỹ thuật.

Thí nghiệm về momen lực giúp học sinh hiểu rõ hơn về nguyên lý và cách tính toán momen lực thông qua quan sát trực quan và thực hành. Dưới đây là hướng dẫn chi tiết về cách thực hiện một thí nghiệm cơ bản để minh họa momen lực.

Dụng cụ thí nghiệm:

• Một thanh ngang đồng chất (có chiều dài và trọng lượng biết trước).
• Một giá đỡ để thanh có thể xoay quanh trục cố định.
• Quả cân với các khối lượng khác nhau.
• Thước đo để đo khoảng cách từ trục quay đến điểm đặt lực.
• Dây treo để gắn quả cân lên thanh.

Cách thực hiện thí nghiệm:

1. Đặt thanh ngang lên giá đỡ sao cho nó có thể xoay quanh trục cố định ở giữa thanh.
2. Treo một quả cân tại một điểm bất kỳ trên thanh, đo khoảng cách từ điểm đó đến trục quay (gọi là cánh tay đòn).
3. Ghi lại giá trị lực (trọng lượng của quả cân) và cánh tay đòn.
4. Tính momen lực tạo ra bởi quả cân theo công thức: M = F \cdot d.
5. Lặp lại thí nghiệm với các vị trí khác nhau của quả cân hoặc với các khối lượng khác nhau.
6. Quan sát sự thay đổi trong trạng thái cân bằng của thanh khi thay đổi momen lực. Điều chỉnh vị trí hoặc khối lượng sao cho tổng các momen lực theo chiều kim đồng hồ bằng tổng các momen lực ngược chiều kim đồng hồ.

Kết quả và nhận xét:

Qua thí nghiệm, học sinh có thể thấy rằng momen lực phụ thuộc vào cả lực tác dụng và cánh tay đòn. Khi tổng momen lực theo hai chiều bằng nhau, thanh sẽ nằm cân bằng. Thí nghiệm này giúp minh họa một cách trực quan và thực tế về cách momen lực hoạt động, củng cố kiến thức lý thuyết đã học trong lớp.

Momen lực là một khái niệm không chỉ tồn tại trong lý thuyết, mà còn có rất nhiều ứng dụng thực tế trong đời sống hàng ngày và trong các ngành công nghiệp khác nhau. Dưới đây là một số ví dụ cụ thể về cách momen lực được áp dụng.

• 1. Cờ lê và công cụ siết ốc vít: Momen lực được sử dụng khi bạn sử dụng cờ lê để siết hoặc mở các đai ốc. Khi tăng chiều dài của cờ lê, bạn đang tăng cánh tay đòn, từ đó tăng momen lực, giúp dễ dàng hơn trong việc xoay đai ốc mà không cần phải dùng quá nhiều lực.
• 2. Cửa ra vào: Tay nắm cửa thường được đặt cách xa bản lề để tăng cánh tay đòn, giúp việc mở cửa trở nên dễ dàng hơn. Nếu tay nắm cửa đặt quá gần bản lề, momen lực sẽ giảm và bạn sẽ cần nhiều lực hơn để mở cửa.
• 3. Bập bênh: Trò chơi bập bênh là một ứng dụng rõ ràng của momen lực. Khi hai người có khối lượng khác nhau chơi bập bênh, người nặng hơn có thể ngồi gần trục quay hơn để đạt được cân bằng, nhờ điều chỉnh cánh tay đòn của momen lực.
• 4. Cần trục và cần cẩu: Trong công nghiệp xây dựng, cần trục và cần cẩu sử dụng momen lực để nâng các vật nặng. Chiều dài của cần trục ảnh hưởng lớn đến khả năng nâng vật của nó. Càng dài cánh tay của cần trục, momen lực càng lớn và nó có thể nâng được vật nặng hơn.
• 5. Máy quay phim và camera: Trong việc điều chỉnh độ nghiêng của máy quay phim, momen lực được sử dụng để giữ cho máy ổn định. Khi điều chỉnh các góc quay, momen lực giúp đảm bảo rằng máy quay không bị nghiêng hoặc lật, giữ cho hình ảnh ổn định.

Như vậy, momen lực không chỉ là một khái niệm trừu tượng trong Vật lý mà còn đóng vai trò thiết yếu trong nhiều hoạt động thực tế, từ những công việc đơn giản hàng ngày đến các ứng dụng công nghệ phức tạp.

Việc thực hành qua các bài tập giúp học sinh củng cố kiến thức về momen lực, hiểu rõ hơn về cách áp dụng lý thuyết vào giải quyết các tình huống thực tế. Dưới đây là một số bài tập vận dụng cụ thể mà bạn có thể thực hành.

1. Bài tập 1: Tính momen lực cơ bản

   Một lực \( F = 20 \, N \) tác dụng vuông góc lên một thanh dài \( 2 \, m \) tại điểm cách trục quay \( 1.5 \, m \). Hãy tính momen lực mà lực này tạo ra đối với trục quay.

   Giải:

   • Sử dụng công thức: \( M = F \cdot d \)
   • Thay giá trị: \( M = 20 \, N \cdot 1.5 \, m = 30 \, N \cdot m \)
   • Kết luận: Momen lực tạo ra là \( 30 \, N \cdot m \).
2. Bài tập 2: Cân bằng momen lực

   Một thanh ngang dài \( 4 \, m \) có trọng lượng không đáng kể, được đặt cân bằng trên một điểm tựa. Trên thanh có hai quả cân đặt tại hai đầu. Quả cân thứ nhất có khối lượng \( 10 \, kg \) được đặt cách điểm tựa \( 1 \, m \), quả cân thứ hai có khối lượng \( 5 \, kg \) được đặt cách điểm tựa bao nhiêu để thanh nằm cân bằng?

   Giải:

   • Gọi khoảng cách từ quả cân thứ hai đến điểm tựa là \( d \).
   • Sử dụng quy tắc cân bằng momen lực: \( M_1 = M_2 \)
   • Áp dụng: \( 10 \, kg \cdot 9.8 \, m/s^2 \cdot 1 \, m = 5 \, kg \cdot 9.8 \, m/s^2 \cdot d \)
   • Kết quả: \( d = 2 \, m \)
3. Bài tập 3: Ứng dụng momen lực trong đời sống

   Hãy tính lực cần thiết để mở một cửa xoay có chiều dài cánh cửa là \( 0.8 \, m \) nếu biết rằng momen lực cần thiết để mở cửa là \( 12 \, N \cdot m \).

   Giải:

   • Sử dụng công thức: \( F = \frac{M}{d} \)
   • Thay giá trị: \( F = \frac{12 \, N \cdot m}{0.8 \, m} = 15 \, N \)
   • Kết luận: Lực cần thiết để mở cửa là \( 15 \, N \).

Những bài tập trên giúp học sinh hiểu rõ hơn về ứng dụng của momen lực trong các tình huống thực tế và cách tính toán liên quan.

Học về momen lực không chỉ đòi hỏi sự hiểu biết lý thuyết mà còn cần khả năng áp dụng vào thực tế. Dưới đây là một số lưu ý quan trọng mà bạn nên ghi nhớ:

6.1 Các lỗi thường gặp khi giải bài tập

• Nhầm lẫn giữa cánh tay đòn và lực: Nhiều học sinh thường nhầm lẫn giữa cánh tay đòn (khoảng cách từ trục quay đến giá của lực) và lực tác dụng. Hãy nhớ rằng momen lực được tính bằng tích của lực và cánh tay đòn theo công thức: \( M = F \times d \), với \( d \) là khoảng cách vuông góc từ trục quay đến giá của lực.
• Không chú ý đến đơn vị: Đảm bảo rằng bạn luôn sử dụng đúng đơn vị trong các bài tập. Đặc biệt, đơn vị của momen lực thường là N.m (Newton mét), không nhầm với các đơn vị khác.
• Quên xét chiều của momen lực: Momen lực có thể quay theo chiều kim đồng hồ hoặc ngược chiều kim đồng hồ. Khi giải bài tập, đừng quên xét chiều của momen để đảm bảo tính toán chính xác.

6.2 Mẹo ghi nhớ công thức và quy tắc

• Liên tưởng với thực tế: Để dễ nhớ công thức, bạn có thể liên tưởng momen lực như việc sử dụng một cái đòn bẩy. Lực tác dụng càng lớn và cánh tay đòn càng dài thì momen lực càng lớn.
• Thực hành với các bài tập đa dạng: Để nắm vững quy tắc momen lực, hãy thực hành với nhiều dạng bài tập khác nhau, từ đơn giản đến phức tạp. Việc này sẽ giúp bạn không chỉ nhớ lý thuyết mà còn biết cách áp dụng một cách linh hoạt.
• Sử dụng sơ đồ tư duy: Vẽ sơ đồ tư duy để hệ thống hóa kiến thức về momen lực. Điều này sẽ giúp bạn nhìn nhận lại toàn bộ nội dung một cách trực quan và dễ nhớ hơn.