Bài Tập Quy Tắc Momen Lực: Hướng Dẫn Chi Tiết Và Ví Dụ Thực Tế

Quy tắc momen lực là một chủ đề quan trọng trong môn Vật lý, đặc biệt trong các chương trình học từ lớp 10 trở lên. Dưới đây là tổng hợp các thông tin chi tiết và đầy đủ nhất về bài tập quy tắc momen lực, cùng với các ví dụ minh họa và hướng dẫn giải chi tiết.

1. Khái Niệm Momen Lực

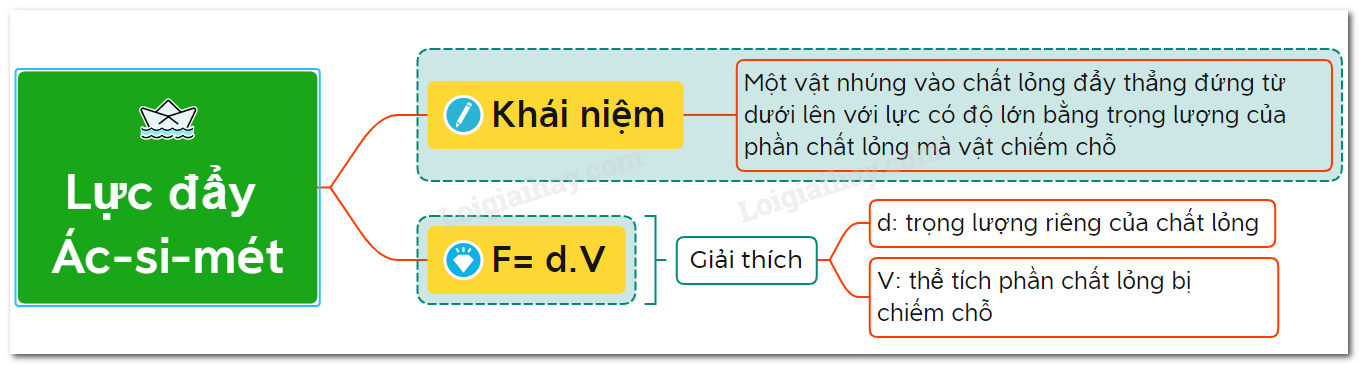
Momen lực (ký hiệu là M) là đại lượng đặc trưng cho tác dụng làm quay của lực đối với một trục quay. Công thức tính momen lực được xác định như sau:

\( M = F \times d \)

Trong đó:

• M: Momen lực (đơn vị: Nm)
• F: Lực tác dụng (đơn vị: N)
• d: Khoảng cách từ điểm đặt lực đến trục quay (cánh tay đòn) (đơn vị: m)

2. Định Luật Về Momen Lực

Định luật cân bằng momen lực phát biểu rằng: Để một vật thể ở trạng thái cân bằng quay, tổng momen lực tác dụng lên nó phải bằng không.

\( \sum M = 0 \)

Điều này có nghĩa là momen lực theo chiều kim đồng hồ phải bằng momen lực theo chiều ngược kim đồng hồ.

3. Các Dạng Bài Tập Momen Lực

Các bài tập về momen lực thường được chia thành nhiều dạng khác nhau, từ cơ bản đến nâng cao. Dưới đây là một số dạng bài tập phổ biến:

1. Bài tập tính momen lực đơn giản: Tính momen lực khi biết lực tác dụng và khoảng cách từ điểm đặt lực đến trục quay.
2. Bài tập cân bằng của vật rắn: Xác định các lực tác dụng lên vật và sử dụng quy tắc momen lực để tìm điều kiện cân bằng.
3. Bài tập về ngẫu lực: Tính momen của ngẫu lực tác dụng lên một vật và xác định điều kiện cân bằng của vật đó.

4. Ví Dụ Minh Họa

Để hiểu rõ hơn về quy tắc momen lực, hãy xem xét các ví dụ minh họa sau:

Ví Dụ 1: Tính Momen Lực Đơn Giản

Một thanh ngang dài 1.5 mét, có lực 10 N tác dụng vuông góc tại điểm cách trục quay 1 mét. Tính momen lực tác dụng lên thanh.

\( M = F \times d = 10 \times 1 = 10 \, \text{Nm} \)

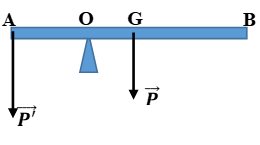
Ví Dụ 2: Bài Tập Về Cân Bằng Vật Rắn

Một cái thước AB dài 2 mét đặt trên mặt bàn, có trục quay tại điểm O cách đầu A một khoảng 80 cm. Lực F tác dụng lên đầu A theo phương vuông góc với thước. Xác định điều kiện để thước cân bằng.

Sử dụng quy tắc momen lực:

\( M_{\text{A}} = M_{\text{B}} \)

Ta có thể tính toán và xác định vị trí tác dụng lực để thước nằm cân bằng.

5. Ứng Dụng Thực Tiễn Của Momen Lực

Momen lực có nhiều ứng dụng thực tiễn trong cuộc sống và kỹ thuật, như:

• Thiết kế các công cụ và máy móc để đảm bảo hoạt động hiệu quả.
• Phân tích và xây dựng các công trình kỹ thuật và kiến trúc.
• Đảm bảo an toàn trong các phương tiện giao thông.

6. Bài Tập Tự Luyện

Dưới đây là một số bài tập tự luyện để bạn ôn tập và nắm vững quy tắc momen lực:

• Bài tập 1: Một lực có độ lớn 15 N tác dụng lên một vật rắn quay quanh trục cố định, với khoảng cách từ giá của lực đến trục quay là 0.5 mét. Tính momen lực.
• Bài tập 2: Xác định điều kiện cân bằng của một thanh đồng chất dài 2 mét, chịu tác dụng của hai lực không song song.
• Bài tập 3: Tính momen ngẫu lực trong một hệ hai lực song song, ngược chiều, bằng nhau về độ lớn.

Quy tắc momen lực là một trong những nguyên lý cơ bản trong vật lý học, đặc biệt quan trọng trong việc giải thích và phân tích các chuyển động quay của vật thể. Nó cho phép chúng ta hiểu rõ hơn về cách mà các lực tác dụng lên một vật có thể gây ra chuyển động quay quanh một trục cố định. Momen lực, hay còn gọi là lực quay, được định nghĩa là tích của lực tác dụng và khoảng cách từ điểm đặt lực đến trục quay.

Công thức tính momen lực cơ bản là:

$$ M = F \times d $$

Trong đó:

• M là momen lực
• F là lực tác dụng
• d là khoảng cách từ điểm đặt lực đến trục quay (còn gọi là cánh tay đòn)

Nếu lực không vuông góc với cánh tay đòn, công thức được điều chỉnh như sau:

$$ M = F \times d \times \sin(\theta) $$

Trong đó, \( \theta \) là góc giữa lực và cánh tay đòn.

Định luật cân bằng momen lực phát biểu rằng: Để một vật thể ở trạng thái cân bằng quay, tổng momen lực tác dụng lên nó phải bằng không, tức là:

$$ \sum M = 0 $$

Hiểu rõ quy tắc momen lực giúp chúng ta ứng dụng vào nhiều lĩnh vực thực tiễn như thiết kế công cụ, phân tích kết cấu trong xây dựng và đánh giá độ ổn định của các phương tiện giao thông.

Quy tắc momen lực không chỉ là một khái niệm lý thuyết mà còn có ứng dụng rộng rãi trong nhiều bài tập thực tiễn. Dưới đây là các dạng bài tập cơ bản và nâng cao về quy tắc momen lực, giúp bạn hiểu rõ hơn và ứng dụng linh hoạt trong các bài toán vật lý.

1. 2.1. Bài Tập Tính Momen Lực Đơn Giản

   Đây là dạng bài tập cơ bản nhất, yêu cầu tính momen lực khi biết lực tác dụng \( F \) và khoảng cách từ điểm đặt lực đến trục quay \( d \). Công thức sử dụng là:

   $$ M = F \times d $$

   Ví dụ: Một lực \( F = 10 \, \text{N} \) tác dụng lên một thanh tại điểm cách trục quay \( d = 2 \, \text{m} \). Tính momen lực tác dụng lên thanh.

2. 2.2. Bài Tập Về Cân Bằng Của Vật Rắn

   Trong dạng bài tập này, bạn sẽ phải tính toán để xác định điều kiện cân bằng của một vật rắn dưới tác dụng của nhiều lực. Tổng momen lực quanh một trục phải bằng không để vật ở trạng thái cân bằng:

   $$ \sum M = 0 $$

   Ví dụ: Một thanh dài có hai lực tác dụng \( F_1 \) và \( F_2 \) ở hai đầu, với khoảng cách lần lượt là \( d_1 \) và \( d_2 \) đến trục quay. Hãy tìm điều kiện cân bằng của thanh.

3. 2.3. Bài Tập Về Ngẫu Lực

   Dạng bài tập này yêu cầu tính momen lực sinh ra bởi một cặp lực có cùng độ lớn nhưng ngược chiều, gọi là ngẫu lực. Momen ngẫu lực được tính bằng công thức:

   $$ M = F \times d $$

   Ví dụ: Một cặp lực \( F = 15 \, \text{N} \) tác dụng lên một thanh dài \( d = 0.5 \, \text{m} \). Tính momen ngẫu lực.

4. 2.4. Bài Tập Nâng Cao Về Momen Lực

   Các bài tập nâng cao thường liên quan đến lực không vuông góc với cánh tay đòn hoặc yêu cầu kết hợp nhiều nguyên lý khác nhau trong vật lý. Công thức tính momen lực trong trường hợp này là:

   $$ M = F \times d \times \sin(\theta) $$

   Ví dụ: Một lực \( F = 20 \, \text{N} \) tác dụng lên một thanh dài với góc \( \theta = 45^\circ \) so với cánh tay đòn dài \( d = 1 \, \text{m} \). Tính momen lực.

Dưới đây là một số ví dụ minh họa cụ thể về momen lực, giúp bạn hiểu rõ hơn về cách áp dụng công thức và nguyên lý của momen lực trong thực tế.

1. 3.1. Ví Dụ Tính Momen Lực Với Lực Vuông Góc

   Giả sử một lực \( F = 50 \, \text{N} \) tác dụng vuông góc lên một thanh dài tại điểm cách trục quay \( d = 2 \, \text{m} \). Tính momen lực tác dụng lên thanh.

   Bước 1: Xác định các đại lượng đã biết:

   • Lực tác dụng: \( F = 50 \, \text{N} \)
   • Khoảng cách đến trục quay: \( d = 2 \, \text{m} \)

   Bước 2: Sử dụng công thức tính momen lực:

   $$ M = F \times d = 50 \times 2 = 100 \, \text{Nm} $$

   Vậy, momen lực tác dụng lên thanh là \( 100 \, \text{Nm} \).

2. 3.2. Ví Dụ Tính Momen Lực Khi Lực Không Vuông Góc

   Giả sử một lực \( F = 30 \, \text{N} \) tác dụng lên một thanh dài tại điểm cách trục quay \( d = 1.5 \, \text{m} \), và tạo với thanh một góc \( \theta = 60^\circ \). Tính momen lực tác dụng lên thanh.

   Bước 1: Xác định các đại lượng đã biết:

   • Lực tác dụng: \( F = 30 \, \text{N} \)
   • Khoảng cách đến trục quay: \( d = 1.5 \, \text{m} \)
   • Góc giữa lực và cánh tay đòn: \( \theta = 60^\circ \)

   Bước 2: Sử dụng công thức tính momen lực khi lực không vuông góc:

   $$ M = F \times d \times \sin(\theta) = 30 \times 1.5 \times \sin(60^\circ) $$

   Bước 3: Tính giá trị của \( M \):

   $$ M = 30 \times 1.5 \times 0.866 = 38.97 \, \text{Nm} $$

   Vậy, momen lực tác dụng lên thanh là \( 38.97 \, \text{Nm} \).

3. 3.3. Ví Dụ Về Cân Bằng Của Vật Rắn

   Giả sử một thanh dài \( 4 \, \text{m} \) có hai lực tác dụng: \( F_1 = 40 \, \text{N} \) tại điểm cách đầu trái \( 1 \, \text{m} \) và \( F_2 = 60 \, \text{N} \) tại điểm cách đầu phải \( 2 \, \text{m} \). Tính khoảng cách từ điểm tựa đến đầu trái để thanh ở trạng thái cân bằng.

   Bước 1: Xác định các đại lượng đã biết:

   • Lực tác dụng: \( F_1 = 40 \, \text{N} \), \( F_2 = 60 \, \text{N} \)
   • Khoảng cách từ đầu trái: \( d_1 = 1 \, \text{m} \), \( d_2 = 2 \, \text{m} \)

   Bước 2: Sử dụng điều kiện cân bằng momen lực:

   $$ F_1 \times d_1 = F_2 \times d_2 $$

   Bước 3: Tính khoảng cách \( x \) từ điểm tựa đến đầu trái:

   $$ 40 \times x = 60 \times (4 - x) $$

   Giải phương trình trên để tìm \( x \):

   $$ 40x = 240 - 60x $$ $$ 100x = 240 $$ $$ x = 2.4 \, \text{m} $$

   Vậy, điểm tựa cần đặt cách đầu trái \( 2.4 \, \text{m} \) để thanh ở trạng thái cân bằng.

Để nắm vững kiến thức về momen lực, việc tự luyện tập với các bài tập đa dạng là rất quan trọng. Dưới đây là một số bài tập tự luyện từ cơ bản đến nâng cao, giúp bạn củng cố và phát triển khả năng giải quyết các vấn đề liên quan đến momen lực.

1. 4.1. Bài Tập Tự Luyện Cơ Bản

   • Bài 1: Một thanh dài \( 3 \, \text{m} \) được gắn cố định tại một đầu. Một lực \( F = 20 \, \text{N} \) tác dụng vuông góc tại điểm cách trục quay \( 2 \, \text{m} \). Tính momen lực tác dụng lên thanh.
   • Bài 2: Một cánh tay đòn dài \( 1.5 \, \text{m} \) chịu tác động của một lực \( F = 15 \, \text{N} \) tại điểm giữa thanh. Tính momen lực tác dụng lên cánh tay đòn.
   • Bài 3: Một lực \( F = 25 \, \text{N} \) tác dụng lên một thanh dài \( 4 \, \text{m} \) tại một góc \( \theta = 30^\circ \). Tính momen lực trong trường hợp này.

2. 4.2. Bài Tập Tự Luyện Nâng Cao

   • Bài 1: Một thanh dài \( 5 \, \text{m} \) chịu tác dụng của hai lực \( F_1 = 50 \, \text{N} \) và \( F_2 = 30 \, \text{N} \) tại hai đầu. Tính khoảng cách từ điểm tựa đến một đầu của thanh để thanh cân bằng.
   • Bài 2: Một vật rắn có ba lực tác dụng: \( F_1 = 40 \, \text{N} \), \( F_2 = 60 \, \text{N} \), và \( F_3 = 80 \, \text{N} \). Khoảng cách từ trục quay đến các điểm đặt lực lần lượt là \( 1 \, \text{m} \), \( 2 \, \text{m} \), và \( 3 \, \text{m} \). Xác định momen lực tổng hợp tác dụng lên vật rắn.
   • Bài 3: Một lực \( F = 100 \, \text{N} \) tác dụng lên một thanh dài \( 2 \, \text{m} \) tại một góc \( \theta = 45^\circ \) với thanh. Tính momen lực và xác định trạng thái cân bằng của thanh.

Dưới đây là lời giải chi tiết cho một số bài tập về momen lực, giúp bạn hiểu rõ hơn cách áp dụng công thức và phương pháp giải các bài tập từ cơ bản đến nâng cao.

1. 5.1. Giải Bài Tập Tính Momen Lực Đơn Giản

   Bài toán: Một lực \( F = 20 \, \text{N} \) tác dụng vuông góc lên một thanh dài tại điểm cách trục quay \( d = 1.5 \, \text{m} \). Tính momen lực tác dụng lên thanh.

   Lời giải:

   1. Xác định các đại lượng đã biết:
      • Lực tác dụng: \( F = 20 \, \text{N} \)
      • Khoảng cách đến trục quay: \( d = 1.5 \, \text{m} \)
   2. Sử dụng công thức tính momen lực:

      $$ M = F \times d $$

      Thay các giá trị đã biết vào công thức:

      $$ M = 20 \times 1.5 = 30 \, \text{Nm} $$

   3. Kết luận: Momen lực tác dụng lên thanh là \( 30 \, \text{Nm} \).

2. 5.2. Giải Bài Tập Về Cân Bằng Của Vật Rắn

   Bài toán: Một thanh dài \( 4 \, \text{m} \) chịu tác động của hai lực \( F_1 = 40 \, \text{N} \) tại điểm cách đầu trái \( 1 \, \text{m} \) và \( F_2 = 60 \, \text{N} \) tại điểm cách đầu phải \( 2 \, \text{m} \). Tìm vị trí đặt điểm tựa để thanh cân bằng.

   Lời giải:

   1. Xác định các đại lượng đã biết:
      • Lực tác dụng: \( F_1 = 40 \, \text{N} \), \( F_2 = 60 \, \text{N} \)
      • Khoảng cách từ điểm tựa đến các lực: \( x_1 = 1 \, \text{m} \), \( x_2 = 2 \, \text{m} \)
   2. Sử dụng điều kiện cân bằng momen lực:

      $$ F_1 \times x_1 = F_2 \times x_2 $$

      Giải phương trình để tìm vị trí đặt điểm tựa:

      $$ 40 \times x = 60 \times (4 - x) $$

      Giải phương trình:

      $$ 40x = 240 - 60x $$ $$ 100x = 240 $$ $$ x = 2.4 \, \text{m} $$

   3. Kết luận: Điểm tựa cần đặt cách đầu trái \( 2.4 \, \text{m} \) để thanh ở trạng thái cân bằng.

3. 5.3. Giải Bài Tập Về Ngẫu Lực

   Bài toán: Hai lực có độ lớn \( F_1 = 50 \, \text{N} \) và \( F_2 = 50 \, \text{N} \) tác dụng ngược chiều lên hai đầu của một thanh dài \( 3 \, \text{m} \). Tính momen ngẫu lực.

   Lời giải:

   1. Xác định các đại lượng đã biết:
      • Lực tác dụng: \( F_1 = F_2 = 50 \, \text{N} \)
      • Khoảng cách giữa hai điểm tác dụng lực: \( d = 3 \, \text{m} \)
   2. Sử dụng công thức tính momen ngẫu lực:

      $$ M = F \times d $$

      Thay các giá trị đã biết vào công thức:

      $$ M = 50 \times 3 = 150 \, \text{Nm} $$

   3. Kết luận: Momen ngẫu lực tác dụng lên thanh là \( 150 \, \text{Nm} \).

Việc nghiên cứu và nắm vững quy tắc momen lực là vô cùng quan trọng trong lĩnh vực vật lý. Dưới đây là một số tài liệu tham khảo hữu ích giúp bạn hiểu rõ hơn về chủ đề này, từ các sách giáo khoa đến tài liệu trực tuyến và các bài giảng nâng cao.

• Sách Giáo Khoa Vật Lý:
  • Vật Lý 10 - Bộ Giáo Dục và Đào Tạo: Cuốn sách cung cấp những kiến thức nền tảng về momen lực và các nguyên lý liên quan, phù hợp cho học sinh trung học phổ thông.
  • Vật Lý Cơ Bản - Nguyễn Đình Dương: Sách cung cấp các ví dụ minh họa và bài tập phong phú về momen lực, giúp học sinh và sinh viên hiểu sâu hơn về chủ đề.
• Các Bài Giảng Trực Tuyến:
  • Khan Academy: Trang web cung cấp các video bài giảng và bài tập trực tuyến về quy tắc momen lực, từ cơ bản đến nâng cao.
  • Học247: Nền tảng này cung cấp các bài giảng trực tuyến bằng tiếng Việt với nhiều ví dụ thực tiễn về momen lực.
• Tài Liệu Nâng Cao Về Momen Lực:
  • Cơ Học Lý Thuyết - Trần Ngọc Hợi: Cuốn sách dành cho sinh viên đại học chuyên ngành vật lý và kỹ thuật, cung cấp các phân tích chi tiết và bài tập nâng cao về momen lực.
  • Physics for Scientists and Engineers - Serway & Jewett: Sách giáo trình quốc tế dành cho sinh viên, bao gồm cả phần lý thuyết và bài tập về momen lực ở mức độ cao cấp.