Chủ đề lực đẩy acsimet có phương và chiều như thế nào: Lực đẩy Ác-si-mét có phương và chiều như thế nào? Bài viết này sẽ giải đáp chi tiết về lực đẩy Ác-si-mét, cách xác định phương và chiều, cùng các ví dụ thực tế về ứng dụng trong đời sống và khoa học. Khám phá ngay để hiểu rõ hơn về nguyên lý nổi của vật thể và những ứng dụng quan trọng của nó!
Mục lục
Lực Đẩy Archimedes: Phương và Chiều
Lực đẩy Archimedes là một trong những nguyên lý quan trọng trong vật lý học chất lỏng. Nó giải thích tại sao vật thể có thể nổi hoặc chìm khi đặt trong một chất lỏng. Dưới đây là các thông tin chi tiết về lực đẩy này, phương và chiều của nó.
1. Phát Biểu Nguyên Lý Archimedes
Nguyên lý Archimedes phát biểu rằng: "Bất kỳ vật thể nào nhúng trong chất lỏng sẽ chịu một lực đẩy từ dưới lên bằng trọng lượng của lượng chất lỏng bị vật thể chiếm chỗ."
2. Phương của Lực Đẩy Archimedes
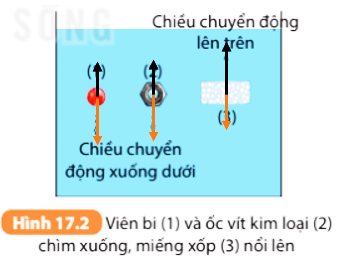
Phương của lực đẩy Archimedes luôn thẳng đứng. Điều này là do sự chênh lệch áp suất tại các điểm khác nhau trên bề mặt của vật thể nhúng trong chất lỏng. Áp suất dưới đáy vật thể lớn hơn áp suất ở phần trên, do đó tạo ra một lực đẩy hướng từ dưới lên.
3. Chiều của Lực Đẩy Archimedes
Chiều của lực đẩy Archimedes luôn hướng từ dưới lên trên. Lực này giúp các vật thể như thuyền, tàu ngầm, hoặc khinh khí cầu nổi lên trong chất lỏng hoặc không khí. Nếu lực đẩy lớn hơn trọng lượng của vật, vật sẽ nổi; nếu bằng trọng lượng, vật sẽ lơ lửng; và nếu nhỏ hơn, vật sẽ chìm.
4. Công Thức Tính Lực Đẩy Archimedes
Lực đẩy Archimedes có thể được tính toán bằng công thức:
\( F_A = \rho \cdot V \cdot g \)
Trong đó:
- \( F_A \) là lực đẩy Archimedes (N).
- \( \rho \) là khối lượng riêng của chất lỏng (kg/m³).
- \( V \) là thể tích của phần vật thể bị chiếm chỗ trong chất lỏng (m³).
- \( g \) là gia tốc trọng trường (m/s²), thông thường giá trị là 9,8 m/s².
5. Ứng Dụng Thực Tiễn của Lực Đẩy Archimedes
Lực đẩy Archimedes có nhiều ứng dụng thực tiễn trong cuộc sống:
- Thiết kế và đóng tàu thuyền: Tàu thuyền nổi trên mặt nước nhờ lực đẩy Archimedes cân bằng với trọng lượng của chúng.
- Khinh khí cầu và khí cầu: Chúng bay lên nhờ lực đẩy Archimedes trong không khí khi khí cầu được bơm đầy khí nhẹ hơn không khí.
- Đo lường khối lượng và thể tích: Lực đẩy Archimedes được ứng dụng trong các thiết bị đo lường để xác định khối lượng và thể tích của vật thể.
- Nguyên lý hoạt động của tàu ngầm: Tàu ngầm điều chỉnh lượng nước trong khoang để thay đổi lực đẩy Archimedes, từ đó lặn xuống hoặc nổi lên.
6. Kết Luận
Lực đẩy Archimedes là một khái niệm cơ bản và quan trọng trong vật lý học, giúp chúng ta hiểu rõ hơn về cách các vật thể tương tác với chất lỏng và khí. Từ đó, nó có nhiều ứng dụng thiết thực trong các ngành công nghiệp và đời sống hàng ngày.

.png)
I. Khái niệm và công thức lực đẩy Ác-si-mét
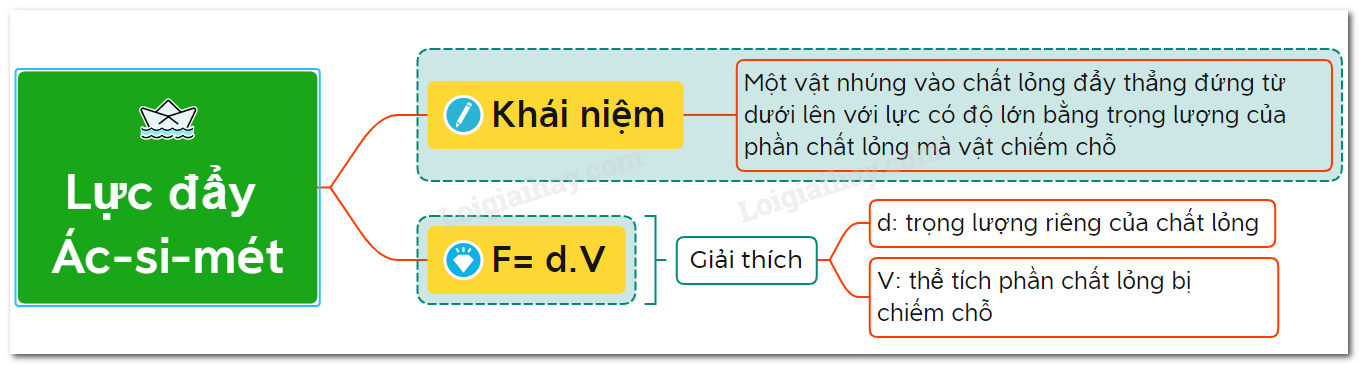
Lực đẩy Ác-si-mét là lực xuất hiện khi một vật thể được nhúng vào chất lỏng hoặc chất khí. Lực này được đặt tên theo nhà khoa học Hy Lạp cổ đại, Archimedes, người đã phát hiện ra nguyên lý quan trọng này. Nguyên lý Ác-si-mét phát biểu rằng: “Một vật thể chìm trong chất lỏng chịu một lực đẩy từ dưới lên có độ lớn bằng trọng lượng của phần chất lỏng mà nó chiếm chỗ”. Lực đẩy này giúp giải thích tại sao một số vật thể có thể nổi hoặc chìm khi được thả vào chất lỏng.
- Phương: Lực đẩy Ác-si-mét có phương thẳng đứng.
- Chiều: Lực đẩy này có chiều từ dưới lên, ngược chiều với trọng lực của vật.
Công thức tính lực đẩy Ác-si-mét:
Công thức tính lực đẩy Ác-si-mét được biểu diễn như sau:
Trong đó:
- \(\rho\): Khối lượng riêng của chất lỏng (kg/m³).
- V: Thể tích phần vật thể chìm trong chất lỏng (m³).
- g: Gia tốc trọng trường, thường lấy giá trị xấp xỉ 9,81 m/s².
Ví dụ: Nếu một vật thể có thể tích 2 m³ chìm hoàn toàn trong nước (với khối lượng riêng của nước là 1000 kg/m³), thì lực đẩy Ác-si-mét tác dụng lên vật thể đó được tính như sau:
| Khối lượng riêng của nước (\(\rho\)) | 1000 kg/m³ |
| Thể tích vật thể chìm (V) | 2 m³ |
| Gia tốc trọng trường (g) | 9,81 m/s² |
| Lực đẩy Ác-si-mét (FA) | 1000 x 2 x 9,81 = 19.620 N |
Như vậy, lực đẩy Ác-si-mét tác động lên vật thể trong ví dụ trên là 19.620 N.
II. Các yếu tố ảnh hưởng đến lực đẩy Ác-si-mét
Lực đẩy Ác-si-mét bị ảnh hưởng bởi nhiều yếu tố khác nhau. Những yếu tố này đóng vai trò quan trọng trong việc xác định liệu một vật thể sẽ nổi, chìm hay lơ lửng khi được đặt trong chất lỏng. Dưới đây là các yếu tố chính:
- Thể tích phần chìm của vật thể (V):
Thể tích phần chìm của vật thể trong chất lỏng quyết định lượng chất lỏng mà vật thể chiếm chỗ. Thể tích phần chìm càng lớn thì lực đẩy Ác-si-mét càng mạnh. Công thức lực đẩy Ác-si-mét bao gồm biến số thể tích (V), do đó khi thể tích tăng, lực đẩy cũng tăng theo.
- Khối lượng riêng của chất lỏng (\(\rho\)):
Khối lượng riêng của chất lỏng cũng ảnh hưởng trực tiếp đến lực đẩy Ác-si-mét. Nếu chất lỏng có khối lượng riêng lớn hơn, lực đẩy tác dụng lên vật thể sẽ lớn hơn. Ví dụ, nước biển có khối lượng riêng cao hơn nước ngọt, do đó vật thể sẽ nổi dễ dàng hơn trong nước biển.
- Gia tốc trọng trường (g):
Gia tốc trọng trường là hằng số ảnh hưởng đến lực đẩy. Trên Trái Đất, giá trị này thường được lấy là 9,81 m/s². Tuy nhiên, trong những môi trường có gia tốc trọng trường khác (như trên Mặt Trăng), lực đẩy Ác-si-mét sẽ thay đổi.
- Hình dạng và vị trí của vật thể:
Hình dạng của vật thể ảnh hưởng đến cách áp suất phân bố trên bề mặt của nó, từ đó tác động đến lực đẩy Ác-si-mét. Vị trí của vật thể trong chất lỏng cũng ảnh hưởng đến áp suất tại các điểm khác nhau, gây ra lực đẩy không đồng đều.
Để tính toán cụ thể lực đẩy Ác-si-mét, chúng ta có thể sử dụng công thức sau:
Trong đó:
- \(\rho\): Khối lượng riêng của chất lỏng (kg/m³).
- V: Thể tích phần vật thể chìm trong chất lỏng (m³).
- g: Gia tốc trọng trường (m/s²).
Ví dụ: Nếu một vật có thể tích 3 m³ chìm trong nước biển với khối lượng riêng là 1025 kg/m³, thì lực đẩy Ác-si-mét sẽ được tính như sau:
| Khối lượng riêng của nước biển (\(\rho\)) | 1025 kg/m³ |
| Thể tích vật thể chìm (V) | 3 m³ |
| Gia tốc trọng trường (g) | 9,81 m/s² |
| Lực đẩy Ác-si-mét (FA) | 1025 x 3 x 9,81 = 30.172,5 N |
Như vậy, lực đẩy Ác-si-mét tác động lên vật thể này là 30.172,5 N.

III. Ứng dụng của lực đẩy Ác-si-mét trong thực tế
Lực đẩy Ác-si-mét có nhiều ứng dụng quan trọng trong đời sống và khoa học. Hiểu rõ nguyên lý này giúp chúng ta thiết kế các thiết bị và công trình nổi trong nước, hỗ trợ nhiều ngành công nghiệp và đời sống hàng ngày. Dưới đây là một số ứng dụng phổ biến của lực đẩy Ác-si-mét:
- Thiết kế tàu, thuyền và các phương tiện nổi:
Nguyên lý Ác-si-mét được ứng dụng rộng rãi trong thiết kế tàu, thuyền và phà. Các kỹ sư sử dụng nguyên lý này để tính toán kích thước và hình dạng của tàu sao cho lực đẩy đủ để tàu nổi trên mặt nước, ngay cả khi chở nhiều hàng hóa hoặc hành khách.
- Khinh khí cầu và các phương tiện bay:
Khinh khí cầu sử dụng lực đẩy Ác-si-mét trong khí quyển. Thể tích khí nóng hoặc khí nhẹ hơn không khí (như helium) bên trong khinh khí cầu tạo ra lực đẩy ngược lại với trọng lực, giúp khinh khí cầu có thể bay lên cao.
- Sự nổi của cá và các sinh vật biển:
Các loài cá và động vật biển sử dụng bong bóng khí bên trong cơ thể để điều chỉnh độ nổi của chúng trong nước, một cơ chế hoạt động dựa trên lực đẩy Ác-si-mét. Điều này cho phép chúng có thể di chuyển lên và xuống trong môi trường nước một cách dễ dàng.
- Đo mật độ vật liệu:
Lực đẩy Ác-si-mét cũng được ứng dụng trong việc xác định mật độ của các vật liệu. Bằng cách đo lực đẩy của một vật thể khi nó chìm trong chất lỏng, người ta có thể tính toán mật độ của vật liệu đó theo công thức:
$$ \rho = \frac{\text{Trọng lượng vật thể trong không khí}}{\text{Lực đẩy Ác-si-mét}} $$
Những ứng dụng này không chỉ thể hiện tầm quan trọng của lực đẩy Ác-si-mét trong lý thuyết mà còn trong nhiều lĩnh vực thực tiễn, giúp cải tiến công nghệ và phát triển xã hội.

XEM THÊM:
IV. Bài tập vận dụng liên quan đến lực đẩy Ác-si-mét
Bài tập về lực đẩy Ác-si-mét thường xoay quanh việc tính toán lực đẩy, xác định điều kiện nổi/chìm của vật thể, và ứng dụng nguyên lý này vào các tình huống thực tế. Dưới đây là một số bài tập giúp học sinh, sinh viên hiểu rõ hơn về lực đẩy Ác-si-mét:
- Bài tập tính lực đẩy Ác-si-mét:
Một vật thể hình hộp có thể tích 0,5 m³ được thả vào nước có khối lượng riêng là 1000 kg/m³. Tính lực đẩy Ác-si-mét tác dụng lên vật thể.
Lời giải: Áp dụng công thức tính lực đẩy Ác-si-mét:
$$ F_A = \rho \cdot V \cdot g $$ Thay số:
- \(\rho = 1000 \, \text{kg/m}^3\)
- V = 0,5 m³
- g = 9,81 m/s²
Ta có:
$$ F_A = 1000 \cdot 0,5 \cdot 9,81 = 4905 \, \text{N} $$ Vậy, lực đẩy Ác-si-mét tác dụng lên vật thể là 4905 N.
- Bài tập về điều kiện nổi/chìm:
Một vật có khối lượng 800 kg và thể tích 1 m³ được thả vào nước. Hãy xác định liệu vật có nổi hay chìm.
Lời giải: Điều kiện nổi/chìm phụ thuộc vào so sánh giữa lực đẩy Ác-si-mét và trọng lực của vật.
- Trọng lượng của vật: \( P = m \cdot g = 800 \cdot 9,81 = 7848 \, \text{N} \)
- Lực đẩy Ác-si-mét: \( F_A = \rho \cdot V \cdot g = 1000 \cdot 1 \cdot 9,81 = 9810 \, \text{N} \)
Vì \( F_A > P \), nên vật sẽ nổi lên mặt nước.
- Bài tập thực hành trong phòng thí nghiệm:
Sử dụng cân lực kế để đo lực đẩy Ác-si-mét khi một vật thể chìm trong chất lỏng. Thực hiện các phép đo với nhiều chất lỏng có khối lượng riêng khác nhau như nước, dầu và rượu, để xác định mối quan hệ giữa khối lượng riêng của chất lỏng và lực đẩy.
Những bài tập trên giúp người học nắm vững hơn nguyên lý Ác-si-mét và cách ứng dụng nó vào việc giải quyết các bài toán thực tế.