Vật Lý 8 Bài 17: Khám Phá Lực Đẩy Ác-si-mét Và Ứng Dụng Trong Thực Tiễn

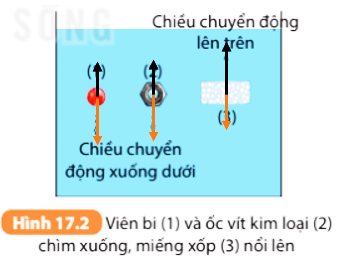
Trong bài học về lực đẩy Ác-si-mét, học sinh được tìm hiểu về hiện tượng một vật khi nhúng vào chất lỏng sẽ chịu tác động của một lực đẩy từ phía dưới lên trên. Đây là lực đẩy Ác-si-mét, đặt tên theo nhà khoa học Archimedes, và là một kiến thức quan trọng trong chương trình Vật lý lớp 8.

1. Công Thức Tính Lực Đẩy Ác-Si-Mét

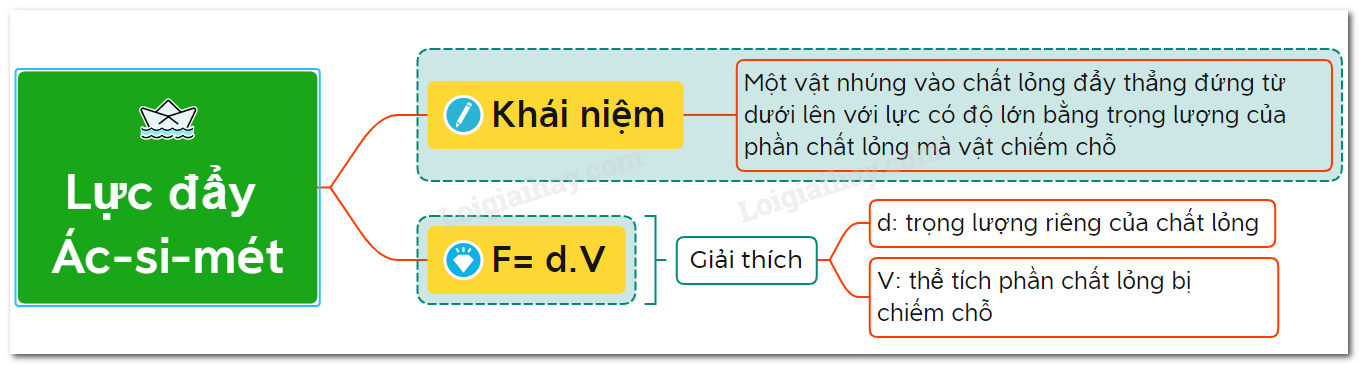
Lực đẩy Ác-si-mét được xác định bằng công thức:

\( F_A = d \cdot V \)

• \( d \): Trọng lượng riêng của chất lỏng (N/m³)
• \( V \): Thể tích phần chất lỏng bị vật chiếm chỗ (m³)

2. Các Trường Hợp Tính Thể Tích Phần Chìm

• Nếu vật chìm hoàn toàn: \( V_{chìm} = V_{vật} \)
• Nếu vật có một phần nổi: \( V_{chìm} = V_{vật} - V_{nổi} \)
• Nếu cho biết chiều cao phần chìm: \( V_{chìm} = S_{đáy} \times h \)

3. Các Đặc Điểm Của Lực Đẩy Ác-Si-Mét

• Khi các vật được nhúng chìm trong cùng một chất lỏng, lực đẩy Ác-si-mét chỉ phụ thuộc vào thể tích vật.
• Khi các vật có cùng khối lượng nhưng làm từ chất khác nhau, lực đẩy phụ thuộc vào khối lượng riêng của chất liệu.
• Nếu các vật có cùng thể tích nhưng được nhúng vào các chất lỏng khác nhau, lực đẩy sẽ lớn hơn đối với chất lỏng có trọng lượng riêng lớn hơn.

4. Ví Dụ Bài Tập Trắc Nghiệm

Dưới đây là một số câu hỏi trắc nghiệm liên quan đến lực đẩy Ác-si-mét:

1. Một vật chìm hoàn toàn trong nước sẽ chịu tác động của những lực nào?
   Đáp án: Trọng lực và lực đẩy Ác-si-mét.
2. Lực đẩy Ác-si-mét bằng trọng lượng của phần chất lỏng nào?
   Đáp án: Trọng lượng phần chất lỏng bị vật chiếm chỗ.

5. Kết Luận

Hiểu về lực đẩy Ác-si-mét giúp học sinh không chỉ nắm vững kiến thức lý thuyết mà còn ứng dụng được vào các bài tập thực tiễn, như tính toán khối lượng, thể tích và lực tác động lên các vật trong chất lỏng.

Lực đẩy Ác-si-mét là một trong những nguyên lý cơ bản trong vật lý, được nhà khoa học Archimedes phát hiện từ thời cổ đại. Nguyên lý này giải thích hiện tượng khi một vật thể bị chìm vào trong chất lỏng, nó sẽ chịu tác động của một lực đẩy ngược lên từ phía chất lỏng. Lực này được gọi là lực đẩy Ác-si-mét và có cường độ bằng với trọng lượng của phần chất lỏng mà vật thể chiếm chỗ. Công thức tính lực đẩy Ác-si-mét là:

\[ F_A = d \times V \]

• d là trọng lượng riêng của chất lỏng (N/m³).
• V là thể tích phần chất lỏng bị vật chiếm chỗ (m³).

Ứng dụng của lực đẩy Ác-si-mét rất rộng rãi trong đời sống, từ việc thiết kế tàu thuyền, tàu ngầm cho đến việc giải thích các hiện tượng tự nhiên như sự nổi của vật trong nước. Khám phá này đã đóng góp quan trọng vào sự phát triển của khoa học và công nghệ, đặc biệt là trong lĩnh vực cơ học chất lỏng.

Lực đẩy Ác-si-mét là lực đẩy do chất lỏng tác dụng lên một vật khi nó được nhúng trong chất lỏng. Để xác định độ lớn của lực đẩy này, ta sử dụng công thức sau:

$$ F_A = d \cdot V $$

Trong đó:

• F_A: Lực đẩy Ác-si-mét (N)
• d: Trọng lượng riêng của chất lỏng (N/m³)
• V: Thể tích phần chất lỏng bị vật chiếm chỗ (m³)

Để tính toán lực đẩy Ác-si-mét, bạn cần xác định hai yếu tố chính:

1. Trọng lượng riêng của chất lỏng: Thường được ký hiệu là d, đây là một giá trị cố định cho mỗi loại chất lỏng. Ví dụ, đối với nước, trọng lượng riêng là 10,000 N/m³.
2. Thể tích của vật: Khi vật hoàn toàn chìm trong chất lỏng, thể tích này là thể tích của toàn bộ vật. Trong trường hợp vật chỉ chìm một phần, thể tích này chỉ là phần thể tích bị chìm trong chất lỏng.

Với công thức trên, bạn có thể tính toán lực đẩy Ác-si-mét cho bất kỳ vật nào khi biết được trọng lượng riêng của chất lỏng và thể tích của vật đó.

Ví dụ: Một vật có khối lượng 0,5 kg và khối lượng riêng là 2,500 kg/m³ được nhúng hoàn toàn trong nước. Hãy tính lực đẩy Ác-si-mét tác dụng lên vật.

Giải: Trước tiên, chúng ta cần tính thể tích của vật:

$$ V = \frac{m}{D} = \frac{0,5 \text{ kg}}{2,500 \text{ kg/m}^3} = 0,0002 \text{ m}^3 $$

Sau đó, áp dụng công thức lực đẩy Ác-si-mét:

$$ F_A = d \cdot V = 10,000 \text{ N/m}^3 \cdot 0,0002 \text{ m}^3 = 2 \text{ N} $$

Vậy lực đẩy Ác-si-mét tác dụng lên vật là 2 N.

Để hiểu rõ hơn về lực đẩy Ác-si-mét, dưới đây là một số bài tập và ví dụ minh họa giúp bạn áp dụng các kiến thức đã học vào thực tiễn:

• Bài tập 1: Một vật có khối lượng 2 kg được nhúng chìm hoàn toàn trong nước. Biết trọng lượng riêng của nước là \(10,000 \, \text{N/m}^3\). Hãy tính lực đẩy Ác-si-mét tác dụng lên vật.

Lời giải:

Trọng lượng của vật trong không khí: \(P = m \cdot g = 2 \cdot 10 = 20 \, \text{N}\)

Lực đẩy Ác-si-mét: \(F_A = d \cdot V = 10,000 \cdot V\)

Vì vật chìm hoàn toàn trong nước nên lực đẩy Ác-si-mét và trọng lực của vật bằng nhau, do đó: \(F_A = P = 20 \, \text{N}\). Từ đó tính được thể tích vật: \(V = \frac{F_A}{d} = \frac{20}{10,000} = 0.002 \, \text{m}^3\).

• Bài tập 2: Một quả cầu có thể tích 600 cm³ và khối lượng 0.5 kg được thả vào nước. Hãy cho biết liệu quả cầu có chìm hoàn toàn hay không.

Lời giải:

Trọng lượng của quả cầu: \(P = 0.5 \cdot 10 = 5 \, \text{N}\).

Lực đẩy Ác-si-mét nếu quả cầu chìm hoàn toàn: \(F_A = d \cdot V = 10,000 \cdot 0.0006 = 6 \, \text{N}\).

Vì \(F_A > P\), quả cầu sẽ nổi trên mặt nước, không chìm hoàn toàn.

• Bài tập 3: Một khối nước đá hình lập phương có cạnh 5 cm và khối lượng riêng 0.9 g/cm³. Tính tỷ số giữa thể tích phần nổi và phần chìm của khối nước đá khi nó nổi trên mặt nước.

Lời giải:

Thể tích của khối nước đá: \(V = 5 \cdot 5 \cdot 5 = 125 \, \text{cm}^3\).

Khối lượng nước đá: \(m = 0.9 \cdot 125 = 112.5 \, \text{g}\).

Lực đẩy Ác-si-mét: \(F_A = d \cdot V = 10000 \cdot V_{chìm}\).

Tỷ số giữa thể tích phần nổi và phần chìm được xác định dựa trên cân bằng giữa trọng lực và lực đẩy.

Thí nghiệm về lực đẩy Ác-si-mét là một trong những cách đơn giản và hiệu quả nhất để minh họa và kiểm chứng định luật này. Dưới đây là hướng dẫn chi tiết cách thực hiện thí nghiệm:

1. Chuẩn bị dụng cụ:
   • Một lực kế có giới hạn đo từ 0 đến 2N.
   • Một quả cân nhỏ bằng nhựa có khối lượng khoảng 130g.
   • Một bình tràn và một ống đong để đo thể tích nước tràn ra.
   • Một giá treo thí nghiệm.
2. Tiến hành thí nghiệm:
   1. Đo trọng lượng vật: Treo quả cân vào lực kế và ghi lại giá trị trọng lượng P₀.
   2. Nhúng vật vào nước: Từ từ nhúng quả cân vào bình tràn chứa nước sao cho không để vật chạm đáy hay thành bình. Nước sẽ bị đẩy ra và chảy vào ống đong.
   3. Đo lực đẩy: Ghi lại giá trị mới trên lực kế là P. Sự khác biệt giữa P₀ và P chính là lực đẩy Ác-si-mét F_A.
   4. Tính toán: Thể tích nước tràn ra V chính là thể tích của phần vật chìm trong nước. Áp dụng công thức:

Công thức tính lực đẩy Ác-si-mét:

F_{A} = d \cdot V

Trong đó:

• d là trọng lượng riêng của chất lỏng (N/m³).
• V là thể tích phần chất lỏng bị vật chiếm chỗ (m³).

Kết quả thí nghiệm này sẽ cho thấy lực đẩy Ác-si-mét phụ thuộc trực tiếp vào thể tích của phần vật chìm trong nước và trọng lượng riêng của chất lỏng. Đây là minh chứng rõ ràng và trực quan cho định luật Ác-si-mét.

Lực đẩy Ác-si-mét không chỉ là một hiện tượng vật lý thú vị mà còn có nhiều ứng dụng thực tiễn trong đời sống hàng ngày. Dưới đây là một số ví dụ điển hình về cách lực đẩy Ác-si-mét được vận dụng:

1. Tàu thuyền: Nhờ vào lực đẩy Ác-si-mét, tàu thuyền có thể nổi trên mặt nước dù chúng có trọng lượng lớn. Để tàu có thể nổi, thể tích của nước bị tàu chiếm chỗ phải tạo ra lực đẩy đủ lớn để cân bằng với trọng lượng của tàu.
2. Khinh khí cầu: Khinh khí cầu bay lên nhờ vào lực đẩy Ác-si-mét trong không khí. Khinh khí cầu chứa đầy khí nhẹ hơn không khí xung quanh (như heli hoặc hydro), tạo ra lực đẩy đủ lớn để nâng khinh khí cầu lên không trung.
3. Thiết kế tàu ngầm: Tàu ngầm vận dụng nguyên lý lực đẩy Ác-si-mét để điều chỉnh độ nổi của mình. Khi tàu ngầm cần nổi lên, nó giảm trọng lượng bằng cách đẩy nước ra ngoài. Ngược lại, khi cần lặn xuống, tàu ngầm tăng trọng lượng bằng cách hút nước vào các bể chứa, làm giảm lực đẩy Ác-si-mét.
4. Đo khối lượng riêng của chất rắn: Lực đẩy Ác-si-mét cũng được sử dụng để đo khối lượng riêng của một vật. Bằng cách so sánh trọng lượng của vật trong không khí và trong nước, có thể tính toán được lực đẩy Ác-si-mét và từ đó suy ra khối lượng riêng của vật.

Như vậy, lực đẩy Ác-si-mét không chỉ là một khái niệm lý thuyết mà còn là một lực có ý nghĩa lớn trong khoa học và công nghệ, góp phần giải thích và ứng dụng nhiều hiện tượng tự nhiên cũng như kỹ thuật hiện đại.

Trong phần này, chúng ta sẽ củng cố kiến thức về lực đẩy Ác-si-mét qua một số câu hỏi và bài tập chọn lọc. Các câu hỏi sẽ giúp học sinh ôn tập lại lý thuyết và áp dụng vào thực tiễn, từ đó nắm vững hơn về khái niệm và công thức liên quan.

• Bài tập 1: Một vật có thể tích 0,5 m³ được nhúng chìm hoàn toàn trong nước. Hãy tính lực đẩy Ác-si-mét tác dụng lên vật đó. Biết rằng trọng lượng riêng của nước là 10000 N/m³.

Giải: Sử dụng công thức: \( F_A = d \cdot V \)

Trong đó:

• d = 10000 N/m³ (trọng lượng riêng của nước)
• V = 0,5 m³ (thể tích của vật)

Vậy lực đẩy Ác-si-mét tác dụng lên vật là:

\[ F_A = 10000 \times 0,5 = 5000 \, \text{N} \]

Đáp án: 5000 N

• Bài tập 2: Một khối kim loại có thể tích 0,3 m³, khối lượng riêng là 7800 kg/m³, được thả vào nước. Hãy xác định lực đẩy Ác-si-mét tác dụng lên khối kim loại đó và liệu nó sẽ chìm hay nổi.

Giải: Sử dụng công thức: \( F_A = d \cdot V \)

Với:

• d = 10000 N/m³ (trọng lượng riêng của nước)
• V = 0,3 m³ (thể tích của khối kim loại)

Lực đẩy Ác-si-mét tác dụng lên khối kim loại là:

\[ F_A = 10000 \times 0,3 = 3000 \, \text{N} \]

So sánh với trọng lượng của khối kim loại:

\[ P = m \times g = \rho \times V \times g = 7800 \times 0,3 \times 9,8 = 22842 \, \text{N} \]

Vì trọng lượng của khối kim loại lớn hơn lực đẩy Ác-si-mét nên khối kim loại sẽ chìm.

• Bài tập 3: Một quả cầu có thể tích 0,2 m³ được treo trong không khí và nhúng chìm trong dầu có trọng lượng riêng là 8000 N/m³. Tính lực đẩy Ác-si-mét tác dụng lên quả cầu khi nhúng chìm hoàn toàn trong dầu.

Giải: Sử dụng công thức: \( F_A = d \cdot V \)

Với:

• d = 8000 N/m³ (trọng lượng riêng của dầu)
• V = 0,2 m³ (thể tích của quả cầu)

Lực đẩy Ác-si-mét tác dụng lên quả cầu là:

\[ F_A = 8000 \times 0,2 = 1600 \, \text{N} \]

Đáp án: 1600 N

Qua các bài tập trên, học sinh có thể thấy rõ hơn cách tính lực đẩy Ác-si-mét và hiểu sâu hơn về nguyên lý hoạt động của nó trong các tình huống thực tế.

Lực đẩy Ác-si-mét là một lực có vai trò quan trọng trong nhiều lĩnh vực của đời sống và kỹ thuật. Lực này giúp chúng ta hiểu rõ hơn về hiện tượng nổi của các vật thể trong chất lỏng, từ đó áp dụng vào các ngành như hàng hải, thủy lợi, và cả trong y học.

• Nguyên lý cơ bản: Lực đẩy Ác-si-mét tác dụng lên bất kỳ vật thể nào bị nhúng vào chất lỏng, có phương thẳng đứng từ dưới lên và có độ lớn bằng trọng lượng của chất lỏng bị vật chiếm chỗ. Điều này giải thích vì sao một số vật nổi trên nước trong khi các vật khác lại chìm.
• Ứng dụng trong đời sống: Nguyên lý này được ứng dụng rộng rãi trong thiết kế tàu thuyền, làm nổi bật sự cân bằng giữa trọng lượng của tàu và lực đẩy do nước tác dụng lên tàu. Ngoài ra, lực đẩy Ác-si-mét cũng được áp dụng trong việc xác định khối lượng riêng của các vật liệu và trong y học để đo thể tích của các phần cơ thể.
• Ứng dụng trong kỹ thuật: Các kỹ sư sử dụng nguyên lý Ác-si-mét để thiết kế các công trình thủy điện, các hệ thống lọc nước, và các phương tiện nổi như phao cứu sinh. Khả năng của vật thể nổi hay chìm cũng giúp tạo nên các sản phẩm như tàu ngầm và phao khí tượng.

Hiểu biết về lực đẩy Ác-si-mét không chỉ giúp chúng ta lý giải các hiện tượng tự nhiên mà còn góp phần vào việc phát triển nhiều ngành công nghiệp quan trọng. Điều này khẳng định tầm quan trọng và giá trị thực tiễn của lực đẩy Ác-si-mét trong khoa học và kỹ thuật.