Các Dạng Bài Tập Về Lực Đẩy Acsimet: Hướng Dẫn Chi Tiết và Lời Giải Đầy Đủ

Lực đẩy Ác-si-mét là một khái niệm quan trọng trong vật lý, đặc biệt là khi nghiên cứu về chất lỏng. Dưới đây là một số dạng bài tập thường gặp và phương pháp giải quyết.

1. Công Thức Tính Lực Đẩy Ác-Si-Mét

Lực đẩy Ác-si-mét được xác định bởi công thức:

\[ F_A = d \cdot V \]

Trong đó:

• F_A: Lực đẩy Ác-si-mét (N)
• d: Trọng lượng riêng của chất lỏng (N/m³)
• V: Thể tích phần chất lỏng bị vật chiếm chỗ (m³)

2. Tính Chất Của Lực Đẩy Ác-Si-Mét

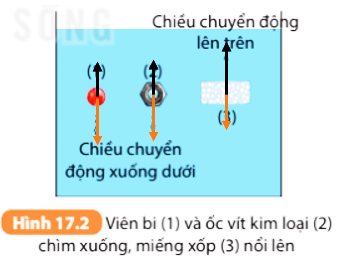
• Lực đẩy Ác-si-mét có phương thẳng đứng, từ dưới lên trên.
• Điểm đặt của lực đẩy tại trọng tâm của phần chất lỏng bị chiếm chỗ.
• Độ lớn của lực đẩy bằng trọng lượng của phần chất lỏng mà vật chiếm chỗ.

3. Các Dạng Bài Tập Thường Gặp

Dạng 1: Tính Lực Đẩy Ác-Si-Mét

Cho một vật có thể tích V, nhúng chìm hoàn toàn vào chất lỏng có trọng lượng riêng d. Tính lực đẩy Ác-si-mét tác dụng lên vật.

Lời giải:

Sử dụng công thức lực đẩy Ác-si-mét:

\[ F_A = d \cdot V \]

Thay số vào để tính toán kết quả.

Dạng 2: So Sánh Lực Đẩy Trên Các Vật Có Khối Lượng Bằng Nhau

Hai vật có khối lượng bằng nhau, được làm từ hai chất liệu khác nhau (nhôm và hợp kim) và nhúng chìm trong cùng một chất lỏng. Hãy xác định lực đẩy Ác-si-mét tác dụng lên mỗi vật và so sánh.

Lời giải:

Với cùng khối lượng, thể tích của hai vật sẽ khác nhau. Ta có:

\[ F_{A1} = d_n \cdot \frac{m}{d_1}, \quad F_{A2} = d_n \cdot \frac{m}{d_2} \]

So sánh hai lực đẩy để tìm ra vật nào chịu tác dụng lực lớn hơn.

Dạng 3: Bài Tập Về Sự Nổi

Đặt một khối gỗ hình hộp có tiết diện S và chiều cao h thẳng đứng trong nước. Tính công cần thiết để nhấn chìm khối gỗ xuống đáy hồ.

Lời giải:

Xác định thể tích khối gỗ và trọng lượng của nó, sau đó tính lực đẩy Ác-si-mét. Công thực hiện được tính bằng công thức:

\[ A = F \cdot d \]

Với F là lực cần thiết và d là quãng đường.

Dạng 4: Ứng Dụng Lực Đẩy Ác-Si-Mét Trong Đời Sống

Khí cầu cần có thể tích bao nhiêu để có thể nâng một người nặng 60 kg lên khỏi mặt đất? Biết rằng lực đẩy Ác-si-mét cần thiết phải lớn hơn tổng trọng lượng của người và khí cầu.

Lời giải:

Tính toán thể tích khí cầu dựa trên yêu cầu cân bằng lực đẩy và trọng lượng:

\[ V_x > \frac{700}{d_k - d_H} \approx 58.33 m^3 \]

4. Kết Luận

Các dạng bài tập về lực đẩy Ác-si-mét không chỉ giúp học sinh nắm vững kiến thức mà còn ứng dụng thực tế vào đời sống, từ thiết kế tàu thuyền đến sản xuất khinh khí cầu.

Lực đẩy Acsimet là một hiện tượng vật lý xảy ra khi một vật thể bị nhúng chìm trong chất lỏng (hoặc khí), và được chất lỏng tác dụng một lực đẩy hướng từ dưới lên. Lực đẩy này được đặt tên theo nhà toán học và vật lý học người Hy Lạp cổ đại, Archimedes, người đã phát hiện ra nguyên lý này.

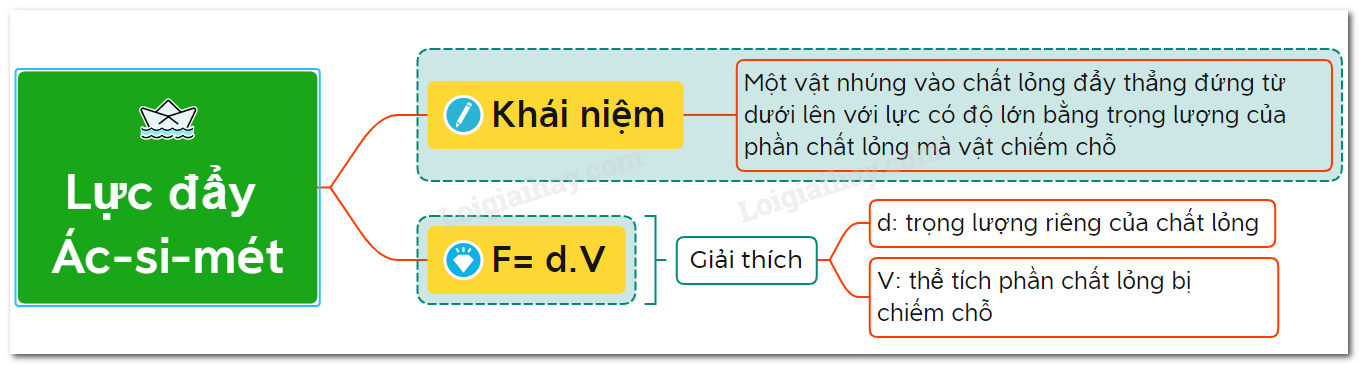
Theo nguyên lý Acsimet, "một vật thể bị nhúng chìm hoàn toàn hoặc một phần trong chất lỏng sẽ chịu một lực đẩy từ dưới lên trên có độ lớn bằng trọng lượng của phần chất lỏng bị vật chiếm chỗ."

Để tính toán lực đẩy Acsimet, ta sử dụng công thức:

\[
F_A = d \cdot V
\]

Trong đó:

• F_A: Lực đẩy Acsimet (N).
• d: Trọng lượng riêng của chất lỏng (N/m³).
• V: Thể tích phần chất lỏng bị vật chiếm chỗ (m³).

Ví dụ, khi một vật có thể tích 0,01 m³ nhúng chìm hoàn toàn trong nước có trọng lượng riêng là 10000 N/m³, lực đẩy Acsimet tác dụng lên vật sẽ là:

\[
F_A = 10000 \cdot 0,01 = 100 \, \text{N}
\]

Điều này có nghĩa là lực đẩy Acsimet sẽ làm cho vật trở nên nhẹ hơn khi ở trong chất lỏng, tạo cảm giác nổi.

Lực đẩy Acsimet không chỉ là một khái niệm lý thuyết mà còn có rất nhiều ứng dụng trong đời sống và các lĩnh vực khoa học kỹ thuật. Dưới đây là một số ứng dụng phổ biến của lực đẩy Acsimet:

2.1. Thiết Kế Tàu Thuyền

Một trong những ứng dụng rõ ràng nhất của lực đẩy Acsimet là trong thiết kế tàu thuyền. Khi tàu thuyền di chuyển trên mặt nước, nó chịu tác dụng của lực đẩy Acsimet, giúp nó nổi lên trên mặt nước thay vì chìm. Thiết kế tàu thuyền phải đảm bảo rằng trọng lượng của tàu không vượt quá lực đẩy Acsimet để tránh tàu bị chìm.

2.2. Sản Xuất Khinh Khí Cầu

Khinh khí cầu hoạt động dựa trên nguyên lý của lực đẩy Acsimet. Bên trong khinh khí cầu được bơm khí nhẹ hơn không khí bên ngoài, tạo ra một lực đẩy hướng lên trên. Lực đẩy này giúp khinh khí cầu có thể bay lên cao và duy trì sự nổi trong không khí.

2.3. Đo Trọng Lượng Và Thể Tích Vật Thể

Lực đẩy Acsimet còn được ứng dụng trong việc đo trọng lượng và thể tích của vật thể. Bằng cách nhúng một vật vào chất lỏng và đo lực đẩy Acsimet tác dụng lên vật, ta có thể tính toán thể tích của vật dựa trên sự chênh lệch trọng lượng trước và sau khi nhúng.

2.4. Ứng Dụng Trong Y Học

Trong y học, lực đẩy Acsimet được sử dụng để đo mật độ của xương và các mô mềm thông qua kỹ thuật đánh giá lực đẩy khi các bộ phận cơ thể bị nhúng trong nước. Đây là một phương pháp không xâm lấn và an toàn để kiểm tra tình trạng sức khỏe của bệnh nhân.

2.5. Thí Nghiệm Và Giảng Dạy

Lực đẩy Acsimet thường được sử dụng trong các thí nghiệm vật lý tại trường học để minh họa nguyên lý về lực đẩy trong chất lỏng. Qua các thí nghiệm này, học sinh có thể hiểu rõ hơn về cách mà lực đẩy Acsimet hoạt động, từ đó áp dụng vào giải các bài tập thực tế.

Các dạng bài tập về lực đẩy Acsimet giúp học sinh nắm vững lý thuyết và áp dụng vào giải quyết các tình huống thực tế. Dưới đây là các dạng bài tập cơ bản thường gặp trong chương trình học.

3.1. Bài Tập Tính Lực Đẩy Trên Vật Nhúng Trong Chất Lỏng

Trong dạng bài tập này, yêu cầu thường gặp là tính lực đẩy Acsimet tác dụng lên một vật khi nhúng chìm hoàn toàn trong chất lỏng. Các bước giải bao gồm:

• Xác định thể tích của vật V.
• Xác định trọng lượng riêng của chất lỏng d.
• Áp dụng công thức tính lực đẩy Acsimet: \[ F_A = d \cdot V \]

Ví dụ: Một khối kim loại có thể tích 0,02 m³ được nhúng chìm hoàn toàn trong nước có trọng lượng riêng là 10000 N/m³. Tính lực đẩy Acsimet.

3.2. Bài Tập Tính Lực Đẩy Trên Vật Nổi

Trong các bài tập về vật nổi, trọng tâm là xác định thể tích phần vật chìm trong chất lỏng để tính lực đẩy Acsimet và phân tích điều kiện nổi của vật. Các bước cơ bản:

• Xác định thể tích phần chìm của vật V_chìm.
• Tính lực đẩy Acsimet: \[ F_A = d \cdot V_{chìm} \]
• So sánh lực đẩy với trọng lượng của vật để kết luận vật nổi hay chìm.

Ví dụ: Một khối gỗ có khối lượng 5 kg nổi trên mặt nước. Xác định thể tích phần gỗ bị chìm biết trọng lượng riêng của gỗ là 6000 N/m³ và của nước là 10000 N/m³.

3.3. Bài Tập So Sánh Lực Đẩy Trên Các Vật Khác Nhau

Dạng bài tập này thường yêu cầu so sánh lực đẩy Acsimet trên các vật khác nhau nhúng trong cùng một chất lỏng, dựa vào khối lượng riêng hoặc thể tích của các vật. Các bước thực hiện:

• Tính lực đẩy Acsimet trên mỗi vật theo công thức: \[ F_{A1} = d \cdot V_{1}, \quad F_{A2} = d \cdot V_{2} \]
• So sánh các lực đẩy với nhau để xác định vật nào chịu lực đẩy lớn hơn.

Ví dụ: So sánh lực đẩy Acsimet tác dụng lên hai vật có khối lượng bằng nhau, nhưng một vật làm từ nhôm và một vật làm từ thép, khi cả hai được nhúng chìm trong nước.

Các dạng bài tập nâng cao về lực đẩy Acsimet yêu cầu người học phải kết hợp nhiều kiến thức và kỹ năng phân tích, áp dụng vào các tình huống phức tạp hơn. Dưới đây là các dạng bài tập thường gặp ở mức độ nâng cao.

4.1. Bài Tập Ứng Dụng Lực Đẩy Trong Đời Sống

Dạng bài tập này yêu cầu áp dụng kiến thức về lực đẩy Acsimet vào các tình huống thực tế, chẳng hạn như tính toán lực đẩy trên các thiết bị nổi hoặc tàu thuyền khi chịu tác động của các yếu tố ngoại cảnh như dòng chảy hoặc gió. Các bước giải bao gồm:

• Phân tích đề bài để xác định các lực tác động lên vật thể (trọng lực, lực đẩy Acsimet, lực cản).
• Tính toán các đại lượng liên quan như thể tích phần chìm, diện tích tiếp xúc với chất lỏng.
• Sử dụng các công thức vật lý để giải bài toán, chẳng hạn: \[ F_A = d \cdot V \]

4.2. Bài Tập Kết Hợp Nhiều Yếu Tố (Khối Lượng, Trọng Lượng Riêng, Thể Tích)

Trong dạng bài tập này, người học cần sử dụng đồng thời nhiều công thức để tính toán các yếu tố như khối lượng, trọng lượng riêng và thể tích. Các bước giải bao gồm:

• Đề bài thường yêu cầu tính lực đẩy Acsimet khi biết khối lượng của vật và trọng lượng riêng của chất lỏng. Công thức áp dụng: \[ F_A = d \cdot \frac{m}{d_{vật}} \]
• Tính toán thể tích của vật dựa trên khối lượng và trọng lượng riêng: \[ V = \frac{m}{d_{vật}} \]
• So sánh lực đẩy với trọng lượng để xác định trạng thái của vật (nổi, chìm, lơ lửng).

4.3. Bài Tập Tính Công Để Nhấn Chìm Hoặc Nổi Vật Trong Nước

Loại bài tập này yêu cầu tính toán công cần thiết để nhấn chìm hoặc nâng vật lên khỏi mặt nước. Các bước cơ bản bao gồm:

• Xác định lực cần thiết để nhấn chìm vật (hiệu giữa trọng lượng và lực đẩy).
• Tính công thực hiện dựa trên khoảng cách và lực tác dụng: \[ A = F \cdot s \]
• Phân tích bài toán nếu có thêm các lực tác dụng khác như lực cản, lực ma sát.

Ví dụ: Tính công cần thiết để nhấn chìm hoàn toàn một khối cầu bán kính 0,1 m có trọng lượng riêng là 5000 N/m³ vào trong nước.

Sự nổi và chìm của vật trong nước là một chủ đề quan trọng trong vật lý, đặc biệt là trong các bài tập liên quan đến lực đẩy Acsimet. Dưới đây là các dạng bài tập giúp bạn hiểu rõ hơn về hiện tượng này.

5.1. Bài Tập Xác Định Điều Kiện Nổi và Chìm

Trong dạng bài tập này, bạn cần xác định điều kiện để một vật thể nổi, chìm hoặc lơ lửng trong nước. Các bước cơ bản bao gồm:

• Xác định trọng lượng riêng của vật d_vật và của nước d_nước.
• So sánh hai trọng lượng riêng:
  • Nếu \(d_{vật} > d_{nước}\), vật sẽ chìm.
  • Nếu \(d_{vật} < d_{nước}\), vật sẽ nổi.
  • Nếu \(d_{vật} = d_{nước}\), vật sẽ lơ lửng.

Ví dụ: Một vật có trọng lượng riêng là 8000 N/m³ được thả vào nước. Hãy xác định trạng thái của vật.

5.2. Bài Tập Tính Thể Tích Phần Chìm Của Vật Nổi

Dạng bài tập này yêu cầu bạn tính thể tích phần chìm của vật khi nó nổi trên mặt nước. Các bước cơ bản:

• Xác định trọng lượng của vật P và lực đẩy Acsimet F_A.
• Sử dụng công thức cân bằng lực: \[ F_A = P \]
• Từ đó tính thể tích phần chìm: \[ V_{chìm} = \frac{P}{d_{nước}} \]

Ví dụ: Một vật có trọng lượng 20 N được thả nổi trên nước. Tính thể tích phần chìm của vật, biết trọng lượng riêng của nước là 10000 N/m³.

5.3. Bài Tập Tính Trọng Lượng Riêng Của Vật Dựa Trên Độ Nổi

Trong các bài tập này, bạn sẽ tính trọng lượng riêng của vật dựa trên độ nổi hoặc chìm của vật trong nước. Các bước giải:

• Đo thể tích phần chìm V_chìm và toàn bộ thể tích của vật V.
• Tính trọng lượng riêng của vật: \[ d_{vật} = d_{nước} \cdot \frac{V_{chìm}}{V} \]

Ví dụ: Một khối gỗ có thể tích 0,5 m³, trong đó 0,3 m³ bị chìm trong nước. Tính trọng lượng riêng của gỗ, biết trọng lượng riêng của nước là 10000 N/m³.

5.4. Bài Tập Tính Công Để Kéo Vật Chìm Lên

Loại bài tập này liên quan đến việc tính toán công cần thiết để kéo một vật từ đáy hồ lên mặt nước. Các bước thực hiện:

• Tính lực kéo cần thiết để thắng lực đẩy Acsimet và trọng lượng của vật.
• Sử dụng công thức tính công: \[ A = F \cdot s \]

Ví dụ: Tính công cần thiết để kéo một khối kim loại nặng 50 N từ đáy hồ lên mặt nước, biết lực đẩy Acsimet tác dụng lên vật là 20 N.

Thể tích chất lỏng bị vật chiếm chỗ là một khía cạnh quan trọng trong việc hiểu rõ nguyên lý lực đẩy Acsimet. Dưới đây là các dạng bài tập giúp bạn rèn luyện kỹ năng tính toán và hiểu biết về hiện tượng này.

6.1. Bài Tập Tính Thể Tích Chất Lỏng Bị Chiếm Chỗ Khi Vật Nhúng Chìm Hoàn Toàn

Trong dạng bài tập này, mục tiêu là tính thể tích chất lỏng bị chiếm chỗ khi một vật được nhúng chìm hoàn toàn trong chất lỏng. Các bước thực hiện:

• Xác định thể tích của vật V_vật.
• Áp dụng nguyên lý của lực đẩy Acsimet: Thể tích chất lỏng bị chiếm chỗ bằng với thể tích của vật nhúng chìm hoàn toàn.
• Kết luận: \[ V_{chất\ lỏng} = V_{vật} \]

Ví dụ: Một khối gỗ có thể tích 0,05 m³ được nhúng chìm hoàn toàn trong nước. Tính thể tích nước bị khối gỗ chiếm chỗ.

6.2. Bài Tập Tính Thể Tích Chất Lỏng Bị Chiếm Chỗ Khi Vật Nổi Một Phần

Ở dạng bài tập này, bạn sẽ tính thể tích chất lỏng bị chiếm chỗ khi vật chỉ nổi một phần trên mặt nước. Các bước bao gồm:

• Tính toán thể tích phần chìm của vật dựa trên lực đẩy Acsimet và trọng lượng của vật.
• Xác định thể tích chất lỏng bị chiếm chỗ, tức là thể tích phần chìm của vật: \[ V_{chất\ lỏng} = V_{chìm} \]

Ví dụ: Một chiếc phao hình cầu có khối lượng 2 kg nổi trên mặt nước, một nửa thể tích của phao bị chìm. Tính thể tích nước bị phao chiếm chỗ, biết thể tích toàn bộ phao là 0,04 m³.

6.3. Bài Tập Xác Định Thể Tích Chất Lỏng Khi Vật Có Hình Dạng Phức Tạp

Dạng bài tập này yêu cầu tính thể tích chất lỏng bị chiếm chỗ khi vật có hình dạng không đều hoặc phức tạp. Các bước giải:

• Sử dụng phương pháp chia nhỏ vật thể thành các hình khối đơn giản (hình hộp, hình trụ, v.v.) để tính toán thể tích.
• Tính tổng thể tích của các phần để xác định thể tích chất lỏng bị chiếm chỗ.

Ví dụ: Một khối vật thể có hình dạng phức tạp được tạo thành từ một khối lập phương cạnh 0,2 m và một hình trụ bán kính 0,1 m, cao 0,3 m. Tính thể tích chất lỏng bị vật chiếm chỗ khi nó được nhúng chìm hoàn toàn.

6.4. Bài Tập Liên Quan Đến Sự Thay Đổi Mực Nước Khi Vật Chiếm Chỗ

Loại bài tập này yêu cầu tính toán sự thay đổi mực nước khi một vật được thả vào một bể chứa nước. Các bước thực hiện:

• Xác định diện tích đáy của bể chứa A.
• Tính thể tích chất lỏng bị vật chiếm chỗ và từ đó xác định mức tăng của mực nước: \[ \Delta h = \frac{V_{vật}}{A} \]

Ví dụ: Một vật có thể tích 0,01 m³ được thả vào bể nước có diện tích đáy là 2 m². Tính độ tăng mực nước trong bể.