Định Nghĩa Momen Lực - Hiểu Rõ Khái Niệm Cốt Lõi và Ứng Dụng Thực Tiễn

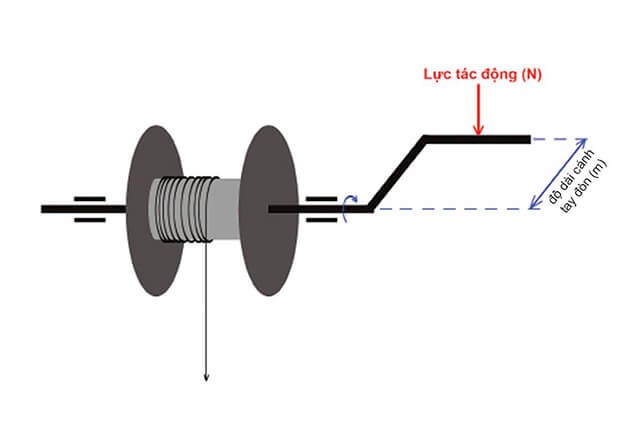
Momen lực, hay còn gọi là mômen xoắn, là một khái niệm quan trọng trong vật lý học và cơ học. Momen lực được hiểu là đại lượng thể hiện sự quay của một vật thể xung quanh một điểm hoặc trục cố định dưới tác động của lực.

Công Thức Tính Momen Lực

Momen lực được tính bằng công thức:

$M\; =\; F\; \backslash times\; d$

Trong đó:

• $M$: Momen lực (đơn vị: Newton mét, ký hiệu: N.m)
• $F$: Lực tác dụng lên vật (đơn vị: Newton, ký hiệu: N)
• $d$: Khoảng cách từ điểm quay đến đường tác dụng của lực (đơn vị: mét)

Quy Tắc Momen Lực

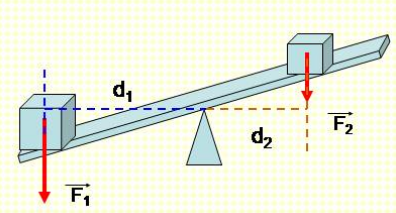
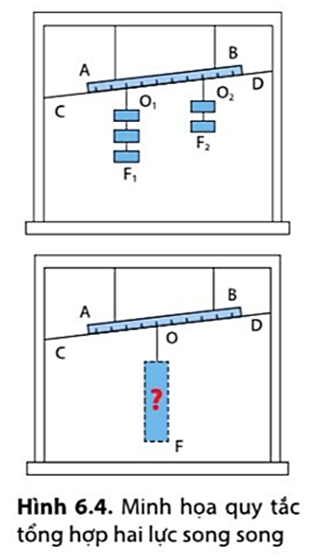
Quy tắc momen lực cho biết rằng nếu tổng các momen lực tác dụng lên một vật thể bằng 0, vật thể sẽ cân bằng và không quay. Ngược lại, nếu có momen lực khác không, vật thể sẽ quay quanh điểm hoặc trục cố định.

Ứng Dụng Của Momen Lực

• Trong cơ khí: Momen lực được áp dụng trong thiết kế và chế tạo các hệ thống cơ khí, chẳng hạn như cần trục, đòn bẩy, hay bánh răng.
• Trong thể thao: Hiểu biết về momen lực giúp cải thiện kỹ thuật và hiệu suất trong các môn thể thao như golf, quần vợt, và bóng đá.
• Trong robot học: Tính toán và kiểm soát momen lực là yếu tố quan trọng để đảm bảo rằng robot có thể thực hiện các nhiệm vụ một cách chính xác và ổn định.

Tính Chất Của Momen Lực

Momen lực có hai tính chất quan trọng:

• Hướng: Momen lực có hướng xác định, thường được biểu diễn bằng một vectơ.
• Tính cộng: Các momen lực có thể được cộng lại để tính tổng momen lực tác dụng lên vật thể.

Momen lực, còn được gọi là mômen xoắn, là một đại lượng vật lý thể hiện khả năng của một lực làm quay một vật quanh một trục hoặc một điểm cố định. Trong đời sống hàng ngày, momen lực có thể được hiểu là khả năng xoay của một cánh cửa khi ta tác dụng lực vào tay nắm cửa.

Momen lực được tính bằng công thức:

$M\; =\; F\; \backslash times\; d$

Trong đó:

• $M$: Momen lực (đơn vị: Newton mét, ký hiệu: N.m)
• $F$: Lực tác dụng lên vật (đơn vị: Newton, ký hiệu: N)
• $d$: Khoảng cách từ điểm đặt lực đến trục quay (đơn vị: mét, ký hiệu: m)

Công thức trên cho thấy rằng momen lực không chỉ phụ thuộc vào lực tác dụng, mà còn phụ thuộc vào khoảng cách từ điểm đặt lực đến trục quay. Khoảng cách càng lớn thì momen lực càng lớn, đồng nghĩa với việc vật dễ dàng quay hơn.

Ví dụ thực tế, khi bạn mở cửa, nếu bạn tác dụng lực càng xa bản lề thì cửa sẽ càng dễ mở. Đây chính là minh họa cơ bản của momen lực trong cuộc sống hàng ngày.

Momen lực cũng tuân theo nguyên tắc cộng lực, có nghĩa là tổng momen lực tác dụng lên một vật sẽ là tổng của các momen lực riêng lẻ. Nếu tổng momen lực bằng không, vật sẽ ở trạng thái cân bằng và không quay.

Để hiểu rõ hơn về momen lực, hãy xem xét một số ví dụ và bài tập thực tế. Những ví dụ này sẽ giúp bạn nắm bắt cách tính toán momen lực và ứng dụng vào các tình huống cụ thể.

• Ví dụ 1: Một lực \( F = 50 \, N \) tác dụng vuông góc lên một cánh tay đòn dài \( d = 2 \, m \) từ trục quay. Tính momen lực.
• Giải: Momen lực \( M \) được tính bằng công thức \( M = F \times d \). Thay giá trị vào, ta có: \( M = 50 \, N \times 2 \, m = 100 \, Nm \).

• Ví dụ 2: Một cửa xoay cần một lực \( F = 30 \, N \) để mở, với khoảng cách từ tay cầm đến trục quay là \( d = 1.5 \, m \). Tính momen lực cần thiết để mở cửa.
• Giải: Áp dụng công thức \( M = F \times d \), ta có: \( M = 30 \, N \times 1.5 \, m = 45 \, Nm \).

• Bài tập 1: Tính momen lực khi một lực \( F = 70 \, N \) tác dụng lên một cần gạt dài \( d = 3 \, m \) từ trục quay. Lực này tác dụng một góc \( 60^\circ \) so với cánh tay đòn.
• Đáp án gợi ý: Momen lực trong trường hợp này sẽ là \( M = F \times d \times \sin(\theta) \).

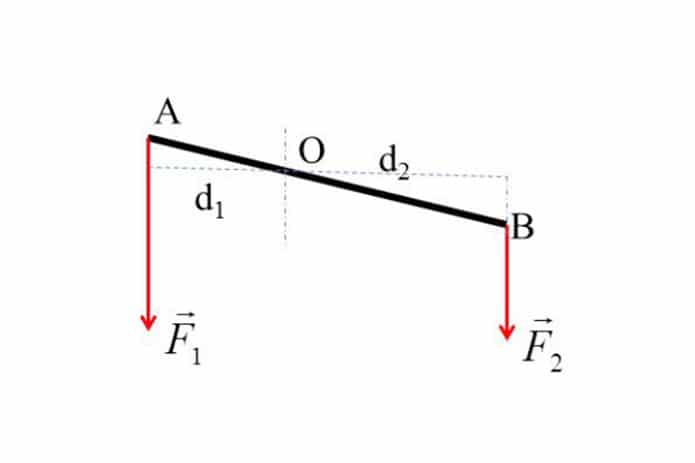
• Bài tập 2: Một thanh chắn dài \( 5 \, m \) với trục quay ở giữa, một lực \( F_1 = 40 \, N \) tác dụng lên đầu trái của thanh, và lực \( F_2 = 60 \, N \) tác dụng lên đầu phải. Tính tổng momen lực và xác định chiều quay của thanh chắn.
• Đáp án gợi ý: Xác định momen lực cho từng lực tác dụng và cộng các momen lại để có tổng momen lực.

Các ví dụ và bài tập trên sẽ giúp bạn luyện tập và hiểu sâu hơn về khái niệm momen lực trong cơ học.

Momen lực là một khái niệm cơ bản và quan trọng trong cơ học, giúp chúng ta hiểu rõ hơn về cách lực tác dụng lên các vật thể và tạo ra chuyển động quay. Việc nắm vững quy tắc momen lực không chỉ giúp chúng ta giải quyết các bài toán trong vật lý mà còn áp dụng hiệu quả vào đời sống hàng ngày, từ việc mở cửa đến vận hành các thiết bị cơ học phức tạp. Hãy tiếp tục khám phá và ứng dụng kiến thức này để đạt được những kết quả tốt nhất trong học tập và công việc.