Momen Lực Công Thức: Cách Tính Toán Và Ứng Dụng Thực Tiễn

Momen lực là một đại lượng vật lý quan trọng trong việc xác định khả năng quay của một vật quanh một trục cố định dưới tác dụng của lực. Công thức tính momen lực được sử dụng trong nhiều lĩnh vực như cơ khí, kỹ thuật xây dựng, và các ứng dụng công nghiệp khác.

Công Thức Tính Momen Lực

Công thức cơ bản để tính momen lực (M) được biểu diễn như sau:

\[ M = F \cdot d \]

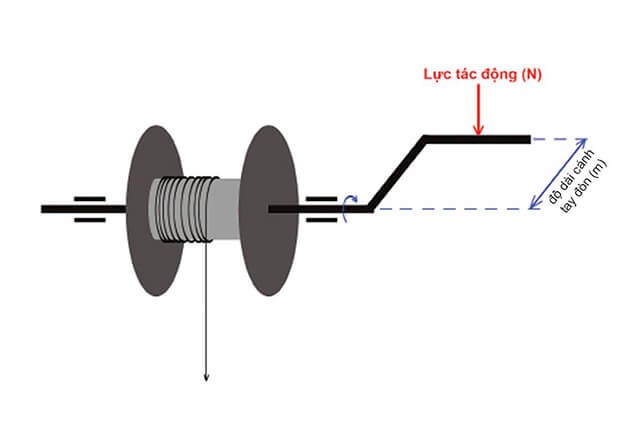
• F: Độ lớn của lực tác dụng (đơn vị: Newton - N)
• d: Khoảng cách từ trục quay đến giá đỡ của lực (đơn vị: mét - m), thường gọi là "tay đòn" của lực.
• M: Momen lực (đơn vị: Newton mét - Nm)

Quy Tắc Momen Lực

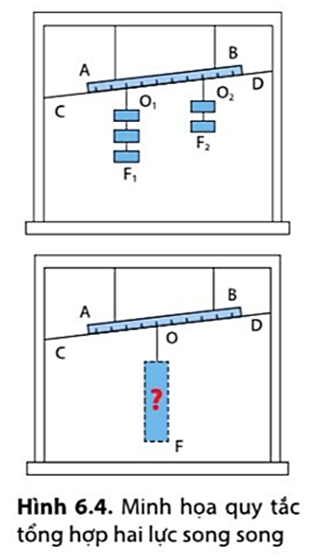
Quy tắc momen lực được áp dụng để xác định điều kiện cân bằng của một vật có trục quay cố định. Để vật ở trạng thái cân bằng, tổng momen lực làm vật quay theo chiều kim đồng hồ phải bằng tổng momen lực làm vật quay ngược chiều kim đồng hồ.

\[ \sum M_{clockwise} = \sum M_{counterclockwise} \]

Ứng Dụng Của Momen Lực

• Cơ Khí: Momen lực được sử dụng trong thiết kế máy móc, đặc biệt là trong các hệ thống đòn bẩy, bánh răng, và động cơ.
• Thể Thao: Trong các môn thể thao như bóng đá, golf, và quần vợt, hiểu biết về momen lực giúp cải thiện kỹ thuật và hiệu suất của vận động viên.
• Robot Học: Momen lực đóng vai trò quan trọng trong việc điều khiển và vận hành các cánh tay robot, đảm bảo độ chính xác và ổn định.
• Xây Dựng: Trong ngành xây dựng, tính toán momen lực giúp đảm bảo an toàn và độ bền của các công trình.

Bài Tập Về Momen Lực

Dưới đây là một số bài tập giúp bạn luyện tập và hiểu rõ hơn về momen lực:

1. Một thanh kim loại có chiều dài l khối lượng m đặt trên bàn nhô ra một đoạn bằng 1/4 chiều dài thanh. Tác dụng lực có độ lớn 40N hướng xuống thì đầu kia của thanh kim loại bắt đầu nhô lên. Tính khối lượng của thanh kim loại.
2. Một thanh AB nặng 30 kg, dài 9 m, trọng tâm tại G. Người ta phải tác dụng vào đầu B một lực F=100 N. Xác định độ lớn của lực tác dụng vào trục quay để thanh nằm cân bằng.
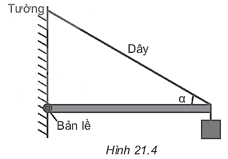
3. Một thanh gỗ nặng 12 kg dài 1,5 m, một đầu được gắn cố định đi qua điểm A. Tính lực căng của sợi dây và lực tác dụng tại điểm A của thanh gỗ.

Việc nắm vững công thức và quy tắc momen lực là nền tảng quan trọng giúp bạn giải quyết các bài toán cơ học trong thực tế một cách hiệu quả và chính xác.

Momen lực là một khái niệm quan trọng trong cơ học, liên quan đến sự quay của vật thể xung quanh một trục cố định khi bị tác dụng bởi lực. Đây là đại lượng mô tả khả năng làm cho vật quay, với giá trị phụ thuộc vào lực tác dụng và khoảng cách từ trục quay đến điểm tác dụng lực.

Trong thực tế, momen lực được sử dụng để phân tích và giải quyết nhiều bài toán liên quan đến sự cân bằng và chuyển động quay của các vật thể. Dưới đây là một số điểm chính về momen lực:

• Khái niệm: Momen lực là sản phẩm của lực và tay đòn, được tính bằng công thức \[ M = F \times d \], trong đó:
  • F: Lực tác dụng (Newton - N)
  • d: Khoảng cách từ trục quay đến điểm tác dụng lực (mét - m)
• Đơn vị: Momen lực có đơn vị là Newton mét (Nm), biểu thị sức mạnh của lực khi làm cho vật quay quanh trục.
• Ứng dụng: Momen lực xuất hiện trong nhiều lĩnh vực như cơ khí, xây dựng, và điện tử, đặc biệt trong việc thiết kế máy móc và hệ thống cơ học.

Hiểu rõ về momen lực và công thức tính toán giúp chúng ta áp dụng vào các bài toán thực tế và tối ưu hóa các hệ thống cơ học trong sản xuất và đời sống hàng ngày.

Công thức tính momen lực được sử dụng để xác định khả năng tạo ra chuyển động quay của một vật thể dưới tác dụng của lực. Công thức tổng quát cho momen lực được biểu diễn như sau:

\[ M = F \times d \]

Trong đó:

• \(M\): Momen lực (đơn vị: Newton mét - Nm)
• \(F\): Lực tác dụng lên vật thể (đơn vị: Newton - N)
• \(d\): Khoảng cách từ trục quay đến điểm tác dụng của lực, còn được gọi là tay đòn (đơn vị: mét - m)

Để tính toán momen lực một cách chính xác, ta cần xác định các yếu tố sau:

1. Đo lực tác dụng \(F\): Sử dụng các thiết bị đo lực để xác định giá trị lực tác dụng lên vật thể.
2. Xác định tay đòn \(d\): Đo khoảng cách từ trục quay đến điểm tác dụng của lực trên vật thể.
3. Áp dụng công thức: Nhân lực \(F\) với tay đòn \(d\) để tính toán giá trị momen lực \(M\).

Công thức này đơn giản nhưng rất hữu ích trong nhiều lĩnh vực, đặc biệt là trong cơ khí và kỹ thuật xây dựng, nơi các hệ thống đòn bẩy và bánh răng được sử dụng rộng rãi.

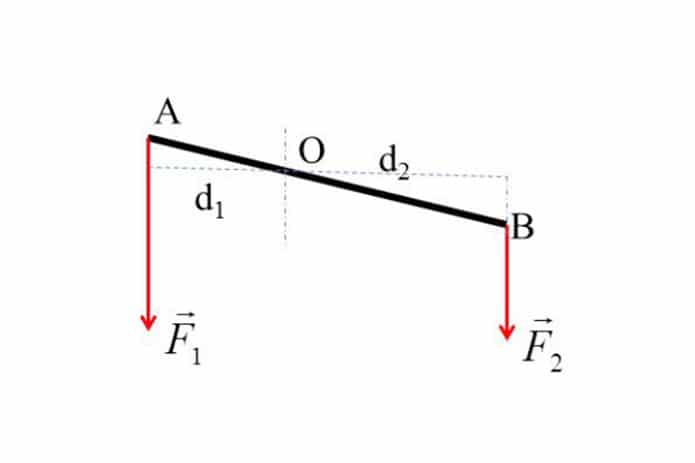
Quy tắc momen lực là nguyên tắc cơ bản trong cơ học để xác định cân bằng của một vật thể quay. Quy tắc này phát biểu rằng một vật sẽ ở trạng thái cân bằng nếu tổng momen lực tác dụng lên nó bằng 0. Để áp dụng quy tắc này, ta cần tuân thủ các bước sau:

1. Xác định trục quay: Chọn một điểm hoặc đường thẳng mà vật quay xung quanh.
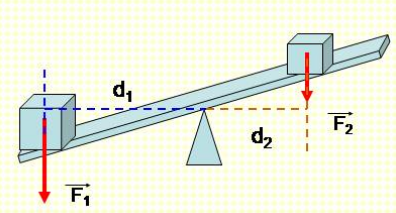
2. Tính momen lực cho từng lực tác dụng: Sử dụng công thức \( M = F \times d \) để tính momen lực của từng lực tác dụng lên vật. Chú ý đến hướng của lực để xác định chiều quay (chiều thuận hoặc chiều nghịch).
3. Áp dụng quy tắc momen: Tổng momen lực theo chiều thuận phải bằng tổng momen lực theo chiều nghịch để vật cân bằng. Tức là: \[ \sum M_{\text{thuận}} = \sum M_{\text{nghịch}} \]
4. Kiểm tra và điều chỉnh: Nếu không đạt được cân bằng, điều chỉnh các lực hoặc thay đổi khoảng cách để đạt trạng thái cân bằng.

Quy tắc momen lực được áp dụng rộng rãi trong thiết kế các hệ thống cơ khí, như đòn bẩy, cầu cân, và trong nhiều ứng dụng kỹ thuật khác để đảm bảo rằng các hệ thống hoạt động một cách ổn định và hiệu quả.

Momen lực là khái niệm quan trọng trong vật lý và cơ học, với nhiều ứng dụng thực tế trong đời sống và công nghiệp. Dưới đây là một số ứng dụng chính của momen lực:

• Thiết kế đòn bẩy: Đòn bẩy là công cụ cơ bản dựa trên nguyên lý momen lực. Khi áp dụng lực ở một đầu của đòn bẩy, momen lực tạo ra có thể nâng hoặc di chuyển các vật nặng một cách dễ dàng hơn.
• Quá trình quay của động cơ: Trong các động cơ, momen lực đóng vai trò chính trong việc tạo ra mô-men xoắn, giúp các trục động cơ quay, từ đó vận hành các thiết bị cơ khí.
• Cầu cân và thang đo: Các hệ thống cân và đo lường sử dụng nguyên tắc momen lực để xác định trọng lượng của vật. Bằng cách cân bằng momen lực ở hai bên của cầu cân, ta có thể xác định khối lượng của vật cần đo.
• Thiết kế kết cấu xây dựng: Trong xây dựng, momen lực được tính toán kỹ lưỡng để đảm bảo các kết cấu như dầm, cột có thể chịu lực một cách an toàn và ổn định, tránh tình trạng đổ sập.
• Các dụng cụ cầm tay: Momen lực cũng được ứng dụng trong các dụng cụ cầm tay như tua vít, mỏ lết, nơi cần tính toán lực xoắn phù hợp để vặn các ốc vít hoặc bu lông.

Các ứng dụng của momen lực không chỉ giới hạn ở những ví dụ trên mà còn mở rộng trong nhiều lĩnh vực khác như kỹ thuật ô tô, hàng không, và trong các nghiên cứu khoa học. Việc hiểu và áp dụng đúng momen lực giúp tối ưu hóa hiệu suất và an toàn trong các hoạt động sản xuất và đời sống hàng ngày.

Dưới đây là một số bài tập về momen lực giúp bạn củng cố và áp dụng các kiến thức đã học. Hãy đọc kỹ đề bài và thử giải các bài tập theo từng bước:

• Bài tập 1: Một đòn bẩy có chiều dài 2m, với điểm tựa nằm ở giữa. Khi một lực F = 100N tác dụng vào một đầu của đòn bẩy, hãy tính momen lực tác dụng lên điểm tựa.

Hướng dẫn:

1. Xác định khoảng cách từ điểm tác dụng lực đến điểm tựa, ở đây là 1m.
2. Sử dụng công thức tính momen lực: \[ M = F \times d \]
   Trong đó, \( M \) là momen lực, \( F \) là lực tác dụng, và \( d \) là khoảng cách từ điểm tác dụng lực đến điểm tựa.
3. Thay số vào công thức: \[ M = 100N \times 1m = 100Nm \]
   Vậy momen lực tác dụng lên điểm tựa là 100Nm.
• Bài tập 2: Một vật nặng có khối lượng 50kg được treo ở một đầu của thanh ngang dài 3m. Hãy tính momen lực mà vật nặng này tạo ra quanh điểm tựa ở đầu kia của thanh ngang.

Hướng dẫn:

1. Đầu tiên, tính trọng lực tác dụng lên vật nặng: \[ F = m \times g = 50kg \times 9.8m/s^2 = 490N \]
2. Khoảng cách từ vật nặng đến điểm tựa là 3m.
3. Sử dụng công thức momen lực: \[ M = F \times d = 490N \times 3m = 1470Nm \]
4. Vậy momen lực mà vật nặng tạo ra là 1470Nm.

Việc thực hành giải các bài tập về momen lực sẽ giúp bạn nắm vững lý thuyết và áp dụng một cách linh hoạt vào các tình huống thực tế.