Chủ đề quy tắc momen lực trắc nghiệm: Quy tắc momen lực trắc nghiệm là một phần quan trọng trong học tập vật lý, giúp bạn hiểu rõ cách tính toán và áp dụng momen lực vào các bài toán thực tế. Bài viết này cung cấp hướng dẫn chi tiết, cùng với các bài tập trắc nghiệm giúp củng cố kiến thức và kỹ năng của bạn.
Mục lục
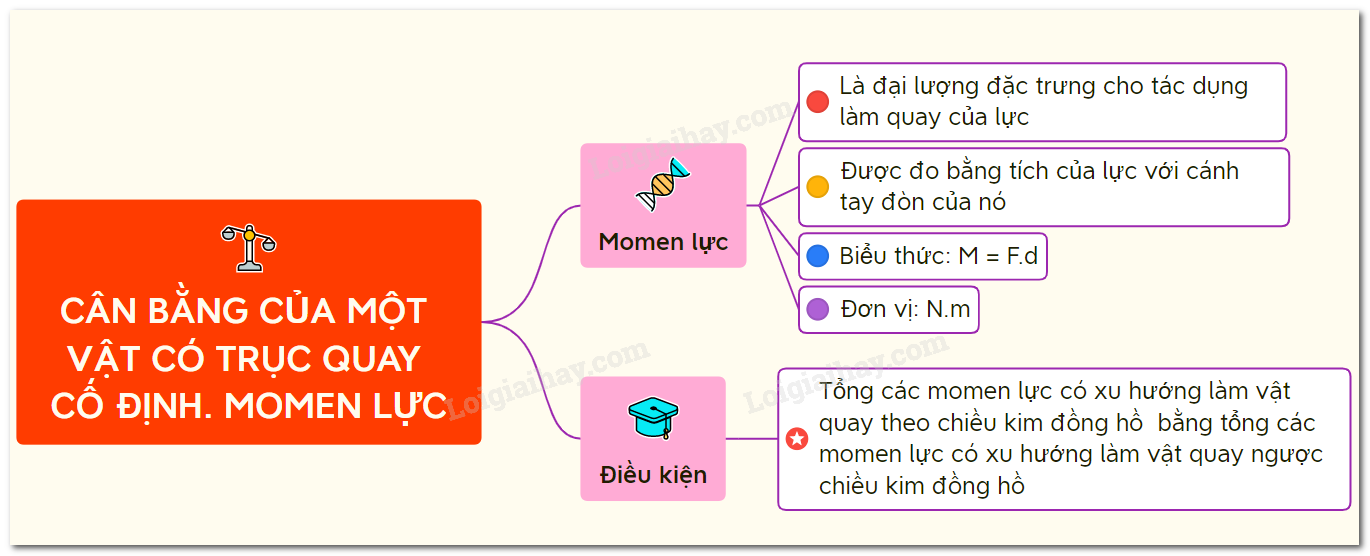
Quy Tắc Momen Lực: Khái Niệm và Ứng Dụng
Quy tắc momen lực là một trong những nguyên tắc cơ bản của cơ học, thường được áp dụng trong các bài toán liên quan đến sự cân bằng và chuyển động quay. Quy tắc này được sử dụng để tính toán và phân tích momen lực của các lực tác dụng lên một vật thể có trục quay cố định.
Điều Kiện Cân Bằng
Để một vật thể có trục quay cố định nằm cân bằng, tổng momen của các lực tác dụng lên vật phải bằng 0:
\[ \sum \vec{M} = 0 \]
Trong đó, momen của một lực được tính bằng tích của lực đó với khoảng cách từ trục quay đến giá của lực:
\[ M = F \cdot d \]
Các Bước Giải Bài Toán Momen Lực
Xác định trục quay của vật thể.
Xác định các lực tác dụng lên vật và vị trí tác dụng của chúng.
Tính toán momen lực của từng lực đối với trục quay.
Áp dụng quy tắc momen lực để thiết lập phương trình cân bằng:
\[ \sum M_{\text{clockwise}} = \sum M_{\text{counterclockwise}} \]Giải phương trình để tìm ra giá trị cần thiết.
Ví Dụ Về Quy Tắc Momen Lực
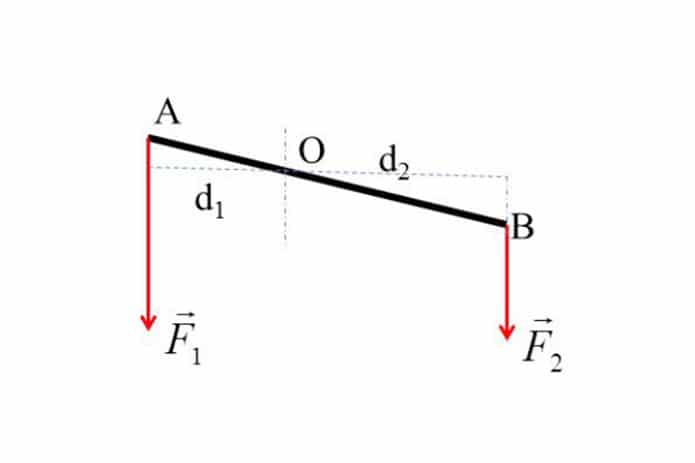
Giả sử chúng ta có một thanh AB dài 1m, điểm A được cố định và điểm B chịu tác dụng của lực \( F = 10N \) vuông góc với thanh. Khi đó, momen lực của lực này quanh điểm A là:
\[ M = F \cdot d = 10N \cdot 1m = 10Nm \]
Bài Tập Trắc Nghiệm Về Momen Lực
Dưới đây là một số câu hỏi trắc nghiệm thường gặp liên quan đến quy tắc momen lực:
Momen lực của một vật là đại lượng đặc trưng cho:
A. Tác dụng làm quay của lực.
B. Vectơ.
C. Độ lớn của lực tác dụng.
D. Luôn có giá trị âm.
Đáp án: A
Điều kiện cân bằng của một chất điểm có trục quay cố định còn được gọi là:
A. Quy tắc hợp lực đồng quy.
B. Quy tắc hợp lực song song.
C. Quy tắc hình bình hành.
D. Quy tắc momen lực.
Đáp án: D
Một lực có độ lớn 10N tác dụng lên một vật rắn quay quanh một trục cố định, biết khoảng cách từ giá của lực đến trục quay là 20cm. Momen của lực tác dụng lên vật là:
A. 200N.m
B. 200N/m
C. 2N.m
D. 2N/m
Đáp án: C
Ứng Dụng Thực Tế Của Quy Tắc Momen Lực
Quy tắc momen lực không chỉ là một phần quan trọng trong các bài toán cơ học mà còn được áp dụng rộng rãi trong thực tế, từ việc cân bằng trên đòn bẩy, thiết kế cơ cấu máy móc cho đến việc giải quyết các vấn đề kỹ thuật trong xây dựng và sản xuất.

.png)
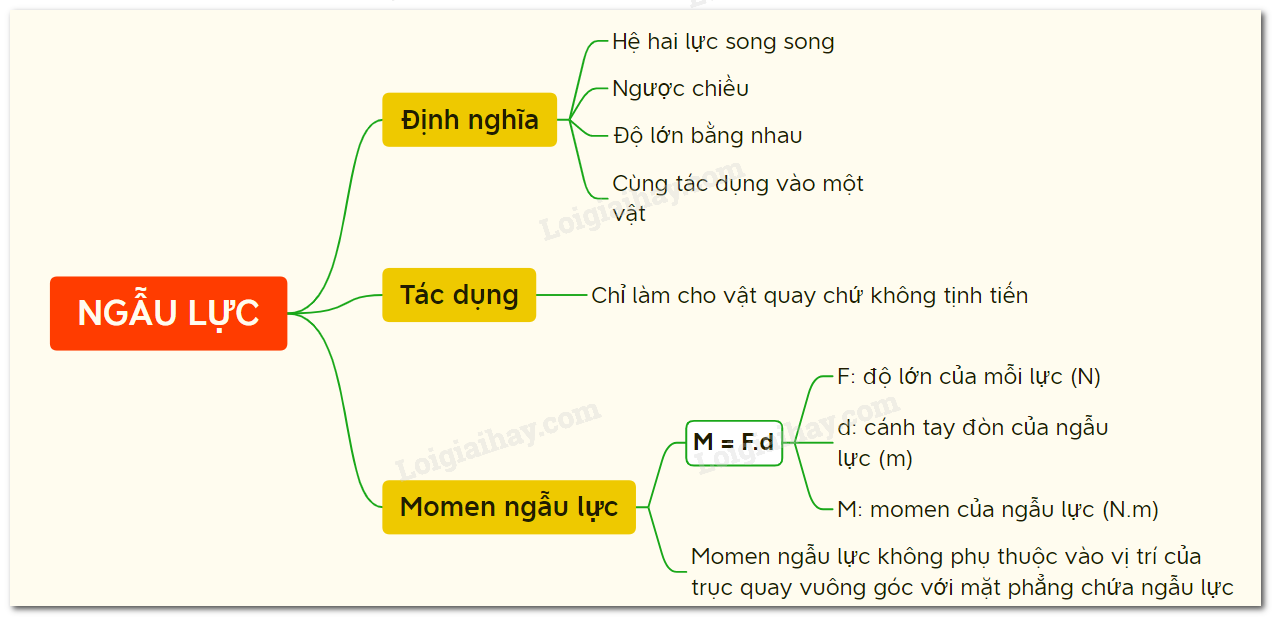
Giới thiệu về Momen Lực
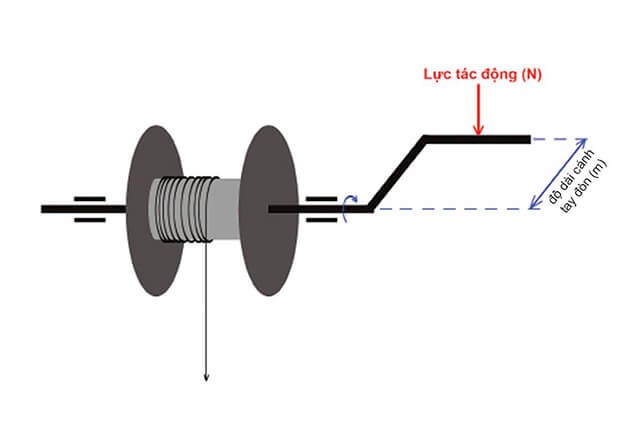
Momen lực là một khái niệm cơ bản trong cơ học, liên quan đến tác dụng làm quay của lực đối với một vật thể quanh một trục cố định. Đây là đại lượng đặc trưng cho khả năng gây ra chuyển động quay của một lực khi tác dụng lên một vật thể.
Momen lực được tính bằng tích của độ lớn của lực và khoảng cách từ trục quay đến điểm tác dụng của lực. Công thức chung của momen lực được biểu diễn như sau:
\[ M = F \cdot d \]
Trong đó:
- M: Momen lực (Newton-mét, Nm)
- F: Độ lớn của lực tác dụng (Newton, N)
- d: Khoảng cách từ trục quay đến điểm đặt lực (mét, m)
Momen lực có thể gây ra hai loại chuyển động chính: chuyển động quay thuận chiều kim đồng hồ và chuyển động quay ngược chiều kim đồng hồ. Trong bài toán cân bằng, tổng momen lực tác dụng lên một vật thể phải bằng không để vật thể duy trì trạng thái cân bằng.
Để hiểu rõ hơn về momen lực và cách nó ảnh hưởng đến các hệ thống cơ học, chúng ta cần nghiên cứu các nguyên tắc cơ bản và các ví dụ ứng dụng trong thực tế, như đòn bẩy, cánh tay đòn và bánh xe.
Quy Tắc Momen Lực
Quy tắc momen lực là một trong những nguyên tắc cơ bản trong cơ học, được sử dụng để xác định điều kiện cân bằng của một vật thể chịu tác dụng của nhiều lực. Quy tắc này phát biểu rằng: "Tổng momen lực tác dụng lên một vật quanh một trục cố định bằng 0 khi vật ở trạng thái cân bằng."
Để áp dụng quy tắc momen lực vào bài toán, ta thực hiện theo các bước sau:
Xác định trục quay: Trước tiên, ta cần xác định trục quay của vật thể, nơi mà các momen lực sẽ được tính toán.
Tính toán momen lực của từng lực: Mỗi lực tác dụng lên vật thể sẽ tạo ra một momen lực quanh trục quay. Momen lực của một lực được tính bằng công thức:
\[ M = F \cdot d \]- F: Độ lớn của lực tác dụng.
- d: Khoảng cách từ trục quay đến đường tác dụng của lực.
Xác định chiều của momen lực: Xác định momen lực quay theo chiều kim đồng hồ hay ngược chiều kim đồng hồ. Thường quy ước chiều kim đồng hồ là dương và ngược chiều kim đồng hồ là âm.
Lập phương trình cân bằng momen: Theo quy tắc momen lực, tổng các momen lực quay thuận chiều bằng tổng các momen lực quay ngược chiều khi vật thể ở trạng thái cân bằng:
\[ \sum M_{\text{clockwise}} = \sum M_{\text{counterclockwise}} \]Từ đó, ta có thể giải phương trình để tìm giá trị cần thiết, như lực tác dụng hoặc khoảng cách.
Quy tắc momen lực không chỉ áp dụng cho các bài toán đơn giản mà còn được sử dụng rộng rãi trong các bài toán cơ học phức tạp, từ việc tính toán lực trong các hệ thống cơ khí cho đến phân tích lực trong kết cấu xây dựng.

Ứng Dụng Thực Tế Của Momen Lực
Momen lực không chỉ là một khái niệm lý thuyết trong vật lý mà còn có nhiều ứng dụng thực tế trong cuộc sống hàng ngày và trong các ngành công nghiệp khác nhau. Dưới đây là một số ví dụ cụ thể về cách momen lực được ứng dụng trong thực tế:
Đòn bẩy: Đòn bẩy là một trong những ứng dụng cổ điển nhất của momen lực. Khi bạn sử dụng một thanh đòn để nâng một vật nặng, bạn đang áp dụng momen lực để tạo ra một lực lớn hơn tại điểm đầu ra. Điều này giúp giảm bớt công sức cần thiết để nâng vật.
Cờ lê và mỏ lết: Khi sử dụng cờ lê hoặc mỏ lết để vặn bu lông hoặc ốc vít, bạn đang sử dụng nguyên lý của momen lực. Càng dài tay cầm của cờ lê, lực tác động lên bu lông càng lớn, giúp dễ dàng vặn hoặc tháo các chi tiết.
Ghế bập bênh: Trong trường hợp của ghế bập bênh, momen lực được tạo ra bởi trọng lượng của người ngồi ở hai đầu của ghế. Ghế sẽ cân bằng khi tổng các momen lực tác dụng tại điểm giữa bằng không, giúp ghế duy trì trạng thái ổn định.
Thiết kế cầu và kết cấu xây dựng: Trong kỹ thuật xây dựng, momen lực đóng vai trò quan trọng trong việc thiết kế các cầu, tòa nhà và các cấu trúc khác. Kỹ sư cần tính toán momen lực để đảm bảo rằng các cấu trúc có thể chịu được lực tác động mà không bị gãy hoặc sụp đổ.
Bánh xe và trục: Khi quay một bánh xe quanh trục, momen lực được tạo ra do lực tác dụng tại bề mặt bánh xe. Điều này giúp chuyển đổi lực quay thành chuyển động thẳng, như trong các phương tiện di chuyển như xe đạp và ô tô.
Các hệ thống cơ khí trong công nghiệp: Momen lực được áp dụng rộng rãi trong các hệ thống cơ khí, từ máy móc sản xuất cho đến các thiết bị nâng hạ. Việc sử dụng đúng momen lực giúp tối ưu hóa hiệu suất và độ an toàn của hệ thống.
Những ứng dụng trên chỉ là một số ví dụ phổ biến về cách momen lực được sử dụng trong thực tế. Sự hiểu biết và áp dụng đúng nguyên lý momen lực không chỉ giúp chúng ta giải quyết các vấn đề trong kỹ thuật mà còn giúp cải thiện hiệu quả và độ an toàn trong các hoạt động hàng ngày.

Kết Luận
Qua bài viết này, chúng ta đã khám phá sâu về quy tắc momen lực, từ các khái niệm cơ bản đến ứng dụng thực tế và các bài tập trắc nghiệm. Momen lực không chỉ là một phần quan trọng trong chương trình học mà còn có nhiều ứng dụng trong đời sống và công nghiệp. Việc nắm vững quy tắc này giúp chúng ta hiểu rõ hơn về cách các vật thể vận hành trong môi trường tự nhiên và cách chúng ta có thể áp dụng kiến thức này để giải quyết các vấn đề kỹ thuật và nâng cao hiệu suất trong các hoạt động hàng ngày.
Việc thực hành thông qua các bài tập trắc nghiệm không chỉ giúp củng cố kiến thức mà còn rèn luyện tư duy logic và kỹ năng giải quyết vấn đề. Với nền tảng vững chắc này, bạn sẽ tự tin hơn trong việc tiếp cận các khía cạnh phức tạp hơn của vật lý và cơ học.