Chủ đề các dạng bài tập về momen lực: Các dạng bài tập về momen lực là chủ đề quan trọng trong chương trình học Vật Lý, giúp học sinh nắm vững khái niệm và ứng dụng thực tiễn. Bài viết này tổng hợp và phân loại các bài tập từ cơ bản đến nâng cao, cung cấp phương pháp giải chi tiết và ví dụ minh họa, giúp bạn tự tin chinh phục mọi thử thách trong môn học này.
Mục lục
Các Dạng Bài Tập Về Momen Lực
Momen lực là một khái niệm quan trọng trong vật lý, liên quan đến khả năng làm quay của một lực quanh một trục cố định. Dưới đây là tổng hợp các dạng bài tập phổ biến về momen lực, các công thức cơ bản, và phương pháp giải chi tiết.
I. Công Thức Tính Momen Lực
Momen lực được tính bằng công thức:
Trong đó:
- M: Momen lực
- F: Độ lớn của lực
- d: Cánh tay đòn, là khoảng cách từ trục quay đến điểm đặt lực
- θ: Góc giữa phương của lực và cánh tay đòn
Khi lực vuông góc với cánh tay đòn (θ = 90°), công thức trở nên đơn giản:
II. Các Dạng Bài Tập Về Momen Lực
Các dạng bài tập về momen lực thường xuất hiện trong các bài kiểm tra và đề thi. Dưới đây là một số dạng phổ biến:
-
Dạng 1: Momen Lực Của Một Lực Đơn Lẻ
Cho một lực F tác dụng tại một điểm trên vật, yêu cầu tính momen lực đối với một trục quay xác định.
-
Dạng 2: Momen Lực Trong Hệ Đòn Bẩy
Tính momen lực của các lực tác dụng lên đòn bẩy và xác định điều kiện để hệ đòn bẩy cân bằng.
-
Dạng 3: Momen Lực Trong Vật Rắn
Yêu cầu tính toán momen lực khi các lực tác dụng lên một vật rắn xung quanh nhiều trục khác nhau.
-
Dạng 4: Bài Tập Thực Tế Về Momen Lực
Ứng dụng momen lực trong các tình huống thực tế như trong máy móc, thiết bị cơ khí, hoặc trong xây dựng.
III. Ví Dụ Minh Họa
Dưới đây là một ví dụ minh họa cho bài tập về momen lực:
Bài tập: Một lực có độ lớn 10N tác dụng lên một vật với cánh tay đòn dài 2m và góc giữa lực và cánh tay đòn là 30°. Tính momen lực.
Giải:
IV. Lời Kết
Nắm vững công thức và phương pháp giải các bài tập về momen lực không chỉ giúp bạn đạt điểm cao trong các bài kiểm tra mà còn ứng dụng hiệu quả trong thực tế, đặc biệt trong các lĩnh vực kỹ thuật và cơ khí.

.png)
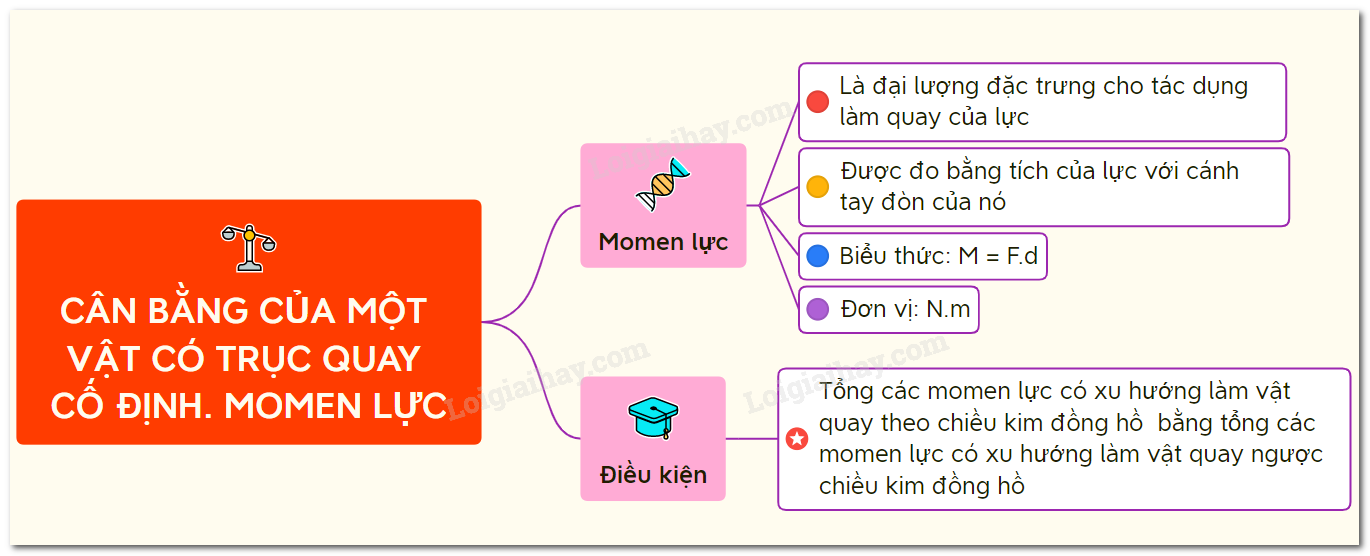
I. Giới Thiệu Về Momen Lực
Momen lực là một khái niệm cơ bản trong vật lý, đặc biệt quan trọng trong lĩnh vực cơ học. Nó đại diện cho khả năng làm quay của một lực khi tác dụng lên một vật quanh một trục cố định. Momen lực không chỉ giúp giải thích sự quay của các vật thể trong tự nhiên mà còn có ứng dụng rộng rãi trong nhiều ngành công nghiệp, như xây dựng, kỹ thuật và chế tạo máy móc.
Công thức tổng quát để tính momen lực được biểu diễn như sau:
Trong đó:
- M: Momen lực (đơn vị: Newton-mét, N·m)
- F: Lực tác dụng (đơn vị: Newton, N)
- d: Cánh tay đòn - khoảng cách từ trục quay đến điểm đặt lực (đơn vị: mét, m)
- θ: Góc giữa phương của lực và cánh tay đòn
Momen lực đạt giá trị lớn nhất khi lực tác dụng vuông góc với cánh tay đòn (θ = 90°), lúc này:
Khái niệm momen lực giúp chúng ta hiểu rõ hơn về cách các vật thể quay, cân bằng và chuyển động dưới tác dụng của các lực. Việc nắm vững kiến thức về momen lực là nền tảng quan trọng để học tốt các chủ đề khác trong vật lý và ứng dụng trong thực tiễn.
II. Công Thức Tính Momen Lực
Momen lực, hay còn gọi là momen xoắn, là một đại lượng vector đặc trưng cho sự quay của một vật thể dưới tác dụng của lực. Công thức tính momen lực được xây dựng dựa trên lực tác dụng và khoảng cách từ trục quay đến điểm đặt lực.
Công thức tổng quát để tính momen lực được biểu diễn như sau:
Trong đó:
- M: Momen lực (Newton-mét, N·m)
- F: Lực tác dụng (Newton, N)
- d: Cánh tay đòn - khoảng cách từ trục quay đến điểm đặt lực (mét, m)
- θ: Góc giữa lực và cánh tay đòn
Nếu lực tác dụng vuông góc với cánh tay đòn (θ = 90°), công thức sẽ đơn giản hơn:
Điều này có nghĩa là momen lực sẽ lớn nhất khi lực tác dụng vuông góc với cánh tay đòn. Ngược lại, nếu lực tác dụng song song với cánh tay đòn (θ = 0° hoặc θ = 180°), momen lực sẽ bằng không.
Momen lực được xác định bằng quy tắc bàn tay phải: nếu ngón cái chỉ theo chiều của lực, các ngón còn lại chỉ theo chiều quay của momen lực.
Công thức tính momen lực đóng vai trò quan trọng trong việc giải các bài toán cơ học, từ các bài tập đơn giản trong sách giáo khoa đến các ứng dụng phức tạp trong kỹ thuật và đời sống.

III. Các Dạng Bài Tập Về Momen Lực
Các dạng bài tập về momen lực thường được phân loại dựa trên cách áp dụng công thức tính momen lực và các tình huống thực tế trong cơ học. Dưới đây là các dạng bài tập phổ biến, giúp người học rèn luyện và củng cố kiến thức về momen lực.
-
Dạng 1: Tính Momen Lực Của Một Lực Đơn Lẻ
Dạng bài tập này yêu cầu tính toán momen lực khi chỉ có một lực tác dụng lên một vật quanh một trục cố định. Các bước thực hiện:
- Xác định điểm đặt lực và trục quay.
- Tính cánh tay đòn .
- Tính momen lực bằng công thức: .
-
Dạng 2: Tính Momen Lực Trong Hệ Đòn Bẩy
Đây là dạng bài tập áp dụng momen lực vào các hệ đòn bẩy, thường gặp trong thực tế. Các bước thực hiện:
- Xác định các lực tác dụng lên đòn bẩy.
- Tính momen lực của từng lực quanh trục quay.
- Xác định điều kiện cân bằng bằng cách so sánh tổng momen lực của các lực.
-
Dạng 3: Tính Momen Lực Trong Vật Rắn
Dạng bài tập này yêu cầu tính toán momen lực khi có nhiều lực tác dụng lên một vật rắn xung quanh nhiều trục quay. Các bước thực hiện:
- Xác định tất cả các lực tác dụng lên vật rắn.
- Tính momen lực của từng lực quanh mỗi trục quay.
- Tổng hợp momen lực để xác định kết quả cuối cùng.
-
Dạng 4: Bài Tập Thực Tế Về Momen Lực
Dạng bài tập này áp dụng momen lực vào các tình huống thực tế như trong các máy móc cơ khí, cầu trục, hoặc công trình xây dựng. Các bước thực hiện:
- Phân tích lực tác dụng và cánh tay đòn trong tình huống cụ thể.
- Áp dụng công thức tính momen lực để tìm kết quả.
- Đưa ra các giải pháp hoặc cải tiến dựa trên kết quả tính toán.
-
Dạng 5: Bài Tập Nâng Cao Về Momen Lực
Các bài tập nâng cao yêu cầu người học phải vận dụng nhiều kiến thức tổng hợp và kỹ năng tính toán momen lực trong các hệ phức tạp. Các bước thực hiện:
- Xác định tất cả các yếu tố ảnh hưởng đến momen lực.
- Phân tích và tính toán momen lực trong các tình huống đa lực, đa trục.
- Đưa ra kết luận và giải pháp dựa trên kết quả tính toán.
Việc luyện tập các dạng bài tập về momen lực giúp củng cố kiến thức lý thuyết và nâng cao khả năng ứng dụng thực tiễn, tạo nền tảng vững chắc cho các môn học liên quan đến cơ học và kỹ thuật.

IV. Phương Pháp Giải Các Bài Tập Momen Lực
Để giải các bài tập về momen lực một cách hiệu quả, người học cần nắm vững các phương pháp cơ bản và tuần tự áp dụng chúng theo từng bước. Dưới đây là các phương pháp giải phổ biến:
-
1. Phương Pháp Phân Tích Lực Tác Dụng
Phương pháp này đòi hỏi bạn phải xác định tất cả các lực tác dụng lên vật thể và hướng của từng lực. Các bước thực hiện:
- Xác định lực tác dụng chính, bao gồm trọng lực, lực kéo, lực ma sát, và các lực khác nếu có.
- Phân tích từng lực để xác định lực nào có ảnh hưởng đến momen lực quanh trục quay.
-
2. Phương Pháp Xác Định Trục Quay
Việc xác định đúng trục quay là yếu tố quan trọng trong quá trình giải bài tập momen lực. Các bước thực hiện:
- Xác định trục quay cố định của vật thể hoặc hệ thống đang xét.
- Đánh giá khoảng cách từ điểm đặt lực đến trục quay để tính cánh tay đòn.
- Áp dụng công thức momen lực: .
-
3. Phương Pháp Áp Dụng Điều Kiện Cân Bằng
Phương pháp này thường được sử dụng trong các bài toán yêu cầu tính toán momen lực trong hệ thống cân bằng. Các bước thực hiện:
- Đặt điều kiện tổng các momen lực quanh trục quay bằng không, tức là: .
- Giải hệ phương trình dựa trên điều kiện cân bằng để tìm giá trị của lực hoặc khoảng cách chưa biết.
- Kiểm tra lại kết quả để đảm bảo rằng hệ thống thực sự đang ở trạng thái cân bằng.
Khi nắm vững các phương pháp trên, việc giải các bài tập momen lực sẽ trở nên dễ dàng và chính xác hơn. Người học sẽ có thể áp dụng những kiến thức này vào các bài toán thực tiễn cũng như trong các tình huống thực tế khác.

V. Lời Kết
Qua bài viết này, chúng ta đã cùng nhau tìm hiểu về momen lực, từ khái niệm cơ bản, công thức tính toán cho đến các dạng bài tập và phương pháp giải. Momen lực là một trong những khái niệm quan trọng trong cơ học, không chỉ trong lý thuyết mà còn có nhiều ứng dụng thực tiễn trong đời sống và kỹ thuật.
Việc nắm vững momen lực sẽ giúp người học không chỉ giải quyết các bài toán cơ học mà còn hiểu sâu hơn về cách thức hoạt động của các hệ thống và máy móc trong thực tế. Hãy tiếp tục rèn luyện và áp dụng kiến thức này vào các tình huống cụ thể để trở thành một người học giỏi và thành công trong lĩnh vực này.
Cảm ơn bạn đã dành thời gian theo dõi bài viết. Chúc bạn học tập tốt và đạt được nhiều thành tựu trong quá trình học hỏi và khám phá thế giới cơ học đầy thú vị!