Chủ đề một ô tô đang chạy với vận tốc 72km/h: Một ô tô đang chạy với vận tốc 72km/h là một ví dụ điển hình để phân tích các khái niệm quan trọng trong vật lý về chuyển động thẳng biến đổi đều. Bài viết này sẽ giúp bạn hiểu rõ hơn về cách tính toán thời gian, quãng đường, và các ứng dụng thực tế trong việc phanh xe và đảm bảo an toàn giao thông.
Mục lục
Ô Tô Đang Chạy Với Vận Tốc 72km/h
Một ô tô đang di chuyển với vận tốc 72 km/h, khi tắt máy, xe sẽ chuyển động chậm dần đều. Để tính toán các thông số quan trọng trong quá trình này, ta cần xem xét gia tốc của xe, thời gian để xe dừng hẳn, và quãng đường mà xe di chuyển thêm.
1. Tính Thời Gian Để Xe Dừng Hẳn
Giả sử gia tốc chậm dần đều là \(a = 0.2 \, \text{m/s}^2\), ta có thể sử dụng công thức:
Với \(v_0 = 72 \, \text{km/h} = 20 \, \text{m/s}\), thời gian để xe dừng hẳn là:
2. Tính Quãng Đường Xe Chạy Thêm
Quãng đường xe chạy thêm từ lúc tắt máy đến khi dừng hẳn có thể tính bằng công thức:
Thay giá trị vào:
Như vậy, xe sẽ chạy thêm 1000m trước khi dừng lại hoàn toàn.
3. Vận Tốc Tức Thời
Phương trình vận tốc tức thời của xe có dạng:
Tại thời điểm \(t = 50 \, \text{giây}\), vận tốc của xe là:
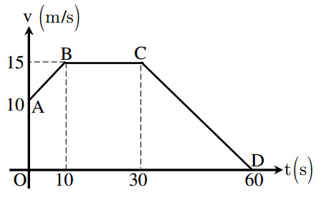
4. Đồ Thị Vận Tốc - Thời Gian
Đồ thị vận tốc - thời gian của xe trong quá trình này là một đường thẳng giảm dần, bắt đầu từ 20 m/s và giảm về 0 m/s sau 100 giây.
.png)
1. Tính Toán Về Chuyển Động Của Ô Tô
Khi một ô tô đang chạy với vận tốc 72km/h, ta có thể tiến hành các phép tính toán để xác định thời gian, quãng đường, và vận tốc tức thời trong quá trình xe giảm tốc độ hoặc dừng lại.
- Bước 1: Chuyển đổi đơn vị vận tốc từ km/h sang m/s:
- Bước 2: Tính thời gian để ô tô dừng lại:
- Bước 3: Tính quãng đường ô tô di chuyển thêm trước khi dừng hẳn:
- Bước 4: Tính vận tốc tức thời tại một thời điểm cụ thể:
- Bước 5: Tính gia tốc yêu cầu để dừng ô tô trong khoảng cách xác định:
Vận tốc ban đầu của ô tô là \(v_0 = 72 \, \text{km/h}\). Ta chuyển đổi sang đơn vị m/s:
\[ v_0 = \frac{72 \times 1000}{3600} = 20 \, \text{m/s} \]Giả sử ô tô chuyển động chậm dần đều với gia tốc \(a = 0.5 \, \text{m/s}^2\). Thời gian để ô tô dừng lại được tính bằng công thức:
\[ t = \frac{v_0}{a} = \frac{20}{0.5} = 40 \, \text{giây} \]Sử dụng công thức tính quãng đường trong chuyển động thẳng biến đổi đều:
\[ s = \frac{v_0^2}{2a} = \frac{20^2}{2 \times 0.5} = 400 \, \text{m} \]Ô tô sẽ di chuyển thêm 400m trước khi dừng hẳn.
Vận tốc tức thời \(v\) tại thời điểm \(t = 20 \, \text{giây}\) có thể được tính bằng:
\[ v = v_0 - at = 20 - 0.5 \times 20 = 10 \, \text{m/s} \]Giả sử ta muốn tính gia tốc cần thiết để dừng ô tô trong quãng đường \(s = 200 \, \text{m}\), sử dụng công thức:
\[ a = \frac{v_0^2}{2s} = \frac{20^2}{2 \times 200} = 1 \, \text{m/s}^2 \]Ô tô cần một gia tốc \(a = 1 \, \text{m/s}^2\) để dừng lại sau 200m.
2. Ứng Dụng Thực Tế Của Chuyển Động Thẳng Biến Đổi Đều
Chuyển động thẳng biến đổi đều là một hiện tượng vật lý thường gặp trong đời sống hàng ngày. Nó mô tả sự thay đổi vận tốc của một vật thể theo thời gian một cách đều đặn, thường là trong các trường hợp như phương tiện giao thông hoặc các vật thể bị ảnh hưởng bởi lực ma sát hoặc trọng lực.
Một ví dụ điển hình của chuyển động thẳng biến đổi đều là khi một ô tô đang chạy trên đường với vận tốc 72 km/h và bất ngờ gặp chướng ngại vật. Để đảm bảo an toàn, tài xế cần phải phanh gấp, làm cho xe chuyển động chậm dần đều.
- Khi ô tô hãm phanh, nó sẽ chuyển động chậm dần đều với gia tốc \[a = 5 \, m/s^2\].
- Quá trình này tuân theo phương trình vận tốc: \[v = v_0 + at\], trong đó \(v_0\) là vận tốc ban đầu và \(t\) là thời gian.
- Để tính khoảng cách tối thiểu cần thiết để ô tô dừng lại, ta có thể sử dụng công thức: \[S = v_0t + \frac{1}{2}at^2\].
Trong trường hợp thực tế, nếu ô tô đang chạy với vận tốc 72 km/h (tương đương 20 m/s) và hãm phanh với gia tốc \[a = -2.5 \, m/s^2\], ta có thể tính được thời gian cần để xe dừng lại hoàn toàn bằng cách giải phương trình:
Tiếp theo, quãng đường mà ô tô đi được từ lúc bắt đầu hãm phanh cho đến khi dừng lại có thể tính bằng:
Như vậy, trong tình huống này, ô tô cần một khoảng cách ít nhất là 80m để dừng lại an toàn trước khi va chạm với chướng ngại vật. Điều này minh chứng cho tầm quan trọng của việc nắm vững nguyên lý chuyển động thẳng biến đổi đều trong việc lái xe an toàn.

3. Phương Trình Vận Tốc Và Đồ Thị Vận Tốc - Thời Gian
Phương trình vận tốc là một trong những yếu tố quan trọng giúp mô tả chính xác sự thay đổi vận tốc của một vật thể theo thời gian. Khi một ô tô đang chạy với vận tốc 72 km/h, chúng ta có thể biểu diễn vận tốc của ô tô dưới dạng hàm số phụ thuộc vào thời gian.
Giả sử ô tô bắt đầu giảm tốc độ với gia tốc \(-a\), vận tốc của ô tô tại thời điểm \(t\) có thể được biểu diễn theo công thức:
Trong đó:
- \(v_0\) là vận tốc ban đầu (72 km/h, hay 20 m/s).
- \(a\) là gia tốc (có thể là âm nếu ô tô đang giảm tốc).
- \(t\) là thời gian.
Nếu ô tô đang giảm tốc với gia tốc \(-2 \, m/s^2\), phương trình vận tốc theo thời gian sẽ là:
Đồ thị vận tốc-thời gian biểu diễn mối quan hệ giữa vận tốc của ô tô và thời gian. Với gia tốc âm, đồ thị sẽ là một đường thẳng dốc xuống, bắt đầu từ điểm \(v_0\) trên trục tung và cắt trục hoành tại thời điểm \(t\) mà vận tốc bằng 0.
Đồ thị này không chỉ giúp chúng ta hình dung quá trình giảm tốc mà còn có thể được sử dụng để tính toán các đại lượng khác như quãng đường đi được và thời gian dừng lại của xe. Ví dụ, từ phương trình vận tốc ở trên, ta có thể xác định thời gian cần để xe dừng hẳn (khi \(v(t) = 0\)):
Đồ thị vận tốc-thời gian sẽ có dạng:
| Thời gian (s) | Vận tốc (m/s) |
| 0 | 20 |
| 5 | 10 |
| 10 | 0 |
Đồ thị này là một công cụ hữu ích để phân tích và hiểu rõ hơn về các quá trình động học trong thực tế, đặc biệt là trong các tình huống liên quan đến an toàn giao thông.

4. Bài Tập Thực Hành
Dưới đây là một số bài tập thực hành giúp bạn củng cố kiến thức về chuyển động thẳng đều và các khái niệm liên quan. Hãy giải từng bài tập để hiểu rõ hơn về cách tính toán vận tốc, quãng đường, và thời gian trong các tình huống thực tế.
-
Một ô tô đang chạy với vận tốc \(72 \, \text{km/h}\). Tính quãng đường mà ô tô đi được trong 10 phút.
Gợi ý: Sử dụng công thức tính quãng đường \(s = v \cdot t\) với \(v = 72 \, \text{km/h}\) và \(t = 10 \, \text{phút}\) (chuyển đổi thành giờ).
-
Một ô tô bắt đầu từ trạng thái nghỉ và đạt vận tốc \(72 \, \text{km/h}\) sau 20 giây. Tính gia tốc của ô tô.
Gợi ý: Sử dụng công thức \(v = at\) để tìm gia tốc \(a\).
-
Một ô tô đang chạy với vận tốc \(72 \, \text{km/h}\) thì bắt đầu giảm tốc đều với gia tốc \(2 \, \text{m/s}^2\). Tính thời gian để xe dừng hẳn và quãng đường mà xe đi được trong thời gian đó.
Gợi ý: Sử dụng phương trình vận tốc \(v(t) = v_0 + at\) và công thức quãng đường \(s = v_0t + \frac{1}{2}at^2\).
-
Vẽ đồ thị vận tốc-thời gian cho một ô tô đang chuyển động thẳng đều với vận tốc \(72 \, \text{km/h}\) trong 5 phút.
Gợi ý: Đồ thị sẽ là một đường thẳng song song với trục thời gian.
Các bài tập này giúp bạn không chỉ rèn luyện kỹ năng tính toán mà còn hiểu sâu hơn về các khái niệm vật lý cơ bản, đặc biệt là trong các tình huống thực tế liên quan đến chuyển động của ô tô.