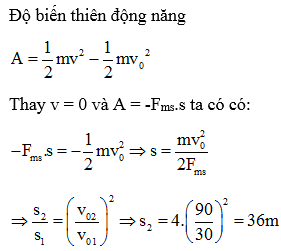Chủ đề khi đang chạy với vận tốc 36km/h: Khi đang chạy với vận tốc 36km/h, bạn không chỉ cần kiểm soát tốc độ mà còn phải chú ý đến an toàn trong quá trình di chuyển. Bài viết này sẽ hướng dẫn bạn cách duy trì vận tốc ổn định và ứng phó với các tình huống thực tế, từ việc phân tích chuyển động đến các kỹ năng lái xe an toàn.
Mục lục
- Thông tin tổng hợp về chủ đề "Khi đang chạy với vận tốc 36km/h"
- Mục lục tổng hợp nội dung
- 1. Khái niệm và lý thuyết cơ bản về vận tốc
- 2. Bài toán vận tốc trong chuyển động thẳng
- 3. Phân tích chuyển động khi xe xuống dốc với vận tốc 36km/h
- 4. Ứng dụng thực tế của kiến thức về vận tốc
- 5. Các bài tập vận dụng nâng cao
Thông tin tổng hợp về chủ đề "Khi đang chạy với vận tốc 36km/h"
Chủ đề này thường được đề cập trong các bài tập vật lý liên quan đến chuyển động thẳng biến đổi đều. Dưới đây là tổng hợp chi tiết về những thông tin phổ biến xoay quanh từ khóa này:
1. Bài toán vật lý liên quan đến chuyển động thẳng
-
Khi một ô tô đang chạy với vận tốc 36 km/h, nhiều bài tập thường đặt vấn đề tính toán các đại lượng như quãng đường, thời gian, gia tốc hoặc vận tốc cuối cùng khi ô tô chuyển động trên một đoạn đường, đặc biệt là khi xuống dốc.
-
Một ví dụ điển hình là việc ô tô bắt đầu chạy xuống dốc với vận tốc ban đầu 36 km/h và có gia tốc nhất định. Công thức tính toán phổ biến được sử dụng:
\[ s = v_0 \cdot t + \frac{1}{2} a t^2 \]
\[ v = v_0 + a \cdot t \]
2. Ứng dụng trong đời sống
-
Những bài toán này không chỉ có ý nghĩa trong việc luyện tập kiến thức vật lý mà còn áp dụng thực tiễn trong việc hiểu về chuyển động của phương tiện giao thông, giúp người học có cái nhìn rõ ràng hơn về cách thức hoạt động của các phương tiện khi tham gia giao thông trên đường.
-
Ví dụ, việc hiểu rõ cách tính vận tốc và gia tốc có thể giúp các kỹ sư thiết kế các hệ thống phanh an toàn cho xe cộ khi di chuyển trên những địa hình dốc hoặc khi xe mất phanh.
3. Câu hỏi thường gặp trong các bài thi
-
Đề tài "khi đang chạy với vận tốc 36km/h" thường xuất hiện trong các đề kiểm tra vật lý ở bậc trung học phổ thông. Học sinh cần nắm vững các công thức liên quan và biết cách áp dụng chúng vào thực tế.
-
Một số bài tập yêu cầu học sinh tính toán thời điểm hai xe gặp nhau, quãng đường đi được hoặc xác định vị trí của xe tại một thời điểm nhất định.
4. Các yếu tố cần lưu ý
Khi giải các bài toán này, cần chú ý đến đơn vị của các đại lượng vật lý (ví dụ: chuyển đổi km/h sang m/s) để đảm bảo tính toán chính xác. Việc hiểu rõ bản chất vật lý của vấn đề cũng giúp tránh sai sót trong quá trình giải bài tập.
| Chủ đề | Chi tiết |
| Vận tốc ban đầu | 36 km/h (10 m/s) |
| Gia tốc | Thường là gia tốc không đổi trong các bài tập |
| Quãng đường | 960 m (ví dụ trong bài toán cụ thể) |
| Thời gian | Tính toán dựa trên các công thức vật lý liên quan |
Tóm lại, chủ đề "khi đang chạy với vận tốc 36km/h" là một phần quan trọng trong chương trình vật lý, giúp người học áp dụng kiến thức vào các tình huống thực tế và cải thiện khả năng tính toán, phân tích vấn đề.

1. Khái niệm và lý thuyết cơ bản về vận tốc
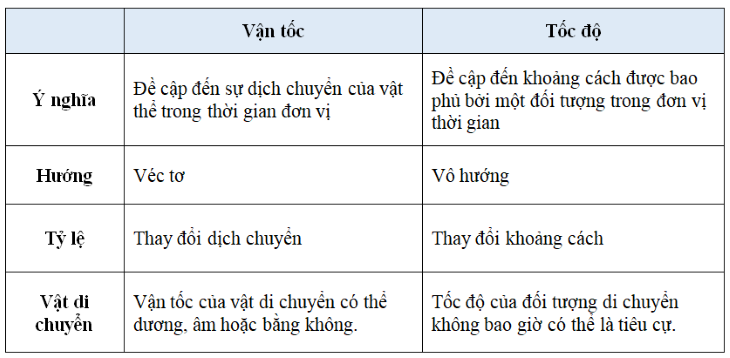
Vận tốc là đại lượng vật lý cơ bản, thể hiện sự thay đổi vị trí của vật thể theo thời gian trong không gian. Đơn vị đo vận tốc phổ biến là mét trên giây (m/s) hoặc kilômét trên giờ (km/h).
Vận tốc được xác định bằng công thức:
Trong đó:
- v là vận tốc,
- s là quãng đường,
- t là thời gian.
Vận tốc có thể là đại lượng vô hướng (khi chỉ xét độ lớn) hoặc đại lượng vector (khi xét cả độ lớn và hướng). Trong chuyển động thẳng đều, vận tốc không đổi; trong chuyển động thẳng biến đổi đều, vận tốc thay đổi tuyến tính theo thời gian.

2. Bài toán vận tốc trong chuyển động thẳng
Bài toán vận tốc trong chuyển động thẳng là một trong những bài toán cơ bản trong cơ học, giúp chúng ta hiểu rõ hơn về cách một vật di chuyển trong không gian và thời gian. Dưới đây là một số bài toán thường gặp:
2.1. Tính toán thời gian và quãng đường khi biết vận tốc
Khi biết vận tốc và một trong hai yếu tố thời gian hoặc quãng đường, chúng ta có thể dễ dàng tính toán yếu tố còn lại bằng cách sử dụng các công thức cơ bản:
Ví dụ, khi một xe đang chạy với vận tốc 36 km/h, nếu biết thời gian hoặc quãng đường, chúng ta có thể tính toán các yếu tố còn lại.
2.2. Các bài tập về chuyển động thẳng biến đổi đều
Chuyển động thẳng biến đổi đều là loại chuyển động trong đó vận tốc thay đổi đều theo thời gian. Công thức tính vận tốc tại thời điểm bất kỳ có thể được mô tả như sau:
Trong đó:
- v là vận tốc tại thời điểm t,
- v_0 là vận tốc ban đầu,
- a là gia tốc,
- t là thời gian.
Ví dụ, khi xe bắt đầu tăng tốc từ vận tốc 36 km/h với gia tốc \(a = 2\) m/s², chúng ta có thể tính toán vận tốc tại thời điểm bất kỳ.
2.3. Ứng dụng công thức trong bài toán thực tế
Trong thực tế, bài toán vận tốc thường liên quan đến nhiều yếu tố khác như lực cản, độ dốc, hoặc sự thay đổi vận tốc. Một ví dụ điển hình là khi xe đang chạy với vận tốc 36 km/h, việc tính toán lực cản gió hoặc ảnh hưởng của địa hình sẽ giúp dự đoán chính xác hơn về quãng đường và thời gian cần thiết.

3. Phân tích chuyển động khi xe xuống dốc với vận tốc 36km/h
Khi xe đang xuống dốc với vận tốc 36km/h, các yếu tố như độ dốc của đường, lực cản không khí và trọng lực sẽ ảnh hưởng đáng kể đến chuyển động của xe. Để phân tích chính xác, chúng ta cần xem xét các yếu tố này một cách chi tiết:
3.1. Tính toán vận tốc cuối cùng khi xuống dốc
Giả sử xe bắt đầu xuống dốc từ vận tốc 36km/h, chúng ta có thể tính toán vận tốc cuối cùng tại chân dốc bằng công thức:
Trong đó:
- v_f là vận tốc cuối cùng,
- v_0 là vận tốc ban đầu (36km/h),
- g là gia tốc trọng trường,
- h là chiều cao của dốc.
Phương trình trên cho thấy, khi xe xuống dốc, vận tốc sẽ tăng lên do tác động của lực hấp dẫn.
3.2. Ảnh hưởng của gia tốc trong chuyển động thẳng nhanh dần đều
Trong quá trình xuống dốc, xe sẽ chịu tác động của gia tốc trọng trường, khiến vận tốc tăng dần đều theo thời gian. Gia tốc này được tính toán theo công thức:
Trong đó:
- a là gia tốc của xe khi xuống dốc,
- g là gia tốc trọng trường,
- \theta là góc nghiêng của dốc.
Gia tốc này làm cho xe nhanh dần đều, nghĩa là vận tốc xe sẽ tăng tuyến tính theo thời gian, nếu bỏ qua lực cản.
3.3. Phân tích các bài toán điển hình
Khi phân tích chuyển động của xe khi xuống dốc, ta cần chú ý đến các bài toán điển hình như:
- Bài toán tính thời gian để xe xuống hết dốc.
- Bài toán xác định quãng đường xe di chuyển khi xuống dốc.
- Bài toán tính lực cản không khí và ảnh hưởng của nó đến vận tốc cuối cùng của xe.
Việc hiểu rõ các yếu tố này giúp dự đoán và điều chỉnh chuyển động của xe trong thực tế, đảm bảo an toàn khi lái xe trên các đoạn đường dốc.

4. Ứng dụng thực tế của kiến thức về vận tốc
Kiến thức về vận tốc không chỉ đóng vai trò quan trọng trong lý thuyết mà còn mang lại nhiều ứng dụng thực tế trong cuộc sống hàng ngày. Việc hiểu rõ về vận tốc giúp tối ưu hóa an toàn giao thông, thiết kế hệ thống đường sá và đánh giá hiệu quả hoạt động của phương tiện giao thông.
- Thiết kế và an toàn giao thông:
Kiến thức về vận tốc giúp các kỹ sư thiết kế đường bộ và hệ thống giao thông công cộng, đảm bảo rằng các phương tiện di chuyển an toàn và hiệu quả. Ví dụ, việc tính toán chính xác vận tốc tối đa cho phép trên các đoạn đường khác nhau dựa trên điều kiện địa hình và thời tiết là cực kỳ quan trọng.
- Đánh giá hiệu quả phanh xe:
Hiểu rõ về vận tốc giúp phân tích quá trình giảm tốc và hiệu quả của hệ thống phanh trong các phương tiện giao thông. Điều này có thể cứu sống nhiều người bằng cách cải tiến công nghệ phanh và giảm nguy cơ tai nạn giao thông.
- Tầm quan trọng của vận tốc trong các tình huống giao thông:
Việc điều chỉnh vận tốc hợp lý trong các tình huống giao thông khác nhau giúp tránh được các sự cố đáng tiếc. Ví dụ, việc giảm tốc độ khi đến gần ngã tư hoặc khi tham gia vào giao thông đông đúc có thể giảm thiểu rủi ro tai nạn.
XEM THÊM:
5. Các bài tập vận dụng nâng cao
Các bài tập vận dụng nâng cao giúp củng cố kiến thức về vận tốc và khả năng áp dụng vào thực tế. Dưới đây là một số bài toán tiêu biểu:
5.1. Bài toán kết hợp nhiều đại lượng vật lý
Bài toán này yêu cầu tính toán vận tốc khi biết các đại lượng khác như gia tốc, thời gian, và quãng đường. Ví dụ:
Trong đó:
- v_0: Vận tốc ban đầu (có thể là 36 km/h),
- a: Gia tốc,
- t: Thời gian.
Giả sử, xe đang di chuyển với vận tốc 36 km/h, và bắt đầu tăng tốc với gia tốc \( a = 2 \, m/s^2 \) trong thời gian 5 giây, hãy tính vận tốc cuối cùng.
5.2. Tính toán khi có thêm yếu tố lực cản
Bài toán này đòi hỏi tính toán vận tốc của xe khi chịu thêm lực cản từ môi trường. Công thức có thể phức tạp hơn khi cần xét đến lực cản không khí, ma sát, v.v.:
Trong đó, k là hệ số cản. Bài toán yêu cầu tính toán vận tốc cuối cùng khi xe di chuyển với vận tốc 36 km/h trên một đoạn đường với lực cản không khí.
5.3. Bài tập tổng hợp nâng cao
Bài tập tổng hợp nâng cao có thể yêu cầu kết hợp các công thức và hiểu biết về vận tốc, gia tốc, lực, và thời gian để giải quyết các tình huống thực tế phức tạp. Ví dụ, tính toán quãng đường xe sẽ đi được trước khi dừng hẳn khi biết vận tốc ban đầu, hệ số ma sát và thời gian phanh:
Trong đó:
- v_0: Vận tốc ban đầu (36 km/h),
- \mu: Hệ số ma sát giữa lốp xe và mặt đường,
- g: Gia tốc trọng trường.
Bài toán này yêu cầu hiểu biết sâu về các khái niệm vật lý và kỹ năng tính toán chính xác để có thể giải quyết hiệu quả.

.png)