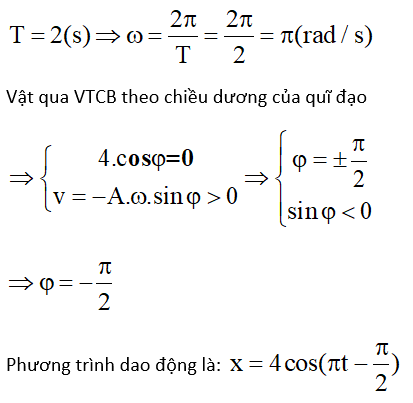Chủ đề phương trình vận tốc lớp 12: Phương trình vận tốc lớp 12 là một trong những chủ đề quan trọng trong môn Vật lý, giúp học sinh nắm vững kiến thức về chuyển động. Bài viết này sẽ cung cấp hướng dẫn chi tiết cùng các ứng dụng thực tế, giúp bạn hiểu sâu hơn và áp dụng hiệu quả trong các bài toán liên quan.
Mục lục
Phương Trình Vận Tốc Lớp 12
Phương trình vận tốc là một trong những khái niệm quan trọng trong chương trình Vật lý lớp 12. Nó giúp học sinh hiểu rõ hơn về các hiện tượng vật lý liên quan đến chuyển động, đặc biệt là trong các bài toán về dao động, chuyển động thẳng và các hiện tượng liên quan đến vận tốc.
1. Các Khái Niệm Cơ Bản
- Vận tốc: Là đại lượng vectơ biểu thị mức độ nhanh hay chậm của sự thay đổi vị trí của vật theo thời gian.
- Phương trình vận tốc: Được thiết lập dựa trên sự liên hệ giữa vận tốc, thời gian và các đại lượng khác như gia tốc và vị trí.
2. Công Thức Phương Trình Vận Tốc
Phương trình vận tốc có thể được biểu diễn qua các dạng khác nhau, tùy thuộc vào bài toán và các điều kiện ban đầu. Một số công thức phổ biến bao gồm:
- Phương trình chuyển động thẳng đều:
- Phương trình chuyển động thẳng biến đổi đều:
- Vận tốc trong dao động điều hòa:
\[ v = \frac{\Delta s}{\Delta t} \]
\[ v = v_0 + at \]
\[ v = -\omega A \sin(\omega t + \varphi) \]
3. Ứng Dụng Thực Tế
Phương trình vận tốc không chỉ là một công cụ toán học mà còn có ứng dụng rộng rãi trong cuộc sống. Một số ứng dụng bao gồm:
- Giải bài toán chuyển động: Tính toán thời gian, vận tốc và quãng đường di chuyển của các đối tượng trong các tình huống thực tế như xe cộ, máy bay.
- Ứng dụng trong kỹ thuật: Sử dụng để thiết kế và điều chỉnh các hệ thống chuyển động trong cơ khí, robot và các thiết bị tự động hóa.
4. Một Số Bài Tập Mẫu
Dưới đây là một số bài tập mẫu liên quan đến phương trình vận tốc mà học sinh lớp 12 thường gặp:
- Bài toán dao động điều hòa: Một vật dao động điều hòa với phương trình \( x = 5\cos(2\pi t + \frac{\pi}{3}) \). Hãy tính vận tốc của vật tại thời điểm \( t = 1 \) giây.
- Bài toán chuyển động thẳng: Một xe máy di chuyển từ điểm A đến điểm B với vận tốc ban đầu là \( 20 \, \text{km/h} \) và gia tốc không đổi là \( 2 \, \text{m/s}^2 \). Hãy xác định vận tốc của xe sau 10 giây.
5. Lưu Ý Khi Giải Bài Tập
- Xác định đúng công thức: Đảm bảo rằng công thức sử dụng là phù hợp với điều kiện bài toán.
- Kiểm tra đơn vị: Luôn kiểm tra và chuyển đổi đơn vị nếu cần thiết để tránh sai sót trong tính toán.
.png)
1. Giới thiệu về phương trình vận tốc
Phương trình vận tốc là một trong những kiến thức quan trọng trong chương trình Vật lý lớp 12, giúp học sinh hiểu rõ hơn về mối quan hệ giữa quãng đường, thời gian và vận tốc trong các hiện tượng chuyển động. Phương trình vận tốc được sử dụng để mô tả chuyển động của các vật thể trong các điều kiện khác nhau, từ chuyển động thẳng đều đến chuyển động thẳng biến đổi đều và dao động điều hòa.
Trong chương trình Vật lý lớp 12, học sinh sẽ được tiếp cận với nhiều loại phương trình vận tốc, bao gồm:
- Phương trình chuyển động thẳng đều: Mô tả vận tốc không đổi của một vật khi không có lực tác động.
- Phương trình chuyển động thẳng biến đổi đều: Mô tả sự thay đổi vận tốc theo thời gian dưới tác động của một lực không đổi.
- Phương trình vận tốc trong dao động điều hòa: Mô tả vận tốc của một vật dao động với biên độ và tần số không đổi.
Việc nắm vững các phương trình vận tốc sẽ giúp học sinh không chỉ giải quyết các bài toán lý thuyết mà còn ứng dụng vào các tình huống thực tế, từ đó phát triển tư duy logic và kỹ năng phân tích vấn đề một cách hiệu quả.
2. Các loại phương trình vận tốc
Trong Vật lý lớp 12, có nhiều loại phương trình vận tốc được sử dụng để mô tả các kiểu chuyển động khác nhau. Dưới đây là ba loại phương trình vận tốc phổ biến nhất mà học sinh cần nắm vững:
- Phương trình chuyển động thẳng đều:
Chuyển động thẳng đều là chuyển động mà vận tốc của vật không đổi theo thời gian, tức là vật di chuyển một quãng đường bằng nhau trong những khoảng thời gian bằng nhau. Phương trình của chuyển động thẳng đều có dạng:
\[ v = \frac{s}{t} \]
Trong đó:
- \(v\): vận tốc (m/s)
- \(s\): quãng đường đi được (m)
- \(t\): thời gian (s)
- Phương trình chuyển động thẳng biến đổi đều:
Chuyển động thẳng biến đổi đều là chuyển động mà vận tốc của vật thay đổi đều đặn theo thời gian do tác động của gia tốc. Phương trình của chuyển động thẳng biến đổi đều có dạng:
\[ v = v_0 + at \]
Trong đó:
- \(v_0\): vận tốc ban đầu (m/s)
- \(a\): gia tốc (m/s2)
- \(t\): thời gian (s)
Đối với quãng đường đi được, phương trình có dạng:
\[ s = v_0t + \frac{1}{2}at^2 \]
- Phương trình vận tốc trong dao động điều hòa:
Trong dao động điều hòa, vận tốc của vật thay đổi theo một hàm số sin hoặc cosin theo thời gian. Phương trình vận tốc của dao động điều hòa có dạng:
\[ v = -\omega A \sin(\omega t + \varphi) \]
Trong đó:
- \(\omega\): tần số góc (rad/s)
- \(A\): biên độ dao động (m)
- \(\varphi\): pha ban đầu (rad)
Việc nắm vững các loại phương trình vận tốc trên sẽ giúp học sinh giải quyết hiệu quả các bài toán về chuyển động trong Vật lý lớp 12, từ đó phát triển tư duy khoa học và khả năng phân tích các hiện tượng tự nhiên.

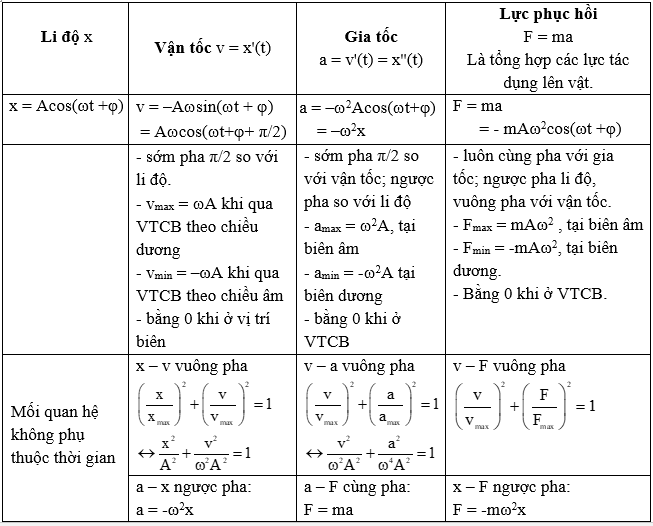
3. Các công thức liên quan đến phương trình vận tốc
Phương trình vận tốc là nền tảng quan trọng trong Vật lý lớp 12, và có nhiều công thức liên quan mà học sinh cần nắm vững để giải quyết các bài toán về chuyển động. Dưới đây là các công thức chính thường được sử dụng:
- Công thức tính vận tốc trung bình:
- Công thức tính vận tốc tức thời:
- Công thức liên hệ giữa vận tốc, gia tốc và thời gian:
- Công thức liên hệ giữa vận tốc, quãng đường và gia tốc:
- Công thức vận tốc trong dao động điều hòa:
Vận tốc trung bình của một vật trong khoảng thời gian \( t \) khi di chuyển quãng đường \( s \) được tính theo công thức:
\[ v_{tb} = \frac{s}{t} \]
Vận tốc tức thời là vận tốc của vật tại một thời điểm cụ thể, được xác định bằng đạo hàm của vị trí theo thời gian:
\[ v(t) = \frac{ds}{dt} \]
Công thức này mô tả mối liên hệ giữa vận tốc ban đầu, gia tốc và thời gian trong chuyển động thẳng biến đổi đều:
\[ v = v_0 + at \]
Công thức này giúp xác định vận tốc của vật khi biết quãng đường đã di chuyển và gia tốc:
\[ v^2 = v_0^2 + 2as \]
Trong dao động điều hòa, vận tốc của vật tại thời điểm \( t \) được xác định như sau:
\[ v = -\omega A \sin(\omega t + \varphi) \]
Hiểu và áp dụng đúng các công thức này sẽ giúp học sinh giải quyết hiệu quả các bài toán về vận tốc trong chương trình Vật lý lớp 12, từ những bài toán đơn giản đến những bài toán phức tạp hơn liên quan đến dao động và chuyển động thẳng.

4. Ứng dụng của phương trình vận tốc trong các bài toán
Phương trình vận tốc không chỉ là lý thuyết mà còn có nhiều ứng dụng quan trọng trong các bài toán Vật lý, giúp học sinh hiểu rõ hơn về bản chất của chuyển động và các hiện tượng liên quan. Dưới đây là một số ứng dụng cụ thể của phương trình vận tốc trong các bài toán:
- Ứng dụng trong bài toán chuyển động thẳng đều:
Trong các bài toán về chuyển động thẳng đều, phương trình vận tốc được sử dụng để xác định quãng đường mà một vật di chuyển trong một khoảng thời gian nhất định khi biết vận tốc của nó. Ví dụ, khi biết vận tốc \(v\) và thời gian \(t\), quãng đường \(s\) có thể được tính bằng công thức:
\[ s = v \times t \]
- Ứng dụng trong bài toán chuyển động thẳng biến đổi đều:
Phương trình vận tốc trong chuyển động thẳng biến đổi đều giúp tính toán vận tốc của vật sau một khoảng thời gian khi biết vận tốc ban đầu và gia tốc. Ví dụ, khi một vật bắt đầu chuyển động với vận tốc ban đầu \(v_0\) và chịu tác dụng của gia tốc \(a\), vận tốc sau thời gian \(t\) được tính bằng:
\[ v = v_0 + at \]
Phương trình này còn được sử dụng để xác định quãng đường di chuyển của vật trong thời gian \(t\) bằng công thức:
\[ s = v_0t + \frac{1}{2}at^2 \]
- Ứng dụng trong bài toán dao động điều hòa:
Trong dao động điều hòa, phương trình vận tốc giúp xác định vận tốc của vật tại một thời điểm cụ thể. Khi biết biên độ \(A\), tần số góc \(\omega\) và pha ban đầu \(\varphi\), vận tốc của vật tại thời điểm \(t\) được tính bằng:
\[ v = -\omega A \sin(\omega t + \varphi) \]
Bài toán dao động điều hòa thường yêu cầu xác định vận tốc lớn nhất và vận tốc tại các vị trí đặc biệt trong chu kỳ dao động.
- Ứng dụng trong bài toán thực tế:
Phương trình vận tốc còn được áp dụng trong các bài toán thực tế như tính toán quãng đường và thời gian di chuyển của xe cộ, máy bay, và các phương tiện giao thông khác. Ví dụ, để xác định thời gian cần thiết để một chiếc xe di chuyển một quãng đường \(s\) với vận tốc trung bình \(v\), ta sử dụng công thức:
\[ t = \frac{s}{v} \]
Việc ứng dụng linh hoạt các phương trình vận tốc trong các bài toán không chỉ giúp học sinh giải quyết các bài tập trên lớp mà còn hiểu rõ hơn về các hiện tượng trong cuộc sống hàng ngày, từ đó phát triển khả năng tư duy logic và kỹ năng giải quyết vấn đề.

5. Lưu ý khi giải bài tập về phương trình vận tốc
Khi giải bài tập về phương trình vận tốc trong chương trình Vật lý lớp 12, học sinh cần lưu ý một số điểm quan trọng để tránh những sai lầm phổ biến và đạt được kết quả chính xác. Dưới đây là các lưu ý chi tiết:
- Xác định đúng loại chuyển động:
Trước khi giải bài toán, cần xác định rõ loại chuyển động của vật là chuyển động thẳng đều, thẳng biến đổi đều, hay dao động điều hòa. Điều này giúp lựa chọn đúng phương trình vận tốc và các công thức liên quan.
- Chú ý đến đơn vị đo:
Khi giải các bài toán liên quan đến vận tốc, cần đảm bảo rằng các đơn vị đo như mét (m), giây (s), và mét trên giây (m/s) phải nhất quán. Việc không chú ý đến đơn vị có thể dẫn đến kết quả sai lầm.
- Kiểm tra dấu của đại lượng:
Trong các bài toán có gia tốc, dấu của gia tốc (\(a\)) cần được xác định chính xác. Gia tốc dương hoặc âm tùy thuộc vào việc vật đang tăng tốc hay giảm tốc.
- Sử dụng đúng công thức:
Đối với mỗi loại bài toán, chỉ sử dụng công thức phù hợp. Ví dụ, đối với chuyển động thẳng đều, chỉ cần sử dụng công thức đơn giản \(v = \frac{s}{t}\), trong khi với chuyển động thẳng biến đổi đều, cần sử dụng các công thức phức tạp hơn như \(v = v_0 + at\) hoặc \(v^2 = v_0^2 + 2as\).
- Vẽ sơ đồ hoặc biểu đồ:
Trong nhiều trường hợp, việc vẽ sơ đồ hoặc biểu đồ chuyển động sẽ giúp bạn hình dung rõ ràng hơn về quá trình chuyển động của vật, từ đó dễ dàng áp dụng các phương trình vận tốc để giải bài toán.
- Kiểm tra lại kết quả:
Sau khi giải xong, hãy kiểm tra lại kết quả bằng cách thay ngược lại các giá trị đã tìm được vào phương trình gốc để đảm bảo tính chính xác.
Những lưu ý trên sẽ giúp học sinh không chỉ giải quyết bài tập về phương trình vận tốc một cách hiệu quả mà còn nâng cao kỹ năng phân tích và xử lý các vấn đề phức tạp trong Vật lý.
XEM THÊM:
6. Tổng kết và các bài tập mẫu
Qua các phần đã học, chúng ta đã nắm vững các khái niệm, công thức và phương pháp giải quyết bài toán liên quan đến phương trình vận tốc trong chương trình Vật lý lớp 12. Dưới đây là tổng kết những điểm quan trọng cần ghi nhớ và một số bài tập mẫu giúp củng cố kiến thức.
- Tổng kết:
- Phương trình vận tốc là một công cụ quan trọng để mô tả chuyển động của vật trong các loại chuyển động khác nhau như chuyển động thẳng đều, chuyển động thẳng biến đổi đều, và dao động điều hòa.
- Các công thức quan trọng bao gồm: công thức tính vận tốc trung bình, vận tốc tức thời, và các công thức liên hệ giữa vận tốc, gia tốc, quãng đường, và thời gian.
- Việc nắm vững cách áp dụng các công thức này vào bài toán thực tế là yếu tố quan trọng để đạt được kết quả chính xác.
- Cần chú ý đến các đơn vị đo lường, dấu của các đại lượng và kiểm tra lại kết quả sau khi giải xong bài toán.
- Bài tập mẫu:
- Bài tập 1: Một vật di chuyển với vận tốc ban đầu \(v_0 = 5 \, \text{m/s}\) và gia tốc \(a = 2 \, \text{m/s}^2\). Tính vận tốc của vật sau \(t = 10 \, \text{s}\) và quãng đường mà vật đã đi được trong thời gian đó.
- Bài tập 2: Một xe ô tô di chuyển từ A đến B với vận tốc trung bình \(v_{tb} = 60 \, \text{km/h}\). Tính thời gian cần thiết để xe di chuyển quãng đường \(s = 120 \, \text{km}\).
- Bài tập 3: Một vật dao động điều hòa với biên độ \(A = 10 \, \text{cm}\), tần số góc \(\omega = 2 \, \text{rad/s}\). Tính vận tốc của vật tại thời điểm \(t = 5 \, \text{s}\) và vận tốc cực đại của vật.
Thông qua các bài tập trên, học sinh sẽ có cơ hội ôn tập và củng cố kiến thức, đồng thời rèn luyện kỹ năng giải quyết bài toán liên quan đến phương trình vận tốc một cách hiệu quả.