Chủ đề đạo hàm vận tốc: Đạo hàm vận tốc không chỉ là một khái niệm toán học quan trọng mà còn là nền tảng trong việc phân tích chuyển động và ứng dụng thực tiễn trong vật lý và kỹ thuật. Bài viết này sẽ giúp bạn hiểu rõ về đạo hàm vận tốc, từ các công thức cơ bản đến các ứng dụng thực tế hàng ngày.
Mục lục
Đạo Hàm Vận Tốc: Khái Niệm, Công Thức và Ứng Dụng
Đạo hàm vận tốc là một khái niệm cơ bản trong toán học và vật lý, được sử dụng để mô tả sự thay đổi của vận tốc theo thời gian. Khái niệm này có vai trò quan trọng trong việc phân tích và mô tả chuyển động của các vật thể.
Khái Niệm Đạo Hàm Vận Tốc
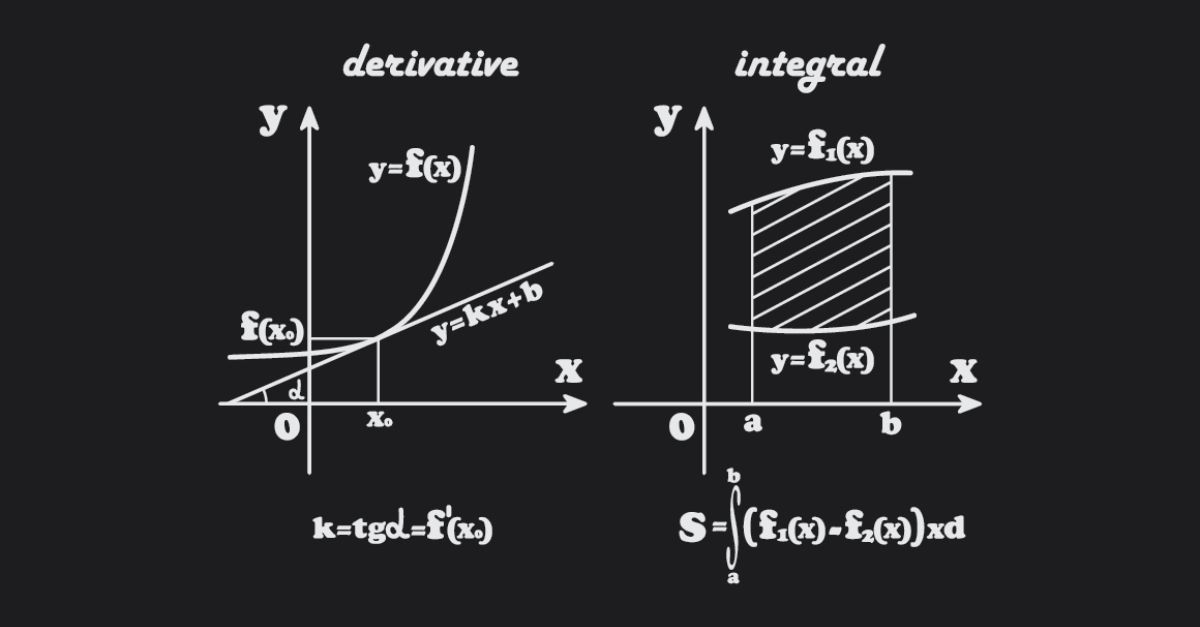
Vận tốc của một vật thể tại một thời điểm cụ thể được xác định bằng đạo hàm của hàm vị trí \(s(t)\) theo thời gian \(t\). Công thức toán học của đạo hàm vận tốc được biểu diễn như sau:
\[
v(t) = \frac{ds(t)}{dt}
\]
Trong đó:
- \(v(t)\) là vận tốc tức thời của vật thể tại thời điểm \(t\).
- \(s(t)\) là hàm vị trí của vật thể theo thời gian.
- \(\frac{ds(t)}{dt}\) là đạo hàm của \(s(t)\) theo \(t\).
Công Thức Đạo Hàm Vận Tốc
Các công thức đạo hàm vận tốc phổ biến trong các bài toán vật lý bao gồm:
- Nếu \(s(t)\) là một đa thức bậc hai: \(s(t) = at^2 + bt + c\), thì \(v(t)\) được tính bằng:
- Nếu \(s(t)\) là một hàm bậc ba: \(s(t) = at^3 + bt^2 + ct + d\), thì:
- Nếu \(s(t)\) là một hàm mũ: \(s(t) = ae^{bt}\), thì:
\[
v(t) = 2at + b
\]
\[
v(t) = 3at^2 + 2bt + c
\]
\[
v(t) = abe^{bt}
\]
Ví Dụ Minh Họa Đạo Hàm Vận Tốc
Để hiểu rõ hơn về cách tính đạo hàm vận tốc, hãy xem xét ví dụ sau:
Giả sử một vật thể chuyển động theo phương trình vị trí:
\[
s(t) = t^2 - 5t + 6
\]
Để tìm vận tốc tức thời \(v(t)\) tại thời điểm bất kỳ, ta tính đạo hàm của \(s(t)\) theo \(t\):
\[
v(t) = 2t - 5
\]
Vận tốc tức thời tại \(t = 3\) giây là:
\[
v(3) = 2(3) - 5 = 1 \text{ m/s}
\]
Ứng Dụng Của Đạo Hàm Vận Tốc
Đạo hàm vận tốc được áp dụng rộng rãi trong nhiều lĩnh vực của vật lý, bao gồm:
- Phân tích chuyển động: Giúp xác định vận tốc và gia tốc tức thời của vật thể trong các bài toán chuyển động.
- Chuyển động rơi tự do: Sử dụng để tính vận tốc và gia tốc của vật thể rơi trong trường trọng lực.
- Kỹ thuật cơ học: Đạo hàm vận tốc hỗ trợ trong thiết kế và phân tích các hệ thống cơ học phức tạp.
Bảng Tóm Tắt Các Công Thức Đạo Hàm Vận Tốc
| Hàm vị trí \(s(t)\) | Vận tốc \(v(t)\) | Gia tốc \(a(t)\) |
|---|---|---|
| \(at^2 + bt + c\) | \(2at + b\) | \(2a\) |
| \(at^3 + bt^2 + ct + d\) | \(3at^2 + 2bt + c\) | \(6at + 2b\) |
| \(ae^{bt}\) | \(abe^{bt}\) | \(ab^2e^{bt}\) |
Như vậy, đạo hàm vận tốc là một công cụ mạnh mẽ để phân tích và dự đoán chuyển động của các vật thể, đồng thời có nhiều ứng dụng thực tế trong khoa học và kỹ thuật.

.png)
1. Giới thiệu về Đạo Hàm Vận Tốc
Đạo hàm vận tốc là một khái niệm quan trọng trong toán học và vật lý, được sử dụng để mô tả sự thay đổi của vị trí theo thời gian. Nó đóng vai trò cốt lõi trong việc phân tích chuyển động và xác định các đại lượng vật lý như vận tốc và gia tốc.
Trong toán học, vận tốc được định nghĩa là đạo hàm của vị trí theo thời gian. Nếu hàm vị trí của một vật thể được biểu diễn bằng \(s(t)\), thì vận tốc tức thời của vật thể đó tại thời điểm \(t\) được tính bằng đạo hàm của \(s(t)\) theo \(t\):
\[
v(t) = \frac{ds(t)}{dt}
\]
Với công thức này, chúng ta có thể xác định tốc độ và hướng chuyển động của vật thể tại bất kỳ thời điểm nào. Đạo hàm vận tốc giúp làm rõ sự thay đổi của vị trí theo thời gian, cung cấp cái nhìn chi tiết về hành vi của vật thể trong quá trình chuyển động.
Vận tốc có thể là một hằng số trong trường hợp chuyển động thẳng đều, hoặc là một hàm số phức tạp hơn trong các trường hợp chuyển động có gia tốc. Trong vật lý, đạo hàm vận tốc còn giúp xác định các đại lượng quan trọng khác như gia tốc và động lượng, tạo nền tảng cho nhiều ứng dụng trong các ngành khoa học và kỹ thuật.
Đạo hàm vận tốc không chỉ là một công cụ toán học, mà còn là phương tiện quan trọng để hiểu và mô tả thế giới xung quanh chúng ta, từ các hiện tượng tự nhiên như rơi tự do, đến các ứng dụng công nghệ hiện đại như thiết kế ô tô và máy bay.
2. Công Thức Đạo Hàm Vận Tốc
Công thức đạo hàm vận tốc là một phần quan trọng trong việc phân tích chuyển động của các vật thể. Vận tốc, được biểu diễn bằng đạo hàm của vị trí theo thời gian, có thể được tính toán thông qua các công thức cụ thể tùy thuộc vào dạng của hàm vị trí. Dưới đây là một số công thức đạo hàm vận tốc thường gặp.
2.1 Công Thức Tổng Quát
Giả sử \(s(t)\) là hàm vị trí của một vật thể theo thời gian \(t\), thì vận tốc tức thời \(v(t)\) được xác định bằng:
\[
v(t) = \frac{ds(t)}{dt}
\]
Công thức này mô tả vận tốc tức thời tại bất kỳ thời điểm \(t\) nào, phản ánh sự thay đổi của vị trí \(s(t)\) theo thời gian.
2.2 Đạo Hàm Vận Tốc Cho Một Số Hàm Vị Trí Thường Gặp
- Hàm vị trí bậc nhất: Nếu \(s(t) = at + b\), thì vận tốc là hằng số và được tính như sau:
- Hàm vị trí bậc hai: Nếu \(s(t) = at^2 + bt + c\), thì vận tốc sẽ thay đổi tuyến tính theo thời gian:
- Hàm vị trí bậc ba: Nếu \(s(t) = at^3 + bt^2 + ct + d\), vận tốc sẽ được tính bằng:
- Hàm vị trí hàm mũ: Nếu \(s(t) = ae^{bt}\), thì vận tốc sẽ tỷ lệ với hàm mũ theo thời gian:
\[
v(t) = a
\]
\[
v(t) = 2at + b
\]
\[
v(t) = 3at^2 + 2bt + c
\]
\[
v(t) = abe^{bt}
\]
2.3 Bảng Tổng Hợp Công Thức Đạo Hàm Vận Tốc
| Hàm Vị Trí \(s(t)\) | Vận Tốc \(v(t)\) | Đặc Điểm |
|---|---|---|
| \(s(t) = at + b\) | \(v(t) = a\) | Vận tốc không đổi, chuyển động thẳng đều. |
| \(s(t) = at^2 + bt + c\) | \(v(t) = 2at + b\) | Vận tốc thay đổi tuyến tính theo thời gian. |
| \(s(t) = at^3 + bt^2 + ct + d\) | \(v(t) = 3at^2 + 2bt + c\) | Vận tốc thay đổi theo hàm bậc hai của thời gian. |
| \(s(t) = ae^{bt}\) | \(v(t) = abe^{bt}\) | Vận tốc tỷ lệ với hàm mũ theo thời gian. |
Các công thức trên cung cấp cơ sở để tính toán vận tốc dựa trên hàm vị trí cụ thể, giúp phân tích chuyển động một cách chính xác và hiệu quả.

3. Ví Dụ Minh Họa Đạo Hàm Vận Tốc
Để hiểu rõ hơn về đạo hàm vận tốc và ứng dụng của nó, chúng ta sẽ đi qua một số ví dụ minh họa cụ thể. Các ví dụ này sẽ giúp bạn thấy cách tính toán và phân tích vận tốc từ các hàm vị trí khác nhau trong các tình huống thực tế.
3.1 Ví Dụ 1: Vật Rơi Tự Do
Giả sử một vật thể được thả rơi tự do từ độ cao \(h_0\) so với mặt đất. Vị trí của vật thể theo thời gian được mô tả bởi phương trình:
\[
s(t) = h_0 - \frac{1}{2}gt^2
\]
Trong đó:
- \(s(t)\) là độ cao của vật thể tại thời điểm \(t\).
- \(g\) là gia tốc trọng trường (khoảng \(9.8 \, \text{m/s}^2\)).
Để tìm vận tốc tức thời \(v(t)\) của vật thể tại thời điểm \(t\), ta tính đạo hàm của \(s(t)\) theo \(t\):
\[
v(t) = \frac{ds(t)}{dt} = -gt
\]
Vận tốc này là một hàm tuyến tính theo thời gian, cho thấy rằng vật thể tăng tốc đều khi rơi.
3.2 Ví Dụ 2: Chuyển Động Thẳng Đều
Giả sử một ô tô di chuyển thẳng với vận tốc không đổi \(v_0\). Vị trí của ô tô tại thời điểm \(t\) được mô tả bởi phương trình:
\[
s(t) = v_0t + s_0
\]
Trong đó:
- \(s_0\) là vị trí ban đầu của ô tô tại thời điểm \(t = 0\).
- \(v_0\) là vận tốc không đổi.
Vì vận tốc là hằng số, đạo hàm của \(s(t)\) theo \(t\) sẽ cho ra:
\[
v(t) = \frac{ds(t)}{dt} = v_0
\]
Điều này chứng tỏ rằng vận tốc của ô tô không thay đổi theo thời gian, và chuyển động của nó là chuyển động thẳng đều.
3.3 Ví Dụ 3: Chuyển Động Với Gia Tốc Không Đổi
Giả sử một vật thể di chuyển với gia tốc không đổi \(a\), vị trí của vật thể theo thời gian được mô tả bởi phương trình:
\[
s(t) = \frac{1}{2}at^2 + v_0t + s_0
\]
Trong đó:
- \(a\) là gia tốc không đổi.
- \(v_0\) là vận tốc ban đầu.
- \(s_0\) là vị trí ban đầu của vật thể tại thời điểm \(t = 0\).
Để tìm vận tốc tức thời \(v(t)\) của vật thể tại thời điểm \(t\), ta tính đạo hàm của \(s(t)\) theo \(t\):
\[
v(t) = \frac{ds(t)}{dt} = at + v_0
\]
Điều này cho thấy vận tốc của vật thể tăng dần theo thời gian, phù hợp với chuyển động có gia tốc không đổi.

4. Ứng Dụng Thực Tế của Đạo Hàm Vận Tốc
Đạo hàm vận tốc không chỉ là một công cụ toán học mà còn có nhiều ứng dụng thực tế trong các lĩnh vực khác nhau như vật lý, kỹ thuật, và kinh tế. Các ứng dụng này giúp chúng ta hiểu rõ hơn về cách các hệ thống hoạt động, tối ưu hóa quy trình, và dự đoán kết quả trong tương lai.
4.1 Ứng Dụng Trong Vật Lý và Kỹ Thuật
- Chuyển động của vật thể: Đạo hàm vận tốc được sử dụng để phân tích chuyển động của các vật thể trong không gian, từ các hạt nhỏ bé trong vật lý hạt nhân đến các hành tinh trong thiên văn học. Nó giúp xác định vị trí và vận tốc của các vật thể tại bất kỳ thời điểm nào.
- Thiết kế phương tiện giao thông: Trong ngành kỹ thuật, đạo hàm vận tốc là yếu tố quan trọng trong việc thiết kế và thử nghiệm các phương tiện như ô tô, tàu hỏa, máy bay, đảm bảo chúng hoạt động hiệu quả và an toàn trong quá trình di chuyển.
- Phân tích dòng chảy: Trong kỹ thuật chất lỏng, đạo hàm vận tốc giúp mô tả dòng chảy của chất lỏng qua các ống dẫn hoặc kênh, từ đó tối ưu hóa thiết kế của các hệ thống cung cấp nước và xử lý chất thải.
4.2 Ứng Dụng Trong Kinh Tế
- Dự đoán biến động giá: Đạo hàm vận tốc được sử dụng trong kinh tế để dự đoán sự thay đổi của giá cả hoặc chỉ số tài chính theo thời gian. Điều này giúp các nhà đầu tư đưa ra quyết định chính xác trong việc mua bán chứng khoán.
- Phân tích tăng trưởng: Đạo hàm vận tốc có thể được áp dụng để phân tích tốc độ tăng trưởng của các chỉ số kinh tế như GDP, giúp các nhà hoạch định chính sách đánh giá tình hình kinh tế và đưa ra các biện pháp phù hợp.
4.3 Ứng Dụng Trong Các Lĩnh Vực Khác
- Y học: Đạo hàm vận tốc được sử dụng trong y học để theo dõi sự thay đổi của các chỉ số sinh học theo thời gian, chẳng hạn như tốc độ truyền dịch trong cơ thể, giúp cải thiện quá trình điều trị và chăm sóc bệnh nhân.
- Khoa học môi trường: Trong lĩnh vực môi trường, đạo hàm vận tốc giúp phân tích sự thay đổi của các yếu tố môi trường như mức độ ô nhiễm không khí hoặc nước, từ đó đề ra các giải pháp bảo vệ môi trường hiệu quả.
Các ứng dụng trên chỉ là một vài ví dụ điển hình về cách đạo hàm vận tốc được sử dụng trong cuộc sống hàng ngày. Nhờ vào tính linh hoạt và khả năng ứng dụng rộng rãi, đạo hàm vận tốc đã trở thành một công cụ không thể thiếu trong nhiều lĩnh vực khoa học và kỹ thuật.

5. Bảng Tổng Hợp Các Công Thức Đạo Hàm Vận Tốc
Dưới đây là bảng tổng hợp các công thức quan trọng liên quan đến đạo hàm vận tốc. Những công thức này được áp dụng rộng rãi trong các bài toán vật lý và kỹ thuật để xác định vận tốc tức thời của một vật thể trong chuyển động. Mỗi công thức thể hiện cách tính vận tốc từ hàm vị trí theo thời gian, với các biến và tham số cụ thể.
| Công Thức | Diễn Giải |
|---|---|
| \[v(t) = \frac{ds(t)}{dt}\] | Vận tốc tức thời là đạo hàm của hàm vị trí \(s(t)\) theo thời gian \(t\). |
| \[v(t) = v_0 + at\] | Vận tốc của vật thể trong chuyển động thẳng có gia tốc không đổi, với \(v_0\) là vận tốc ban đầu và \(a\) là gia tốc. |
| \[v(t) = -gt\] | Vận tốc của vật thể rơi tự do dưới tác động của trọng lực, với \(g\) là gia tốc trọng trường. |
| \[v(t) = \omega r\] | Vận tốc tuyến tính của một điểm trên vòng tròn với \(r\) là bán kính và \(\omega\) là tốc độ góc. |
| \[v(t) = \frac{k}{m}t\] | Vận tốc trong trường hợp lực tác dụng là hàm tuyến tính theo thời gian, với \(k\) là hệ số và \(m\) là khối lượng. |
| \[v(t) = v_0 e^{-\frac{t}{\tau}}\] | Vận tốc giảm dần theo thời gian trong một hệ có lực ma sát, với \(v_0\) là vận tốc ban đầu và \(\tau\) là hằng số thời gian. |
Bảng trên cung cấp một cái nhìn tổng quan về các công thức cơ bản để tính vận tốc từ các hàm vị trí khác nhau. Hiểu rõ và vận dụng linh hoạt các công thức này sẽ giúp giải quyết các bài toán thực tế liên quan đến chuyển động một cách hiệu quả.
XEM THÊM:
6. Tài Liệu Tham Khảo và Học Tập
Để nắm vững khái niệm đạo hàm vận tốc và ứng dụng của nó, bạn có thể tham khảo một số tài liệu và nguồn học tập đáng tin cậy dưới đây. Các tài liệu này bao gồm sách giáo khoa, bài giảng trực tuyến, và các trang web chuyên sâu về toán học và vật lý. Đây sẽ là nguồn tài liệu hữu ích cho cả học sinh, sinh viên và những người đam mê khoa học.
6.1 Sách Giáo Khoa và Tài Liệu In
- Sách Giáo Khoa Toán Học Lớp 12: Cuốn sách này cung cấp kiến thức cơ bản và nâng cao về đạo hàm và các ứng dụng của nó trong bài toán vận tốc, phù hợp cho học sinh trung học phổ thông.
- Giải Tích 1 - Trường Đại Học Sư Phạm Hà Nội: Cuốn sách chuyên sâu dành cho sinh viên đại học với các bài tập vận dụng đạo hàm trong tính toán vận tốc và nhiều bài toán khác liên quan.
- Physics for Scientists and Engineers - Serway: Một cuốn sách quốc tế nổi tiếng, cung cấp cách tiếp cận toàn diện về vận tốc trong vật lý với sự hỗ trợ của đạo hàm và các phương pháp tính toán khác.
6.2 Bài Giảng Trực Tuyến và Video
- Khan Academy: Trang web cung cấp các bài giảng video miễn phí về toán học và vật lý, trong đó có chuyên đề về đạo hàm và ứng dụng trong việc tính toán vận tốc.
- Coursera - Calculus Courses: Các khóa học online về Giải tích với nhiều bài học chi tiết về đạo hàm và ứng dụng trong vật lý, đặc biệt là trong phân tích vận tốc.
- Học Mãi: Một nền tảng giáo dục trực tuyến phổ biến tại Việt Nam, cung cấp các bài giảng về toán học cấp 3 với phần học về đạo hàm và bài toán vận tốc.
6.3 Trang Web và Blog Học Thuật
- Wikipedia - Derivative: Bài viết cung cấp cái nhìn tổng quan về đạo hàm, định nghĩa và các ứng dụng của nó, bao gồm cả trong việc tính vận tốc.
- Math is Fun: Trang web này giúp bạn học toán một cách dễ hiểu với các ví dụ minh họa trực quan về đạo hàm và vận tốc.
- Vật Lý Việt Nam: Một blog cung cấp kiến thức vật lý căn bản và nâng cao, với nhiều bài viết về cách sử dụng đạo hàm để giải các bài toán liên quan đến chuyển động.
Những tài liệu và nguồn tham khảo trên đây sẽ giúp bạn củng cố kiến thức về đạo hàm vận tốc, cũng như áp dụng chúng vào thực tế một cách hiệu quả. Việc học tập từ nhiều nguồn khác nhau sẽ giúp bạn có cái nhìn toàn diện và sâu sắc hơn về chủ đề này.