Viết Phương Trình Li Độ, Vận Tốc, Gia Tốc: Hướng Dẫn Chi Tiết và Ứng Dụng

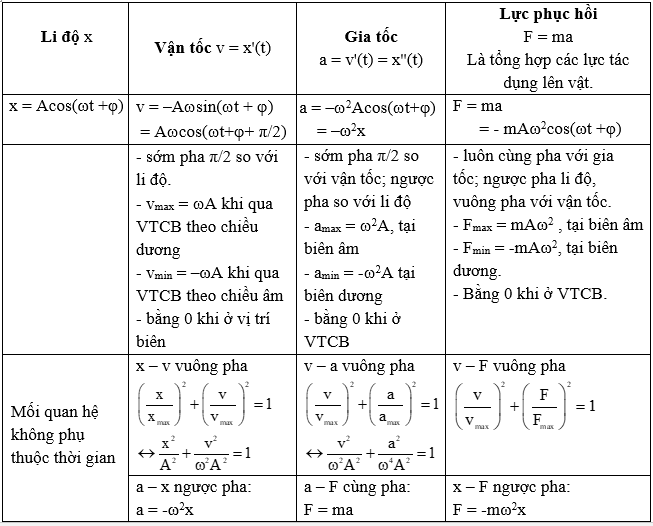
Trong dao động điều hòa, phương trình của li độ, vận tốc và gia tốc là những yếu tố quan trọng giúp xác định trạng thái của vật theo thời gian. Các phương trình này phụ thuộc vào các đại lượng như biên độ dao động, tần số góc, pha ban đầu, và thời gian.

1. Phương trình li độ

Li độ \(x(t)\) của một vật dao động điều hòa tại thời điểm \(t\) được xác định theo công thức:

\[
x(t) = A \cos(\omega t + \varphi)
\]

Trong đó:

• \(A\): Biên độ dao động (là giá trị cực đại của li độ).
• \(\omega\): Tần số góc, có liên hệ với chu kỳ \(T\) và tần số \(f\) qua \(\omega = 2\pi f = \frac{2\pi}{T}\).
• \(\varphi\): Pha ban đầu, phụ thuộc vào điều kiện ban đầu của dao động.
• \(t\): Thời gian.

2. Phương trình vận tốc

Vận tốc \(v(t)\) của vật được xác định bằng đạo hàm bậc nhất của li độ theo thời gian:

\[
v(t) = \frac{dx(t)}{dt} = -A \omega \sin(\omega t + \varphi)
\]

Trong đó, vận tốc có thể dương hoặc âm, tương ứng với hướng chuyển động của vật.

3. Phương trình gia tốc

Gia tốc \(a(t)\) của vật là đạo hàm bậc nhất của vận tốc theo thời gian hoặc đạo hàm bậc hai của li độ theo thời gian:

\[
a(t) = \frac{dv(t)}{dt} = \frac{d^2x(t)}{dt^2} = -A \omega^2 \cos(\omega t + \varphi)
\]

Gia tốc có cùng pha với li độ nhưng ngược dấu, và có giá trị cực đại tại các vị trí biên của dao động.

4. Mối quan hệ giữa li độ, vận tốc và gia tốc

Trong dao động điều hòa, li độ, vận tốc và gia tốc có mối quan hệ mật thiết với nhau. Đặc biệt:

• Khi vật ở vị trí cân bằng \((x = 0)\), vận tốc đạt giá trị cực đại, và gia tốc bằng 0.
• Khi vật ở vị trí biên \((x = \pm A)\), vận tốc bằng 0, và gia tốc đạt giá trị cực đại với dấu ngược lại so với li độ.

Kết luận

Các phương trình li độ, vận tốc và gia tốc trong dao động điều hòa giúp mô tả chi tiết và chính xác trạng thái chuyển động của vật theo thời gian. Hiểu rõ mối quan hệ giữa các đại lượng này giúp giải quyết nhiều bài toán vật lý phức tạp một cách dễ dàng.

Dao động điều hòa là một dạng chuyển động quan trọng trong vật lý, mô tả sự chuyển động lặp đi lặp lại của một vật quanh vị trí cân bằng. Đặc điểm chính của dao động điều hòa là biên độ không đổi và chuyển động diễn ra theo một quỹ đạo hình sin hoặc cosin.

Trong dao động điều hòa, có ba đại lượng quan trọng cần phải xác định: li độ, vận tốc và gia tốc. Các đại lượng này không chỉ xác định vị trí tức thời của vật mà còn cung cấp thông tin về chuyển động của vật theo thời gian.

Một dao động điều hòa được đặc trưng bởi các thông số chính:

• Biên độ \((A)\): Là giá trị cực đại của li độ, biểu thị mức độ dao động của vật so với vị trí cân bằng.
• Tần số góc \((\omega)\): Là tốc độ góc quay, liên hệ với chu kỳ \(T\) và tần số \(f\) qua công thức \(\omega = 2\pi f = \frac{2\pi}{T}\).
• Pha ban đầu \((\varphi)\): Là giá trị của pha tại thời điểm ban đầu \(t = 0\), xác định trạng thái dao động của vật.

Phương trình tổng quát của dao động điều hòa được biểu diễn dưới dạng:

\[
x(t) = A \cos(\omega t + \varphi)
\]

Trong đó:

• \(x(t)\) là li độ của vật tại thời điểm \(t\).
• \(A\) là biên độ dao động.
• \(\omega\) là tần số góc.
• \(\varphi\) là pha ban đầu.

Với phương trình này, ta có thể tính toán các giá trị li độ, vận tốc và gia tốc của vật tại bất kỳ thời điểm nào trong quá trình dao động, từ đó phân tích chính xác trạng thái của vật.

Phương trình li độ trong dao động điều hòa là một trong những phương trình cơ bản mô tả chuyển động của vật. Li độ \(x(t)\) cho biết vị trí tức thời của vật so với vị trí cân bằng, và được xác định bởi các thông số như biên độ, tần số góc và pha ban đầu.

Phương trình tổng quát của li độ trong dao động điều hòa được viết dưới dạng:

\[
x(t) = A \cos(\omega t + \varphi)
\]

Trong đó:

• \(x(t)\): Li độ tại thời điểm \(t\), biểu thị khoảng cách từ vị trí của vật đến vị trí cân bằng.
• \(A\): Biên độ dao động, đại diện cho giá trị cực đại của li độ.
• \(\omega\): Tần số góc, là tốc độ góc của dao động và được tính bằng \(\omega = 2\pi f = \frac{2\pi}{T}\), trong đó \(f\) là tần số và \(T\) là chu kỳ.
• \(\varphi\): Pha ban đầu, xác định trạng thái ban đầu của dao động khi \(t = 0\).

Phương trình này cho phép ta xác định vị trí của vật tại bất kỳ thời điểm nào trong quá trình dao động. Khi \(\varphi = 0\), phương trình trở thành:

\[
x(t) = A \cos(\omega t)
\]

Điều này có nghĩa là tại thời điểm \(t = 0\), vật bắt đầu dao động từ vị trí biên với li độ cực đại \(A\). Nếu \(\varphi\) khác 0, pha ban đầu sẽ làm thay đổi điểm bắt đầu của dao động, dẫn đến việc vật không ở vị trí biên khi bắt đầu chuyển động.

Việc hiểu rõ phương trình li độ là nền tảng để nắm bắt các hiện tượng dao động khác, như vận tốc và gia tốc, bởi các đại lượng này đều liên quan chặt chẽ đến li độ. Phân tích phương trình li độ giúp ta dễ dàng tính toán và dự đoán chuyển động của vật theo thời gian.

Trong dao động điều hòa, vận tốc của vật là đại lượng biến thiên tuần hoàn theo thời gian. Phương trình vận tốc của một vật dao động điều hòa có dạng:

\[v(t) = -\omega A \sin(\omega t + \varphi)\]

Trong đó:

• \(v(t)\): Vận tốc tại thời điểm \(t\)
• \(\omega\): Tần số góc của dao động, được tính bằng công thức \(\omega = 2\pi f\), với \(f\) là tần số dao động
• \(A\): Biên độ dao động, là giá trị lớn nhất của li độ
• \(\varphi\): Pha ban đầu của dao động

Khi vật đi qua vị trí cân bằng, vận tốc đạt giá trị lớn nhất và bằng \(v_{\text{max}} = \omega A\). Tại vị trí biên, vận tốc của vật bằng không.

Đồ thị biểu diễn sự biến đổi của vận tốc theo thời gian có dạng hình sin, tương tự như đồ thị của li độ nhưng lệch pha \(\frac{\pi}{2}\) (sớm pha hơn li độ).

Gia tốc trong dao động điều hòa là đại lượng vật lý quan trọng mô tả sự biến đổi của vận tốc theo thời gian. Gia tốc có vai trò quyết định đến sự thay đổi hướng và độ lớn của vận tốc. Phương trình gia tốc trong dao động điều hòa được xác định từ đạo hàm bậc hai của phương trình li độ theo thời gian:

\[a(t) = -\omega^2 x(t)\]

Thay thế \(x(t)\) từ phương trình li độ vào, ta có phương trình gia tốc:

\[a(t) = -\omega^2 A \cos(\omega t + \varphi)\]

Trong đó:

• \(a(t)\): Gia tốc tại thời điểm \(t\)
• \(\omega\): Tần số góc của dao động
• \(A\): Biên độ dao động
• \(\varphi\): Pha ban đầu của dao động

Gia tốc trong dao động điều hòa có những đặc điểm sau:

• Gia tốc đạt giá trị cực đại khi vật ở vị trí biên và bằng \(\pm \omega^2 A\).
• Gia tốc bằng 0 khi vật đi qua vị trí cân bằng.
• Gia tốc luôn hướng về vị trí cân bằng, nghĩa là ngược pha với li độ.

Đồ thị biểu diễn sự biến đổi của gia tốc theo thời gian cũng có dạng hình sin, lệch pha \(\pi\) so với đồ thị của li độ. Điều này cho thấy khi vật ở vị trí biên (li độ lớn nhất), gia tốc đạt giá trị cực đại và ngược lại.

Trong dao động điều hòa, li độ, vận tốc và gia tốc là ba đại lượng vật lý liên quan chặt chẽ với nhau. Chúng được mô tả bằng các phương trình toán học và có sự tương quan pha theo thời gian.

Mối quan hệ giữa li độ \(x(t)\), vận tốc \(v(t)\) và gia tốc \(a(t)\) được xác định bởi các phương trình sau:

• Li độ: \[x(t) = A \cos(\omega t + \varphi)\]
• Vận tốc: \[v(t) = -\omega A \sin(\omega t + \varphi)\]
• Gia tốc: \[a(t) = -\omega^2 A \cos(\omega t + \varphi)\]

Những đặc điểm quan trọng của mối quan hệ này bao gồm:

• Vận tốc là đạo hàm bậc nhất của li độ theo thời gian: \[v(t) = \frac{dx(t)}{dt}\]
• Gia tốc là đạo hàm bậc hai của li độ theo thời gian: \[a(t) = \frac{d^2x(t)}{dt^2}\]
• Gia tốc ngược pha với li độ và cùng pha với vận tốc, nhưng có độ lớn khác nhau.
• Khi li độ đạt giá trị cực đại (ở vị trí biên), vận tốc bằng 0 và gia tốc đạt giá trị cực đại.
• Khi vật đi qua vị trí cân bằng (li độ bằng 0), vận tốc đạt giá trị cực đại và gia tốc bằng 0.

Để hiểu rõ hơn, ta có thể hình dung rằng vận tốc và gia tốc trong dao động điều hòa luôn dao động quanh li độ, tạo ra các trạng thái dao động tuần hoàn, liên tục và hài hòa.

Để nắm vững kiến thức về dao động điều hòa, việc luyện tập với các bài tập và ví dụ minh họa là rất quan trọng. Dưới đây là một số bài tập mẫu và ví dụ cụ thể để giúp bạn củng cố và ứng dụng các phương trình đã học.

Ví dụ 1: Tính li độ, vận tốc và gia tốc tại một thời điểm

Giả sử một vật dao động điều hòa với biên độ \(A = 5 \, \text{cm}\), tần số góc \(\omega = 2 \, \text{rad/s}\), pha ban đầu \(\varphi = \frac{\pi}{4}\). Hãy tính li độ, vận tốc và gia tốc của vật tại thời điểm \(t = 2 \, \text{s}\).

Giải:

• Li độ: \[x(2) = 5 \cos\left(2 \times 2 + \frac{\pi}{4}\right) \approx 3.54 \, \text{cm}\]
• Vận tốc: \[v(2) = -2 \times 5 \sin\left(2 \times 2 + \frac{\pi}{4}\right) \approx -7.07 \, \text{cm/s}\]
• Gia tốc: \[a(2) = -2^2 \times 5 \cos\left(2 \times 2 + \frac{\pi}{4}\right) \approx -14.14 \, \text{cm/s}^2\]

Ví dụ 2: Xác định thời điểm vật đạt vận tốc cực đại

Vật dao động điều hòa với phương trình vận tốc \(v(t) = -\omega A \sin(\omega t + \varphi)\). Xác định thời điểm khi vận tốc đạt giá trị cực đại.

Giải:

• Vận tốc cực đại xảy ra khi \(\sin(\omega t + \varphi) = \pm 1\).
• Tại thời điểm này, \(v_{\text{max}} = \omega A\) và thời điểm đạt vận tốc cực đại là \[t = \frac{(2k+1)\pi}{2\omega} - \frac{\varphi}{\omega}\] với \(k\) là số nguyên.

Bài tập tự luyện

Dưới đây là một số bài tập tự luyện để giúp bạn kiểm tra và củng cố kiến thức:

1. Cho phương trình dao động \(x(t) = 10 \cos(3t + \frac{\pi}{6})\). Hãy xác định tần số góc, chu kỳ dao động, và thời điểm vật qua vị trí cân bằng lần đầu tiên.
2. Một vật dao động với biên độ \(A = 8 \, \text{cm}\) và tần số góc \(\omega = 4 \, \text{rad/s}\). Tính vận tốc và gia tốc của vật tại vị trí li độ bằng một nửa biên độ.
3. Hãy vẽ đồ thị biểu diễn sự biến đổi của li độ, vận tốc và gia tốc theo thời gian cho dao động có phương trình \(x(t) = 6 \cos(2t - \frac{\pi}{3})\).