So sánh vận tốc và tốc độ: Khái niệm, công thức và ứng dụng thực tiễn

Trong vật lý học, vận tốc và tốc độ là hai khái niệm quan trọng nhưng có sự khác biệt rõ rệt. Dưới đây là so sánh chi tiết giữa hai khái niệm này:

Định nghĩa

• Tốc độ: Là đại lượng vô hướng, cho biết quãng đường một vật di chuyển được trong một đơn vị thời gian. Công thức tính tốc độ là \[ v = \frac{s}{t} \], trong đó \( s \) là quãng đường và \( t \) là thời gian.
• Vận tốc: Là đại lượng vector, không chỉ bao gồm độ lớn mà còn cả hướng của sự di chuyển. Công thức tính vận tốc là \[ \vec{v} = \frac{\vec{d}}{t} \], trong đó \( \vec{d} \) là độ dịch chuyển (bao gồm cả hướng) và \( t \) là thời gian.

Đặc điểm

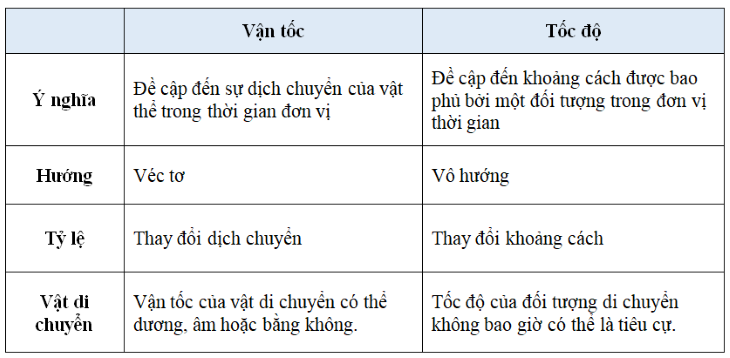
• Đại lượng: Tốc độ là đại lượng vô hướng, trong khi vận tốc là đại lượng vector.
• Giá trị: Tốc độ luôn dương hoặc bằng 0, còn vận tốc có thể âm, dương hoặc bằng 0 tùy vào hướng di chuyển.

Tính toán

Để tính tốc độ trung bình, ta lấy tổng quãng đường di chuyển chia cho tổng thời gian di chuyển. Trong khi đó, vận tốc trung bình được tính bằng độ dịch chuyển chia cho tổng thời gian di chuyển.

Sự khác biệt chính

• Tốc độ chỉ biểu thị mức độ nhanh chóng của chuyển động mà không quan tâm đến hướng, trong khi vận tốc biểu thị cả tốc độ và hướng của chuyển động.
• Tốc độ là một đại lượng vô hướng và không thể có giá trị âm, trong khi vận tốc là đại lượng vector và có thể có giá trị âm tùy thuộc vào hướng di chuyển.

Kết luận

Sự khác biệt giữa vận tốc và tốc độ chủ yếu nằm ở yếu tố hướng. Trong các bài toán vật lý, việc hiểu rõ và áp dụng đúng khái niệm vận tốc và tốc độ là rất quan trọng để giải quyết các vấn đề liên quan đến chuyển động của vật thể.

Trong vật lý học, tốc độ và vận tốc là hai khái niệm quan trọng dùng để mô tả chuyển động của vật thể. Dưới đây là định nghĩa và khái niệm cơ bản về chúng:

• Tốc độ: Tốc độ là đại lượng vô hướng, chỉ đơn thuần mô tả độ nhanh của chuyển động mà không quan tâm đến hướng. Công thức tính tốc độ là \[ v = \frac{s}{t} \], trong đó \( s \) là quãng đường di chuyển và \( t \) là thời gian di chuyển.
• Vận tốc: Vận tốc là đại lượng vector, không chỉ mô tả độ nhanh của chuyển động mà còn bao gồm cả hướng di chuyển. Công thức tính vận tốc là \[ \vec{v} = \frac{\vec{d}}{t} \], trong đó \( \vec{d} \) là độ dịch chuyển theo hướng xác định và \( t \) là thời gian di chuyển.

Sự khác biệt cơ bản giữa tốc độ và vận tốc nằm ở yếu tố hướng: tốc độ chỉ đo lường độ lớn của sự di chuyển, trong khi vận tốc đo lường cả độ lớn và hướng di chuyển.

Cả vận tốc và tốc độ đều có những công thức tính và đơn vị đo riêng biệt, giúp xác định mức độ nhanh chậm của chuyển động. Dưới đây là các công thức và đơn vị tương ứng cho từng khái niệm:

• Tốc độ trung bình:

Tốc độ trung bình được tính bằng công thức:

\[ v = \frac{s}{t} \]

Trong đó:

• \(v\): Tốc độ trung bình (đơn vị: m/s hoặc km/h)
• \(s\): Quãng đường đi được (đơn vị: mét hoặc kilômét)
• \(t\): Thời gian di chuyển (đơn vị: giây hoặc giờ)

Đơn vị đo của tốc độ thường là mét trên giây (m/s) hoặc kilômét trên giờ (km/h). Mối quan hệ giữa các đơn vị này được biểu diễn như sau:

\[ 1 \text{ m/s} = 3.6 \text{ km/h} \]
• Vận tốc trung bình:

Vận tốc trung bình được tính bằng công thức:

\[ v_{\text{tb}} = \frac{\Delta x}{\Delta t} \]

Trong đó:

• \(v_{\text{tb}}\): Vận tốc trung bình (đơn vị: m/s)
• \(\Delta x\): Độ dịch chuyển (đơn vị: mét)
• \(\Delta t\): Thời gian dịch chuyển (đơn vị: giây)

Đơn vị đo của vận tốc thường là mét trên giây (m/s).

Tóm lại, cả tốc độ và vận tốc đều là những khái niệm quan trọng trong vật lý, tuy nhiên, vận tốc là một đại lượng vectơ, bao gồm cả độ lớn và hướng, trong khi tốc độ chỉ là một đại lượng vô hướng, chỉ xét đến độ lớn.

Vận tốc và tốc độ là hai khái niệm quan trọng trong vật lý học, tuy nhiên, chúng có sự khác biệt rõ rệt về cả mặt định nghĩa và tính chất. Dưới đây là những điểm khác biệt chính giữa vận tốc và tốc độ:

• Định nghĩa:
• Tốc độ: Tốc độ là một đại lượng vô hướng, chỉ biểu thị độ lớn của chuyển động mà không quan tâm đến hướng di chuyển. Tốc độ cho biết quãng đường mà một vật đi được trong một khoảng thời gian nhất định.
• Vận tốc: Vận tốc là một đại lượng vectơ, nghĩa là nó có cả độ lớn và hướng. Vận tốc không chỉ cho biết tốc độ mà còn cho biết hướng di chuyển của vật.
• Công thức tính:
• Tốc độ: Công thức tính tốc độ là:
\[ v = \frac{s}{t} \]

Trong đó \(v\) là tốc độ, \(s\) là quãng đường, và \(t\) là thời gian.

• Vận tốc: Công thức tính vận tốc là:
\[ \vec{v} = \frac{\Delta \vec{x}}{\Delta t} \]

Trong đó \(\vec{v}\) là vận tốc, \(\Delta \vec{x}\) là độ dịch chuyển, và \(\Delta t\) là thời gian.

• Đơn vị đo:
• Tốc độ: Đơn vị đo tốc độ thường là mét trên giây (m/s) hoặc kilômét trên giờ (km/h).
• Vận tốc: Đơn vị đo vận tốc cũng là mét trên giây (m/s), nhưng vì nó là một đại lượng vectơ, nên cần biểu diễn cả hướng.
• Tính chất:
• Tốc độ: Tốc độ luôn luôn là số dương hoặc bằng không, vì nó chỉ đo lường độ lớn của quãng đường di chuyển.
• Vận tốc: Vận tốc có thể là số dương, âm, hoặc bằng không, tùy thuộc vào hướng di chuyển của vật so với hệ quy chiếu ban đầu.
• Ý nghĩa thực tế:
• Tốc độ: Tốc độ chỉ quan tâm đến việc một vật đi được bao xa trong một khoảng thời gian mà không quan tâm nó di chuyển theo hướng nào.
• Vận tốc: Vận tốc cung cấp thông tin toàn diện hơn, bao gồm cả tốc độ và hướng, giúp xác định chính xác vị trí của vật trong không gian.

Tóm lại, sự khác biệt lớn nhất giữa vận tốc và tốc độ nằm ở chỗ vận tốc là một đại lượng vectơ có hướng, trong khi tốc độ chỉ là một đại lượng vô hướng không có hướng.

Vận tốc và tốc độ là những khái niệm quan trọng không chỉ trong lĩnh vực vật lý mà còn có nhiều ứng dụng thực tế trong đời sống hàng ngày. Hiểu rõ về chúng giúp chúng ta giải quyết hiệu quả các vấn đề liên quan đến chuyển động và định hướng. Dưới đây là một số ứng dụng cụ thể:

• Trong giao thông vận tải:

  • Quản lý tốc độ: Tốc độ được sử dụng để xác định mức độ nhanh chậm của các phương tiện như ô tô, xe máy, tàu hỏa. Việc kiểm soát tốc độ giúp đảm bảo an toàn giao thông và tuân thủ luật lệ đường bộ.

  • Xác định thời gian di chuyển: Bằng cách biết tốc độ trung bình và quãng đường cần đi, chúng ta có thể tính toán thời gian dự kiến để đến đích bằng công thức:

    \[ t = \frac{s}{v} \]

    Trong đó:

    • \(t\): Thời gian di chuyển
    • \(s\): Quãng đường
    • \(v\): Tốc độ trung bình

    Điều này hỗ trợ trong việc lập kế hoạch hành trình một cách hiệu quả.

  • Định vị và dẫn đường: Vận tốc được sử dụng trong hệ thống GPS để xác định vị trí và hướng di chuyển của các phương tiện, giúp cung cấp chỉ dẫn đường đi chính xác.

• Trong thể thao:

  • Đánh giá hiệu suất vận động viên: Tốc độ và vận tốc được sử dụng để đo lường và phân tích hiệu suất của vận động viên trong các môn thể thao như điền kinh, bơi lội, đua xe, giúp cải thiện kỹ thuật và chiến lược thi đấu.

  • Phân tích chiến thuật: Việc hiểu rõ vận tốc giúp các huấn luyện viên xây dựng chiến thuật phù hợp dựa trên khả năng di chuyển và định hướng của vận động viên.

• Trong khoa học và kỹ thuật:

  • Thiết kế công trình: Vận tốc của gió và nước được xem xét khi thiết kế các công trình xây dựng như cầu, tòa nhà cao tầng để đảm bảo an toàn và ổn định.

  • Nghiên cứu chuyển động: Trong vật lý, vận tốc là yếu tố quan trọng trong việc nghiên cứu và mô phỏng các hiện tượng chuyển động, từ cấp độ hạt nhân đến thiên văn.

• Trong giải quyết bài toán vật lý:

  • Bài toán chuyển động thẳng đều: Sử dụng công thức vận tốc để tính toán các đại lượng liên quan:

    \[ v = \frac{\Delta x}{\Delta t} \]

    Ví dụ: Một vật di chuyển 100m trong 20 giây theo một hướng nhất định. Vận tốc của vật là:

    \[ v = \frac{100\,\text{m}}{20\,\text{s}} = 5\,\text{m/s} \]

  • Bài toán chuyển động biến đổi: Vận tốc và gia tốc được sử dụng để phân tích chuyển động có gia tốc, như chuyển động rơi tự do:

    \[ v = v_0 + a t \]

    Trong đó:

    • \(v_0\): Vận tốc ban đầu
    • \(a\): Gia tốc
    • \(t\): Thời gian

    Ví dụ: Một vật thả rơi tự do từ độ cao 20m. Sau 2 giây, vận tốc của vật là:

    \[ v = 0 + 9.8 \times 2 = 19.6\,\text{m/s} \]

  • Bài toán chuyển động tròn: Vận tốc tiếp tuyến và vận tốc góc được sử dụng để mô tả chuyển động của vật trên quỹ đạo tròn, như chuyển động của hành tinh quanh mặt trời.

Nhờ việc hiểu và áp dụng đúng các khái niệm về tốc độ và vận tốc, chúng ta có thể giải quyết hiệu quả nhiều vấn đề trong cuộc sống và khoa học, từ việc đơn giản như tính toán thời gian di chuyển đến những ứng dụng phức tạp trong kỹ thuật và nghiên cứu khoa học.