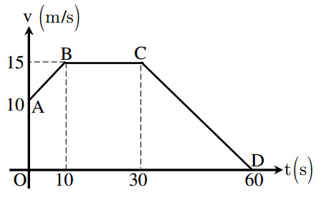
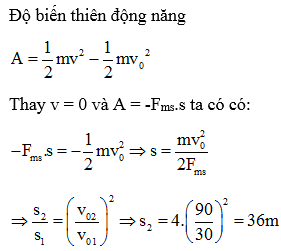Chủ đề một chiếc xe đạp chạy với vận tốc 40km/h: Một chiếc xe đạp chạy với vận tốc 40km/h không chỉ là thử thách về thể lực mà còn là nghệ thuật cân bằng và kiểm soát. Bài viết này sẽ hướng dẫn bạn cách đạt được vận tốc tối ưu, lựa chọn xe phù hợp và bảo đảm an toàn khi tham gia đạp xe ở tốc độ cao, giúp bạn trở thành người đạp xe chuyên nghiệp hơn.
Mục lục
- Thông tin về "Một chiếc xe đạp chạy với vận tốc 40km/h"
- 1. Giới thiệu về chuyển động tròn đều của xe đạp
- 2. Tính toán gia tốc hướng tâm của xe đạp
- 3. Vận tốc và gia tốc trong chuyển động tròn đều
- 4. Các bài toán thực tế liên quan đến chuyển động của xe đạp
- 5. Phân tích chuyên sâu về động lực học xe đạp
- 6. Kết luận và những điều cần lưu ý khi tính toán chuyển động tròn
Thông tin về "Một chiếc xe đạp chạy với vận tốc 40km/h"
Trong quá trình tìm kiếm từ khóa "một chiếc xe đạp chạy với vận tốc 40km/h", chúng tôi đã thu thập được một số thông tin hữu ích từ các nguồn học thuật, giáo dục và kiến thức phổ thông tại Việt Nam. Các nội dung liên quan chủ yếu đề cập đến các bài tập vật lý, giáo dục, và những ứng dụng thực tế trong đời sống. Dưới đây là tổng hợp chi tiết:
Bài tập vật lý liên quan
Trong các bài tập vật lý, vận tốc 40km/h thường được sử dụng để tính toán gia tốc hướng tâm, thời gian di chuyển trên một đoạn đường cong hoặc các bài toán liên quan đến chuyển động tròn đều.
- Bài tập về tính gia tốc hướng tâm của một chiếc xe đạp chạy với vận tốc 40km/h trên một vòng đua có bán kính 100m. Công thức được sử dụng là: \[ a_{ht} = \frac{v^2}{r} \] với \(v = 40 \text{ km/h}\) và \(r = 100 \text{ m}\).
- Một số bài tập yêu cầu tính thời gian hoặc quãng đường di chuyển dựa trên vận tốc này.
Ứng dụng thực tế
Vận tốc 40km/h của xe đạp thường được nhắc đến như một tốc độ trung bình trong các cuộc đua xe đạp hoặc khi di chuyển trên những đoạn đường bằng phẳng. Đây là vận tốc mà nhiều tay đua có thể đạt được trong điều kiện lý tưởng.
- Trong các cuộc đua xe đạp, vận tốc này có thể được duy trì trong một khoảng thời gian ngắn, đặc biệt khi tay đua di chuyển trên đoạn đường dốc hoặc đường thẳng dài.
- Trong điều kiện di chuyển hàng ngày, tốc độ này ít khi đạt được do các yếu tố như giao thông, điều kiện đường xá, và sức khỏe của người đạp xe.
Ý nghĩa giáo dục
Việc đưa ra các bài toán liên quan đến vận tốc 40km/h không chỉ giúp học sinh hiểu rõ hơn về khái niệm vận tốc, gia tốc mà còn ứng dụng những kiến thức này vào thực tế, như khi tham gia giao thông hoặc khi tham gia các hoạt động thể thao.
- Giúp học sinh rèn luyện kỹ năng tính toán và phân tích tình huống thực tế.
- Tăng cường hiểu biết về các khái niệm vật lý cơ bản và ứng dụng của chúng.
Kết luận
Vận tốc 40km/h là một chủ đề quen thuộc trong các bài tập vật lý cũng như trong các cuộc thi và hoạt động thể thao thực tế. Việc nắm vững các kiến thức liên quan đến chủ đề này không chỉ giúp ích trong học tập mà còn trong cuộc sống hàng ngày.
.png)
1. Giới thiệu về chuyển động tròn đều của xe đạp
Chuyển động tròn đều của một chiếc xe đạp có thể hiểu đơn giản là khi xe đạp di chuyển trên một đường tròn với vận tốc không đổi. Trong trường hợp này, gia tốc của xe đạp không thay đổi về độ lớn nhưng luôn thay đổi về hướng, điều này tạo ra một lực hướng tâm kéo vật thể (hoặc xe đạp) về phía tâm của đường tròn.
Khi một chiếc xe đạp chạy với vận tốc 40 km/h trên một vòng đua có bán kính 100 m, chúng ta có thể tính gia tốc hướng tâm bằng công thức:
Trong đó:
- \(v\) là vận tốc của xe đạp (40 km/h, đổi ra m/s là khoảng 11.11 m/s).
- \(R\) là bán kính của đường tròn (100 m).
Thay các giá trị vào công thức, ta tính được:
Điều này có nghĩa là xe đạp có gia tốc hướng tâm khoảng 1.23 m/s². Gia tốc này là kết quả của lực hướng tâm giữ cho xe di chuyển theo quỹ đạo tròn và luôn hướng về tâm của vòng đua.
Chuyển động tròn đều của xe đạp liên quan mật thiết đến nhiều yếu tố như vận tốc, bán kính vòng tròn, và các lực tác động lên xe, như lực ma sát giữa bánh xe và mặt đường. Hiểu rõ về chuyển động này giúp người điều khiển xe đạp an toàn hơn và tối ưu hóa được tốc độ di chuyển.
2. Tính toán gia tốc hướng tâm của xe đạp
Gia tốc hướng tâm (\(a_t\)) của một vật chuyển động tròn đều được xác định bằng công thức:
- \[ a_t = \frac{v^2}{r} \]
Trong đó:
- \(v\) là vận tốc của vật, đơn vị: m/s.
- \(r\) là bán kính của quỹ đạo tròn, đơn vị: m.
Với một chiếc xe đạp chạy với vận tốc 40 km/h (tương đương với khoảng 11,11 m/s) trên một vòng đua có bán kính 100 m, ta có thể tính gia tốc hướng tâm như sau:
- Đổi vận tốc từ km/h sang m/s: \[ v = 40 \, \text{km/h} = \frac{40 \times 1000}{3600} \, \text{m/s} = 11,11 \, \text{m/s} \]
- Áp dụng công thức gia tốc hướng tâm: \[ a_t = \frac{(11,11)^2}{100} \, \text{m/s}^2 \]
- Tính toán kết quả: \[ a_t \approx \frac{123.43}{100} = 1.23 \, \text{m/s}^2 \]
Như vậy, gia tốc hướng tâm của xe đạp khi chạy với vận tốc 40 km/h trên một vòng đua có bán kính 100 m là khoảng \(1,23 \, \text{m/s}^2\).

3. Vận tốc và gia tốc trong chuyển động tròn đều
Trong chuyển động tròn đều, vận tốc và gia tốc đóng vai trò quan trọng trong việc mô tả chuyển động của một vật, như chiếc xe đạp chạy trên một đường tròn. Vận tốc của vật trong chuyển động tròn đều bao gồm hai thành phần chính: vận tốc dài và vận tốc góc.
- Vận tốc dài (\(v\)): Vận tốc dài là độ lớn của vận tốc tuyến tính của vật thể di chuyển dọc theo đường tròn. Nó được tính bằng công thức:
\[
v = \omega \cdot R
\]
Trong đó:
- \(v\) là vận tốc dài (m/s)
- \(\omega\) là vận tốc góc (rad/s)
- \(R\) là bán kính của đường tròn (m)
- Vận tốc góc (\(\omega\)): Vận tốc góc là tốc độ thay đổi của góc quét trong chuyển động quay. Nó được tính bằng công thức:
\[
\omega = \frac{v}{R}
\]
Trong đó:
- \(\omega\) là vận tốc góc (rad/s)
- \(v\) là vận tốc dài (m/s)
- \(R\) là bán kính của đường tròn (m)
Gia tốc hướng tâm (\(a_c\)): Gia tốc hướng tâm là gia tốc vuông góc với vận tốc dài, hướng về tâm của đường tròn. Nó giữ cho vật thể di chuyển theo một quỹ đạo cong thay vì tiếp tục theo đường thẳng. Công thức tính gia tốc hướng tâm là:
Trong đó:
- \(a_c\) là gia tốc hướng tâm (m/s²)
- \(v\) là vận tốc dài (m/s)
- \(R\) là bán kính của đường tròn (m)
- \(\omega\) là vận tốc góc (rad/s)
Ví dụ, nếu một chiếc xe đạp di chuyển với vận tốc 40 km/h (tương đương khoảng 11.1 m/s) trên một đường tròn có bán kính 100m, thì gia tốc hướng tâm có thể được tính như sau:
Như vậy, trong chuyển động tròn đều, cả vận tốc và gia tốc đóng vai trò quan trọng giúp xe di chuyển ổn định và an toàn trên đường cong.

4. Các bài toán thực tế liên quan đến chuyển động của xe đạp
Chuyển động của xe đạp không chỉ đơn giản là một hoạt động thể thao hoặc giải trí, mà còn chứa đựng nhiều bài toán thú vị liên quan đến vận tốc, gia tốc, và chuyển động trên các địa hình khác nhau. Dưới đây là một số ví dụ về các bài toán thực tế mà chúng ta có thể gặp trong quá trình tìm hiểu về chuyển động của xe đạp:
-
Bài toán 1: Tính thời gian để hoàn thành một vòng đua
- Cho một chiếc xe đạp chạy với vận tốc 40 km/h trên một đường đua có bán kính 100 m. Tính thời gian để xe đạp hoàn thành một vòng đua.
- Lời giải: Vận tốc tiếp tuyến \(v = 40 \, \text{km/h} = \frac{100}{9} \, \text{m/s}\). Chu vi của vòng đua là \(C = 2 \pi R = 2 \pi \times 100 = 200 \pi \, \text{m}\). Thời gian \(t\) để hoàn thành một vòng đua là: \[ t = \frac{C}{v} = \frac{200 \pi}{\frac{100}{9}} \approx 56.55 \, \text{s} \]
-
Bài toán 2: Tính quãng đường đi được khi giảm tốc độ
- Một chiếc xe đạp ban đầu chạy với vận tốc 40 km/h. Nếu giảm tốc độ đều đặn đến 20 km/h trong 10 giây, tính quãng đường đi được trong thời gian này.
- Lời giải: Gia tốc giảm tốc \(a = \frac{v_f - v_i}{t} = \frac{20 - 40}{10} = -2 \, \text{km/h/s}\). Đổi sang m/s\(^2\): \(a = -\frac{2 \times 1000}{3600} = -\frac{5}{9} \, \text{m/s}^2\). Quãng đường đi được trong thời gian giảm tốc là: \[ s = v_i t + \frac{1}{2} a t^2 = \left(\frac{100}{9} \times 10\right) + \frac{1}{2} \times \left(-\frac{5}{9}\right) \times 10^2 \approx 250 \, \text{m} \]
-
Bài toán 3: Tính vận tốc trung bình khi di chuyển trên đường dốc
- Một người đi xe đạp xuống dốc từ điểm A với vận tốc ban đầu 2 m/s và gia tốc 0,2 m/s\(^2\). Tính vận tốc trung bình sau 10 giây.
- Lời giải: Vận tốc cuối cùng \(v_f = v_i + at = 2 + 0,2 \times 10 = 4 \, \text{m/s}\). Vận tốc trung bình \(v_{\text{tb}} = \frac{v_i + v_f}{2} = \frac{2 + 4}{2} = 3 \, \text{m/s}\).
-
Bài toán 4: Tính khoảng cách giữa hai vật chuyển động tròn đều
- Một xe đạp và một ô tô bắt đầu di chuyển từ hai đầu của một đường dốc với các vận tốc khác nhau và gia tốc khác nhau. Xác định khoảng cách giữa chúng sau một khoảng thời gian nhất định.
- Lời giải: Để giải bài toán này, cần sử dụng các công thức chuyển động thẳng đều và chuyển động thẳng biến đổi đều, tính toán từng vị trí của xe đạp và ô tô tại mỗi thời điểm, sau đó tìm sự chênh lệch khoảng cách giữa hai vật.

5. Phân tích chuyên sâu về động lực học xe đạp
Động lực học của một chiếc xe đạp khi di chuyển với vận tốc 40 km/h liên quan chặt chẽ đến các yếu tố như gia tốc hướng tâm, lực ma sát, và sự cân bằng lực. Để hiểu rõ hơn về cách các yếu tố này tương tác và ảnh hưởng đến chuyển động của xe đạp, chúng ta sẽ phân tích từng khía cạnh dưới đây.
5.1. Ứng dụng định luật Newton trong chuyển động của xe đạp
Định luật II của Newton cho rằng gia tốc của một vật thể tỷ lệ thuận với lực tác dụng lên nó và tỷ lệ nghịch với khối lượng của vật thể đó, được biểu diễn bởi công thức:
\[ F = ma \]
Trong trường hợp của xe đạp, lực tác dụng chính là lực đẩy từ người đạp và lực cản từ không khí, mặt đường. Khi xe đạp chuyển động với vận tốc 40 km/h trên đường cong bán kính 100 m, gia tốc hướng tâm sẽ được tính bằng:
\[ a_{ht} = \frac{v^2}{r} = \frac{(40 \times \frac{1000}{3600})^2}{100} \approx 1.23 \, m/s^2 \]
Điều này cho thấy rằng xe đạp luôn cần một lực hướng tâm để giữ xe đi theo đường cong, lực này do ma sát giữa bánh xe và mặt đường cung cấp.
5.2. Cân bằng lực và ma sát trong chuyển động của xe đạp
Lực ma sát đóng vai trò quan trọng trong việc duy trì chuyển động ổn định của xe đạp. Khi xe đạp chuyển động trên bề mặt, lực ma sát giữa lốp xe và mặt đường sẽ chống lại lực cản từ không khí và lực hấp dẫn để xe không bị trượt. Lực ma sát tĩnh giữ cho xe không bị lệch khỏi quỹ đạo khi vào các khúc cua với tốc độ cao.
Công thức tính lực ma sát là:
\[ F_{ms} = \mu N \]
Trong đó, \(\mu\) là hệ số ma sát giữa bánh xe và mặt đường, \(N\) là lực phản lực từ mặt đường. Ở tốc độ 40 km/h, hệ số ma sát phải đủ lớn để cung cấp lực hướng tâm cần thiết để xe không bị trượt khỏi đường cong.
5.3. Động lực học và hiệu suất trong các cuộc đua xe đạp
Trong các cuộc đua xe đạp, hiệu suất là yếu tố quyết định, phụ thuộc vào việc tối ưu hóa các lực tác động. Người đạp xe phải điều chỉnh lực đạp và tư thế để giảm lực cản từ không khí, đồng thời tối ưu hóa lực ma sát để duy trì tốc độ cao mà không mất kiểm soát. Lực cản từ không khí có thể được giảm bớt bằng cách sử dụng tư thế khí động học, trong khi lực ma sát cần phải được cân bằng sao cho không quá lớn để cản trở tốc độ nhưng đủ để giữ vững hướng đi.
Ví dụ, trong một đường đua có nhiều khúc cua, người đạp cần giảm tốc độ trước khi vào cua để đảm bảo lực ma sát đủ lớn giữ xe trên quỹ đạo, sau đó tăng tốc ngay khi ra khỏi khúc cua để duy trì tốc độ trung bình cao.
Như vậy, việc hiểu rõ động lực học của xe đạp không chỉ giúp cải thiện hiệu suất trong các cuộc đua mà còn đảm bảo an toàn khi di chuyển ở tốc độ cao trên các đoạn đường phức tạp.
XEM THÊM:
6. Kết luận và những điều cần lưu ý khi tính toán chuyển động tròn
Qua quá trình nghiên cứu và phân tích động lực học của xe đạp di chuyển với vận tốc 40 km/h trên quãng đường cong, chúng ta rút ra một số kết luận quan trọng và những điều cần lưu ý khi tính toán chuyển động tròn.
6.1. Tổng kết về vận tốc, gia tốc và lực trong chuyển động tròn
Trong chuyển động tròn đều, vận tốc của xe đạp luôn thay đổi hướng nhưng có độ lớn không đổi. Gia tốc hướng tâm là một yếu tố quan trọng, nó luôn hướng về tâm của quỹ đạo và có độ lớn được tính bằng công thức:
\[
a_{\text{ht}} = \frac{v^2}{r}
\]
Với \(v\) là vận tốc tuyến tính của xe đạp và \(r\) là bán kính của quỹ đạo. Trong trường hợp xe đạp chạy với vận tốc 40 km/h (tương đương với 11.11 m/s) trên một quãng đường có bán kính 100 m, gia tốc hướng tâm được tính toán là:
\[
a_{\text{ht}} = \frac{(11.11)^2}{100} \approx 1.23 \, \text{m/s}^2
\]
Lực hướng tâm cần thiết để duy trì chuyển động tròn của xe đạp cũng có thể được tính dựa trên khối lượng xe và gia tốc hướng tâm.
6.2. Lưu ý về sự an toàn khi xe đạp di chuyển với vận tốc cao
Khi xe đạp di chuyển với vận tốc cao trên các quãng đường cong, lực hướng tâm đóng vai trò quan trọng trong việc giữ xe bám đường và duy trì quỹ đạo. Việc thiếu lực hướng tâm đủ lớn có thể dẫn đến tình trạng xe trượt khỏi đường đua. Do đó, cần đảm bảo rằng lực ma sát giữa lốp xe và mặt đường đủ lớn để cung cấp lực hướng tâm cần thiết.
6.3. Định hướng học tập và nghiên cứu thêm về vật lý chuyển động
Hiểu rõ về các khái niệm vật lý trong chuyển động tròn không chỉ giúp chúng ta dự đoán chính xác hành vi của các vật thể trong thực tế mà còn là cơ sở để áp dụng vào nhiều lĩnh vực khác như kỹ thuật, cơ khí, và thậm chí là thể thao. Các bài toán liên quan đến vận tốc, gia tốc và lực trong chuyển động tròn là nền tảng cho việc nghiên cứu và phát triển trong nhiều ngành khoa học và công nghệ.
Với những kiến thức này, chúng ta có thể tiếp tục khám phá và tìm hiểu sâu hơn về các hiện tượng vật lý, cũng như ứng dụng chúng vào thực tiễn cuộc sống.