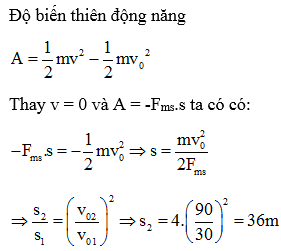Một xe điện đang chạy với vận tốc 36km/h: Phân tích và ứng dụng trong vật lý

Bài toán về chuyển động của một xe điện với vận tốc ban đầu \( v_0 = 36 \, \text{km/h} \) là một ví dụ điển hình trong các bài tập vật lý phổ thông. Dưới đây là các thông tin liên quan đến bài toán này:

1. Đổi đơn vị

Trước khi giải quyết bài toán, cần đổi đơn vị vận tốc từ km/h sang m/s:

2. Phân tích lực tác dụng

Xe điện khi hãm phanh đột ngột sẽ có các lực sau tác dụng:

• Trọng lực \( P = mg \)
• Lực của đường ray \( Q \)
• Lực ma sát trượt \( F_{\text{mst}} = \mu_t \cdot N = \mu_t \cdot mg \)

Theo định luật II Newton:

3. Tính toán gia tốc

Gia tốc của xe điện khi bị hãm phanh được tính như sau:

Với hệ số ma sát trượt \( \mu_t = 0.2 \) và gia tốc trọng trường \( g = 9.8 \, \text{m/s}^2 \), ta có:

4. Tính quãng đường xe đi thêm

Quãng đường mà xe điện đi được sau khi hãm phanh đến khi dừng lại hoàn toàn được tính theo công thức:

Thay các giá trị vào công thức, ta có:

Như vậy, quãng đường xe điện đi được sau khi hãm phanh là 25.51 mét.

5. Các bài toán tương tự

Đây là một bài toán cơ bản về động lực học, thường gặp trong các đề thi vật lý trung học phổ thông. Các bài toán tương tự có thể yêu cầu tính lực ma sát, quãng đường, hay thời gian dừng lại của xe trong các điều kiện khác nhau.

Bài toán về "một xe điện đang chạy với vận tốc 36km/h" là một bài tập cơ bản trong chương trình vật lý phổ thông, thường được sử dụng để giảng dạy về các khái niệm cơ bản của động lực học. Bài toán này giúp học sinh hiểu rõ hơn về chuyển động thẳng đều, lực tác dụng, gia tốc, và các khái niệm liên quan khác.

Trong bài toán này, xe điện được coi là một vật chuyển động với vận tốc không đổi ban đầu là \(v_0 = 36 \, \text{km/h}\). Khi lực hãm phanh được áp dụng, xe điện sẽ bắt đầu giảm tốc độ. Nhiệm vụ của học sinh là tính toán các yếu tố như lực ma sát, gia tốc, quãng đường đi thêm, và thời gian cần để xe điện dừng hẳn.

Để dễ hiểu hơn, chúng ta có thể chuyển đổi vận tốc từ km/h sang m/s:

Với vận tốc này, bài toán sẽ yêu cầu các bước tính toán tiếp theo để xác định gia tốc của xe khi hãm phanh, lực ma sát giữa bánh xe và mặt đường ray, và các đại lượng vật lý khác liên quan.

Bài toán này không chỉ mang tính lý thuyết mà còn có ứng dụng thực tiễn trong việc phân tích các tình huống tương tự trong đời sống, chẳng hạn như khi một phương tiện giao thông đột ngột phanh lại. Điều này giúp học sinh nắm bắt rõ hơn về cách các nguyên lý vật lý được áp dụng trong thực tế.

Để giải bài toán "một xe điện đang chạy với vận tốc 36km/h", chúng ta cần thực hiện các bước sau:

1. Bước 1: Đổi đơn vị vận tốc

   Trước hết, chúng ta cần chuyển đổi vận tốc từ km/h sang m/s để thuận tiện cho việc tính toán:

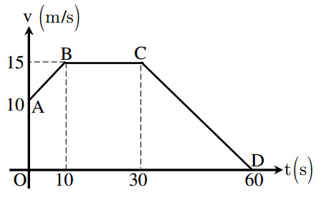
   \[ v_0 = 36 \, \text{km/h} = \frac{36 \times 1000}{3600} = 10 \, \text{m/s} \]

2. Bước 2: Xác định các lực tác dụng lên xe

   Xe điện chịu tác động của các lực chính như sau:

   • Trọng lực \( P = mg \)
   • Lực ma sát trượt \( F_{\text{mst}} = \mu_t \cdot N \), trong đó \( \mu_t \) là hệ số ma sát trượt và \( N \) là phản lực từ mặt đường.
   • Lực hãm phanh \( F_{\text{h}} \)

   Các lực này sẽ quyết định gia tốc của xe khi phanh.

3. Bước 3: Tính gia tốc của xe khi hãm phanh

   Gia tốc của xe có thể được tính dựa trên định luật II Newton:

   \[ F_{\text{mst}} = ma = \mu_t \cdot mg \]

   Do đó, gia tốc của xe là:

   \[ a = \mu_t \cdot g \]

   Với \( g = 9.8 \, \text{m/s}^2 \) và \( \mu_t \) là hệ số ma sát trượt.

4. Bước 4: Tính quãng đường xe đi được sau khi phanh

   Quãng đường xe điện đi được cho đến khi dừng hẳn có thể được tính bằng phương trình chuyển động:

   \[ v^2 - v_0^2 = 2as \]

   Thay các giá trị vào công thức để tính \( s \), trong đó \( v = 0 \) khi xe dừng lại:

   \[ 0 - 10^2 = 2 \times (-a) \times s \] \[ s = \frac{100}{2a} \]

5. Bước 5: Tính thời gian xe dừng lại hoàn toàn

   Thời gian để xe dừng lại có thể được tính từ công thức:

   \[ t = \frac{v_0 - v}{a} \]

   Thay \( v = 0 \) khi xe dừng lại và sử dụng giá trị của \( a \) từ bước 3.

Bài toán về "một xe điện đang chạy với vận tốc 36km/h" không chỉ mang tính thực tiễn cao mà còn là công cụ giáo dục quan trọng. Bài toán giúp học sinh hiểu rõ hơn về các khái niệm như vận tốc, ma sát, và động lực học thông qua các tình huống thực tế. Đây là cơ hội để phát triển tư duy logic, kỹ năng giải quyết vấn đề, và ứng dụng các nguyên lý vật lý trong cuộc sống hàng ngày. Ngoài ra, bài toán này cũng là nền tảng cho các bài học về an toàn giao thông và hiệu quả năng lượng.

Bài toán về "một xe điện đang chạy với vận tốc 36km/h" là một ví dụ điển hình giúp học sinh nắm vững các khái niệm cơ bản trong động lực học. Thông qua việc giải quyết các bước từ đổi đơn vị, xác định lực tác dụng, tính gia tốc đến tính toán quãng đường và thời gian, học sinh không chỉ rèn luyện kỹ năng tính toán mà còn hiểu rõ hơn về ứng dụng của các nguyên lý vật lý trong thực tế.

Hơn nữa, bài toán này còn mang lại ý nghĩa giáo dục sâu sắc khi liên hệ trực tiếp với các tình huống trong đời sống, như phân tích quá trình hãm phanh của phương tiện giao thông. Việc vận dụng các kiến thức đã học để giải quyết bài toán này không chỉ củng cố hiểu biết mà còn giúp học sinh phát triển tư duy logic và khả năng giải quyết vấn đề một cách sáng tạo và hiệu quả.

Nhìn chung, bài toán "một xe điện đang chạy với vận tốc 36km/h" không chỉ là một bài tập lý thuyết mà còn là công cụ giảng dạy mạnh mẽ, đóng góp vào việc phát triển toàn diện các kỹ năng học tập và hiểu biết thực tiễn cho học sinh.