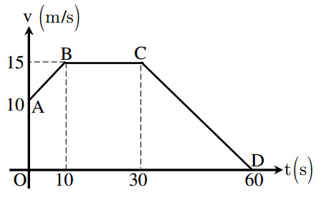
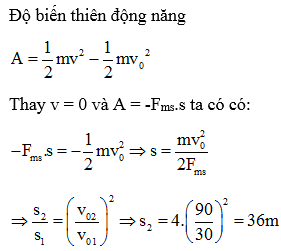Chủ đề vận tốc xuôi dòng và ngược dòng: Khám phá cách tính toán vận tốc xuôi dòng và ngược dòng một cách chính xác và hiệu quả. Bài viết này sẽ giúp bạn nắm vững các công thức cơ bản, đồng thời cung cấp những ví dụ thực tế và ứng dụng trong đời sống để giúp bạn tự tin áp dụng vào các tình huống khác nhau.
Mục lục
Vận Tốc Xuôi Dòng và Ngược Dòng
Vận tốc xuôi dòng và ngược dòng là một khái niệm quan trọng trong các bài toán chuyển động liên quan đến dòng nước. Để hiểu rõ hơn về cách tính toán và ứng dụng, dưới đây là các thông tin chi tiết:
1. Khái Niệm
- Vận tốc xuôi dòng: Là vận tốc của một vật chuyển động cùng chiều với dòng nước. Trong trường hợp này, vận tốc của vật sẽ được cộng thêm với vận tốc của dòng nước.
- Vận tốc ngược dòng: Là vận tốc của một vật chuyển động ngược chiều với dòng nước. Khi đó, vận tốc của dòng nước sẽ trừ đi từ vận tốc của vật.
2. Công Thức Tính
Công thức tính vận tốc xuôi dòng và ngược dòng có thể được mô tả như sau:
\[
v_{xuôi} = v_{vật} + v_{nước}
\]
\[
v_{ngược} = v_{vật} - v_{nước}
\]
3. Ví Dụ Minh Họa
Giả sử một chiếc thuyền có vận tốc trong nước tĩnh là \( v_{thuyền} \) = 10 km/h. Dòng nước chảy với vận tốc \( v_{nước} \) = 2 km/h.
\[
v_{xuôi} = 10 + 2 = 12 \text{ km/h}
\]
\[
v_{ngược} = 10 - 2 = 8 \text{ km/h}
\]
4. Ứng Dụng Thực Tiễn
Hiểu rõ về vận tốc xuôi dòng và ngược dòng giúp ích rất nhiều trong các tình huống thực tế như điều khiển thuyền, máy bay, hoặc tính toán thời gian di chuyển của một phương tiện trên sông hoặc biển. Đây là những yếu tố quan trọng giúp đưa ra quyết định hợp lý trong việc lập kế hoạch di chuyển hoặc thực hiện các chiến lược tối ưu hóa trong giao thông vận tải.

.png)
1. Khái Niệm Vận Tốc Xuôi Dòng và Ngược Dòng
Trong vật lý, vận tốc xuôi dòng và ngược dòng là hai khái niệm cơ bản liên quan đến chuyển động của một vật thể trong môi trường chất lỏng, chẳng hạn như sông hoặc biển. Đây là các khái niệm quan trọng khi nghiên cứu các bài toán liên quan đến chuyển động trên dòng nước.
Vận tốc xuôi dòng là vận tốc của một vật thể khi nó di chuyển cùng chiều với dòng nước. Vận tốc này được xác định bằng cách cộng vận tốc của dòng nước vào vận tốc của vật thể khi nó di chuyển trong môi trường nước tĩnh.
Công thức tính vận tốc xuôi dòng được mô tả như sau:
\[
v_{xuôi} = v_{vật} + v_{nước}
\]
Vận tốc ngược dòng là vận tốc của một vật thể khi nó di chuyển ngược chiều với dòng nước. Trong trường hợp này, vận tốc của vật thể sẽ bị giảm đi do phải chống lại lực đẩy của dòng nước.
Công thức tính vận tốc ngược dòng được biểu diễn bằng công thức:
\[
v_{ngược} = v_{vật} - v_{nước}
\]
Trong đó:
- \( v_{vật} \) là vận tốc của vật thể trong nước tĩnh.
- \( v_{nước} \) là vận tốc của dòng nước.
- \( v_{xuôi} \) là vận tốc xuôi dòng.
- \( v_{ngược} \) là vận tốc ngược dòng.
Những khái niệm này không chỉ có ý nghĩa trong lý thuyết mà còn được áp dụng rộng rãi trong các lĩnh vực như hàng hải, vận tải, và thể thao dưới nước, nơi việc tính toán chính xác vận tốc là cần thiết để đảm bảo an toàn và hiệu quả trong quá trình di chuyển.
2. Công Thức Tính Vận Tốc Xuôi Dòng và Ngược Dòng
Trong các bài toán chuyển động trên dòng nước, việc tính toán vận tốc xuôi dòng và ngược dòng là rất quan trọng. Các công thức này giúp xác định vận tốc thực tế của một vật thể khi di chuyển trong dòng nước, từ đó đưa ra các quyết định phù hợp trong quá trình di chuyển. Dưới đây là các công thức chi tiết:
2.1. Công Thức Tính Vận Tốc Xuôi Dòng
Vận tốc xuôi dòng là vận tốc của vật thể khi nó di chuyển cùng chiều với dòng nước. Công thức tính vận tốc xuôi dòng được xác định như sau:
\[
v_{xuôi} = v_{vật} + v_{nước}
\]
Trong đó:
- \( v_{xuôi} \): Vận tốc xuôi dòng.
- \( v_{vật} \): Vận tốc của vật thể khi di chuyển trong nước tĩnh.
- \( v_{nước} \): Vận tốc của dòng nước.
2.2. Công Thức Tính Vận Tốc Ngược Dòng
Vận tốc ngược dòng là vận tốc của vật thể khi nó di chuyển ngược chiều với dòng nước. Công thức tính vận tốc ngược dòng được biểu diễn như sau:
\[
v_{ngược} = v_{vật} - v_{nước}
\]
Trong đó:
- \( v_{ngược} \): Vận tốc ngược dòng.
- \( v_{vật} \): Vận tốc của vật thể khi di chuyển trong nước tĩnh.
- \( v_{nước} \): Vận tốc của dòng nước.
2.3. Lưu Ý Khi Áp Dụng Công Thức
Để áp dụng chính xác các công thức trên, cần lưu ý những điểm sau:
- Cần xác định đúng vận tốc của vật thể trong nước tĩnh \( v_{vật} \) và vận tốc của dòng nước \( v_{nước} \) trước khi áp dụng công thức.
- Vận tốc xuôi dòng luôn lớn hơn vận tốc trong nước tĩnh, trong khi vận tốc ngược dòng luôn nhỏ hơn.
- Tránh nhầm lẫn giữa vận tốc xuôi dòng và ngược dòng trong quá trình tính toán, vì điều này có thể dẫn đến sai lệch kết quả.

3. Ví Dụ Minh Họa Về Vận Tốc Xuôi Dòng và Ngược Dòng
Để hiểu rõ hơn về cách tính vận tốc xuôi dòng và ngược dòng, hãy cùng xem qua một số ví dụ minh họa cụ thể dưới đây. Các ví dụ này sẽ giúp bạn hình dung rõ ràng hơn về cách áp dụng các công thức đã học vào thực tế.
3.1. Ví Dụ 1: Tính Vận Tốc Xuôi Dòng
Giả sử một chiếc thuyền di chuyển trên dòng sông có vận tốc trong nước tĩnh là \( v_{thuyền} = 10 \, \text{km/h} \). Vận tốc của dòng nước là \( v_{nước} = 2 \, \text{km/h} \). Hãy tính vận tốc xuôi dòng của thuyền.
Theo công thức tính vận tốc xuôi dòng:
\[
v_{xuôi} = v_{thuyền} + v_{nước}
\]
Thay các giá trị vào công thức:
\[
v_{xuôi} = 10 \, \text{km/h} + 2 \, \text{km/h} = 12 \, \text{km/h}
\]
Vậy vận tốc xuôi dòng của thuyền là \( 12 \, \text{km/h} \).
3.2. Ví Dụ 2: Tính Vận Tốc Ngược Dòng
Tiếp tục với chiếc thuyền trên, nếu nó di chuyển ngược dòng, tức là ngược chiều với dòng nước, hãy tính vận tốc ngược dòng.
Theo công thức tính vận tốc ngược dòng:
\[
v_{ngược} = v_{thuyền} - v_{nước}
\]
Thay các giá trị vào công thức:
\[
v_{ngược} = 10 \, \text{km/h} - 2 \, \text{km/h} = 8 \, \text{km/h}
\]
Vậy vận tốc ngược dòng của thuyền là \( 8 \, \text{km/h} \).
3.3. Ví Dụ 3: Tính Thời Gian Di Chuyển
Giả sử thuyền cần di chuyển một quãng đường dài 24 km. Tính thời gian cần thiết để thuyền đi hết quãng đường này khi:
- Xuôi dòng: \( v_{xuôi} = 12 \, \text{km/h} \)
- Ngược dòng: \( v_{ngược} = 8 \, \text{km/h} \)
Thời gian xuôi dòng:
\[
t_{xuôi} = \frac{s}{v_{xuôi}} = \frac{24 \, \text{km}}{12 \, \text{km/h}} = 2 \, \text{giờ}
\]
Thời gian ngược dòng:
\[
t_{ngược} = \frac{s}{v_{ngược}} = \frac{24 \, \text{km}}{8 \, \text{km/h}} = 3 \, \text{giờ}
\]
Vậy, thuyền sẽ mất 2 giờ để di chuyển xuôi dòng và 3 giờ để di chuyển ngược dòng trên quãng đường 24 km.

4. Ứng Dụng Thực Tiễn Của Vận Tốc Xuôi Dòng và Ngược Dòng
Vận tốc xuôi dòng và ngược dòng không chỉ là các khái niệm lý thuyết mà còn có nhiều ứng dụng thực tiễn trong đời sống hàng ngày, giao thông vận tải, và các lĩnh vực khoa học kỹ thuật. Dưới đây là một số ứng dụng cụ thể của các khái niệm này.
4.1. Ứng Dụng Trong Hàng Hải
Trong hàng hải, việc hiểu và tính toán chính xác vận tốc xuôi dòng và ngược dòng là vô cùng quan trọng. Các thuyền trưởng cần phải biết vận tốc thực tế của tàu khi di chuyển trên biển để điều chỉnh lộ trình sao cho tiết kiệm nhiên liệu và thời gian.
Ví dụ, khi tàu đi xuôi dòng, thuyền trưởng có thể tận dụng dòng chảy để giảm thời gian di chuyển. Ngược lại, khi đi ngược dòng, cần phải dự đoán chính xác thời gian và lượng nhiên liệu cần thiết để đảm bảo hành trình an toàn.
4.2. Ứng Dụng Trong Giao Thông Vận Tải
Trong các hệ thống giao thông đường thủy như phà hoặc tàu chở hàng, vận tốc xuôi dòng và ngược dòng ảnh hưởng trực tiếp đến thời gian vận chuyển và hiệu quả kinh tế. Các nhà quản lý cần tính toán kỹ lưỡng để tối ưu hóa lộ trình, đặc biệt khi đối mặt với các điều kiện thời tiết bất lợi.
4.3. Ứng Dụng Trong Thể Thao Dưới Nước
Trong các môn thể thao dưới nước như bơi lội, chèo thuyền, vận tốc xuôi dòng và ngược dòng đóng vai trò quan trọng trong việc lập kế hoạch chiến thuật. Vận động viên cần tính toán kỹ lưỡng để tận dụng tối đa lợi thế từ dòng nước hoặc điều chỉnh chiến thuật khi phải bơi ngược dòng.
4.4. Ứng Dụng Trong Khoa Học và Nghiên Cứu
Các nhà khoa học và nhà nghiên cứu thường sử dụng các khái niệm về vận tốc xuôi dòng và ngược dòng trong nghiên cứu về dòng chảy, ô nhiễm nước, và các mô hình dự báo thời tiết. Những kiến thức này giúp họ hiểu rõ hơn về cách mà các yếu tố tự nhiên tương tác với nhau và ảnh hưởng đến môi trường xung quanh.
Như vậy, vận tốc xuôi dòng và ngược dòng có nhiều ứng dụng thực tiễn quan trọng, không chỉ trong các ngành công nghiệp mà còn trong nhiều lĩnh vực của đời sống và khoa học. Việc nắm vững các khái niệm này sẽ giúp chúng ta đưa ra các quyết định chính xác và hiệu quả hơn trong nhiều tình huống khác nhau.

5. Bài Tập Thực Hành Về Vận Tốc Xuôi Dòng và Ngược Dòng
Để củng cố kiến thức về vận tốc xuôi dòng và ngược dòng, dưới đây là một số bài tập thực hành giúp bạn áp dụng các công thức và khái niệm đã học vào các tình huống cụ thể. Hãy làm từng bài tập một cách cẩn thận và kiểm tra lại kết quả để đảm bảo hiểu đúng vấn đề.
5.1. Bài Tập 1: Tính Vận Tốc Xuôi Dòng
Một chiếc thuyền có vận tốc trong nước tĩnh là \( v_{thuyền} = 15 \, \text{km/h} \). Vận tốc của dòng nước là \( v_{nước} = 3 \, \text{km/h} \). Hãy tính vận tốc xuôi dòng của thuyền khi nó di chuyển cùng chiều với dòng nước.
Gợi ý: Áp dụng công thức:
\[
v_{xuôi} = v_{thuyền} + v_{nước}
\]
5.2. Bài Tập 2: Tính Vận Tốc Ngược Dòng
Tiếp tục với chiếc thuyền ở bài tập 1, hãy tính vận tốc ngược dòng của thuyền khi nó di chuyển ngược chiều với dòng nước.
Gợi ý: Áp dụng công thức:
\[
v_{ngược} = v_{thuyền} - v_{nước}
\]
5.3. Bài Tập 3: Tính Thời Gian Di Chuyển
Một chiếc ca-nô di chuyển với vận tốc trong nước tĩnh là \( v_{ca-nô} = 20 \, \text{km/h} \). Vận tốc của dòng nước là \( v_{nước} = 4 \, \text{km/h} \). Chiếc ca-nô cần đi một quãng đường dài 40 km.
- Câu hỏi 1: Tính thời gian cần thiết để ca-nô đi hết quãng đường này khi di chuyển xuôi dòng.
- Câu hỏi 2: Tính thời gian cần thiết để ca-nô đi hết quãng đường này khi di chuyển ngược dòng.
Gợi ý:
- Thời gian xuôi dòng: \[ t_{xuôi} = \frac{s}{v_{xuôi}} = \frac{40 \, \text{km}}{v_{ca-nô} + v_{nước}} \]
- Thời gian ngược dòng: \[ t_{ngược} = \frac{s}{v_{ngược}} = \frac{40 \, \text{km}}{v_{ca-nô} - v_{nước}} \]
5.4. Bài Tập 4: Xác Định Vận Tốc Dòng Nước
Một người bơi có vận tốc trong nước tĩnh là \( v_{bơi} = 5 \, \text{km/h} \). Khi bơi xuôi dòng, người này mất 1 giờ để đi hết quãng đường 7 km. Hãy tính vận tốc của dòng nước.
Gợi ý: Sử dụng phương trình:
\[
v_{xuôi} = v_{bơi} + v_{nước}
\]
Và từ đó tìm ra \( v_{nước} \).
Những bài tập trên giúp bạn thực hành tính toán vận tốc xuôi dòng và ngược dòng trong các tình huống khác nhau. Hãy chắc chắn rằng bạn đã hiểu rõ cách áp dụng công thức và xử lý các biến số trước khi tiến hành giải bài tập.
XEM THÊM:
6. Kết Luận
Vận tốc xuôi dòng và ngược dòng không chỉ là những khái niệm cơ bản trong vật lý mà còn có ý nghĩa quan trọng trong nhiều lĩnh vực đời sống và kỹ thuật. Hiểu rõ và áp dụng chính xác các công thức tính toán vận tốc xuôi dòng và ngược dòng giúp chúng ta giải quyết hiệu quả các bài toán liên quan đến chuyển động trong nước, đồng thời cũng mở ra nhiều ứng dụng thực tiễn hữu ích.
Việc nắm vững khái niệm này giúp tăng cường khả năng phân tích và giải quyết vấn đề, đặc biệt là trong các tình huống đòi hỏi sự tính toán chính xác như trong giao thông vận tải hoặc kỹ thuật. Bên cạnh đó, vận tốc xuôi dòng và ngược dòng còn được áp dụng rộng rãi trong đời sống hàng ngày, giúp tối ưu hóa thời gian và chi phí trong việc di chuyển và vận tải.
Cuối cùng, để nâng cao kiến thức và khả năng ứng dụng của mình, người học nên thường xuyên thực hành thông qua các bài tập từ cơ bản đến nâng cao. Đồng thời, tự nghiên cứu và cập nhật thêm những kiến thức mới sẽ giúp hiểu sâu hơn về các khái niệm này và áp dụng chúng một cách linh hoạt trong nhiều tình huống khác nhau.
6.1 Tầm Quan Trọng Của Việc Hiểu Vận Tốc Xuôi Dòng và Ngược Dòng
Việc hiểu rõ vận tốc xuôi dòng và ngược dòng là nền tảng giúp người học giải quyết các bài toán chuyển động trong môi trường nước một cách hiệu quả. Điều này không chỉ giúp tăng cường khả năng tư duy logic mà còn giúp áp dụng kiến thức vào thực tế một cách linh hoạt và sáng tạo.
6.2 Hướng Dẫn Tự Học Và Nâng Cao Kiến Thức
Để tự học và nâng cao kiến thức về vận tốc xuôi dòng và ngược dòng, người học có thể áp dụng các bước sau:
- Thường xuyên ôn tập các khái niệm cơ bản và công thức liên quan.
- Làm bài tập từ cơ bản đến nâng cao để củng cố kiến thức.
- Nghiên cứu thêm các tài liệu nâng cao và ứng dụng thực tiễn của vận tốc xuôi dòng và ngược dòng.
- Tham gia các diễn đàn học thuật để trao đổi kiến thức và kinh nghiệm.
Việc kiên trì học tập và thực hành sẽ giúp người học nắm vững kiến thức và có thể áp dụng một cách hiệu quả trong thực tế.