Lực Hướng Tâm: Khám Phá Khái Niệm, Ứng Dụng và Tác Động Trong Đời Sống

Lực hướng tâm là một khái niệm cơ bản trong vật lý học, đặc biệt trong lĩnh vực cơ học. Lực này có vai trò giữ cho một vật thể chuyển động tròn đều quanh một tâm quay, và nó luôn hướng về phía tâm của quỹ đạo.

Định nghĩa và Công Thức

Lực hướng tâm là lực tác động lên một vật khi vật đó chuyển động tròn đều quanh một trục hoặc tâm quay. Lực này có thể được định nghĩa thông qua công thức sau:

$$F_{ht} = \dfrac{m \cdot v^2}{r}$$

Trong đó:

• \(F_{ht}\): Lực hướng tâm (Newton)
• \(m\): Khối lượng của vật thể (kg)
• \(v\): Vận tốc của vật thể (m/s)
• \(r\): Bán kính của quỹ đạo tròn (m)

Vai Trò Của Lực Hướng Tâm

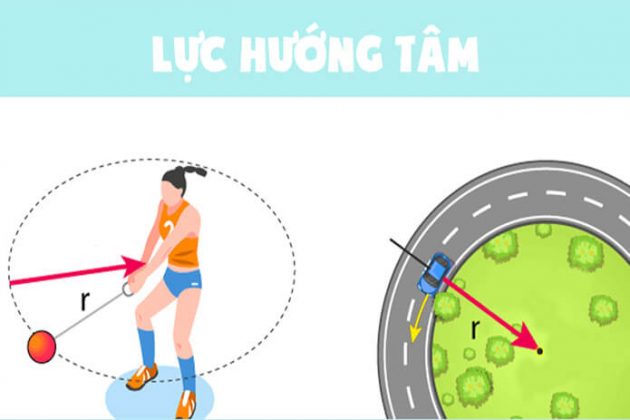
Lực hướng tâm giữ cho một vật thể chuyển động theo một đường tròn, ngăn không cho vật bay ra khỏi quỹ đạo. Lực này có thể là kết quả của nhiều lực khác nhau tùy thuộc vào bối cảnh, chẳng hạn như:

• Lực hấp dẫn: Đối với các hành tinh quay quanh mặt trời.
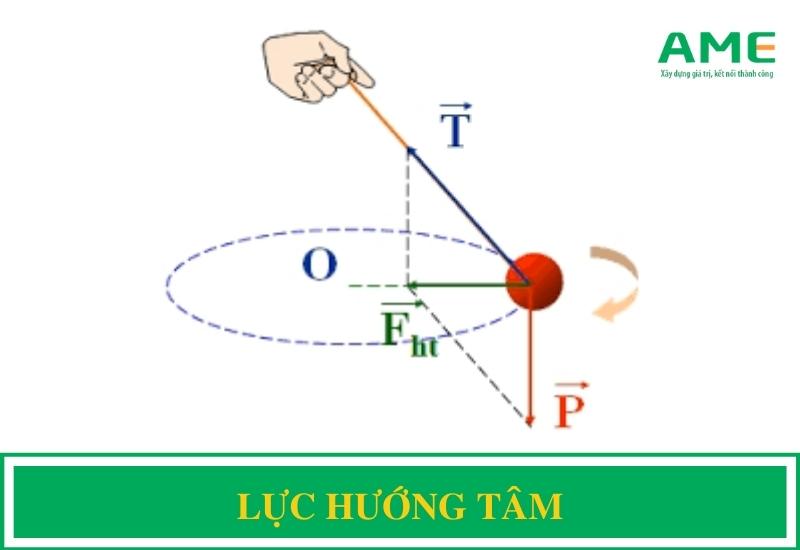
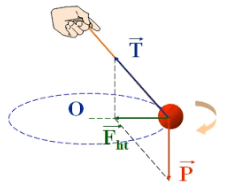
• Lực căng dây: Đối với vật quay trên một dây treo.
• Lực ma sát: Đối với xe cộ khi quay vòng trên đường.

Ứng Dụng Của Lực Hướng Tâm

Lực hướng tâm có nhiều ứng dụng trong đời sống và kỹ thuật, bao gồm:

1. Thiết kế đường cong trong giao thông: Để đảm bảo an toàn, đường cong được thiết kế với bán kính phù hợp để tạo ra lực hướng tâm cần thiết giúp phương tiện không bị văng ra ngoài.
2. Quay li tâm: Trong các máy quay li tâm, lực hướng tâm được tận dụng để tách các thành phần khác nhau trong một hỗn hợp.
3. Vòng quay: Trong các trò chơi giải trí như vòng quay, lực hướng tâm giữ cho các ghế ngồi hoặc vật thể quay quanh trục mà không bị rơi.

Tính Chất Của Lực Hướng Tâm

Một số tính chất đáng chú ý của lực hướng tâm bao gồm:

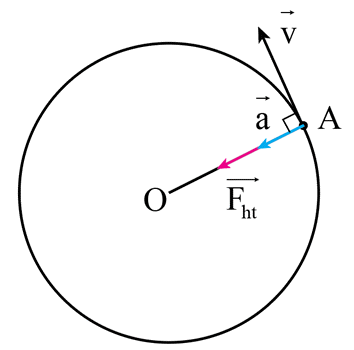
• Lực hướng tâm không sinh công, vì nó vuông góc với phương chuyển động của vật thể.
• Lực hướng tâm luôn hướng về phía tâm của đường tròn hoặc quỹ đạo cong.
• Độ lớn của lực hướng tâm phụ thuộc vào khối lượng, vận tốc của vật và bán kính của quỹ đạo.

Lực hướng tâm là một lực quan trọng trong cơ học, đặc biệt là trong các hiện tượng liên quan đến chuyển động tròn. Đây là lực tác động lên một vật thể để duy trì chuyển động của nó theo một quỹ đạo cong hoặc tròn, và luôn hướng về tâm của quỹ đạo đó.

Để hiểu rõ hơn về lực hướng tâm, ta có thể xem xét các khía cạnh sau:

• Định nghĩa: Lực hướng tâm là lực cần thiết để duy trì một vật thể trong chuyển động tròn đều. Lực này luôn hướng vào phía tâm của đường tròn mà vật thể đang chuyển động trên đó.
• Công thức tính toán: Công thức tính lực hướng tâm được biểu diễn như sau:

  
  $$F_{ht} = \dfrac{m \cdot v^2}{r}$$

  Trong đó:

  • \(F_{ht}\): Lực hướng tâm (Newton)
  • \(m\): Khối lượng của vật thể (kg)
  • \(v\): Vận tốc của vật thể (m/s)
  • \(r\): Bán kính của quỹ đạo tròn (m)
• Vai trò của lực hướng tâm: Lực hướng tâm giữ cho vật thể không bị bay ra khỏi quỹ đạo khi chuyển động tròn. Đây là lực ngăn chặn sự chuyển động theo phương tiếp tuyến mà nếu không có nó, vật thể sẽ di chuyển thẳng ra khỏi quỹ đạo theo định luật quán tính.
• Các nguồn gốc của lực hướng tâm: Lực hướng tâm có thể xuất phát từ nhiều loại lực khác nhau trong tự nhiên, bao gồm lực hấp dẫn, lực ma sát, lực căng dây, và các lực khác phụ thuộc vào ngữ cảnh cụ thể của vấn đề.

Hiểu biết về lực hướng tâm giúp giải thích nhiều hiện tượng tự nhiên và ứng dụng trong đời sống hàng ngày, từ chuyển động của các hành tinh xung quanh mặt trời đến các trò chơi giải trí và công nghệ hiện đại.

Lực hướng tâm, vốn giữ cho một vật thể di chuyển theo quỹ đạo tròn, phụ thuộc vào nhiều yếu tố khác nhau. Các yếu tố này ảnh hưởng trực tiếp đến độ lớn của lực hướng tâm cần thiết để duy trì chuyển động tròn đều của vật thể. Dưới đây là những yếu tố chính ảnh hưởng đến lực hướng tâm:

• Khối lượng của vật thể (\(m\)):

  Khối lượng của vật thể là yếu tố đầu tiên ảnh hưởng đến lực hướng tâm. Theo công thức tính toán lực hướng tâm:

  
  $$F_{ht} = \dfrac{m \cdot v^2}{r}$$

  Ta thấy rằng lực hướng tâm tỉ lệ thuận với khối lượng của vật thể. Điều này có nghĩa là khi khối lượng tăng, lực hướng tâm cần thiết để giữ vật trong quỹ đạo cũng tăng lên.

• Vận tốc của vật thể (\(v\)):

  Vận tốc là một yếu tố quan trọng khác. Lực hướng tâm tỉ lệ thuận với bình phương của vận tốc, tức là:

  
  $$F_{ht} \propto v^2$$

  Điều này có nghĩa là khi vận tốc của vật thể tăng gấp đôi, lực hướng tâm cần thiết sẽ tăng lên gấp bốn lần. Vận tốc càng cao, lực hướng tâm càng lớn để giữ cho vật thể không bị văng ra khỏi quỹ đạo tròn.

• Bán kính của quỹ đạo (\(r\)):

  Bán kính của quỹ đạo là yếu tố thứ ba ảnh hưởng đến lực hướng tâm. Theo công thức, lực hướng tâm tỉ lệ nghịch với bán kính của quỹ đạo:

  
  $$F_{ht} = \dfrac{m \cdot v^2}{r}$$

  Nghĩa là, khi bán kính của quỹ đạo tăng lên, lực hướng tâm cần thiết sẽ giảm xuống. Ngược lại, với quỹ đạo nhỏ hơn, lực hướng tâm sẽ phải lớn hơn để giữ vật thể trong chuyển động tròn.

• Lực tác dụng từ bên ngoài:

  Các lực từ bên ngoài như lực ma sát, lực hấp dẫn, hay lực căng dây cũng ảnh hưởng đến lực hướng tâm. Ví dụ, lực ma sát giữa bánh xe và mặt đường đóng vai trò là lực hướng tâm giữ cho xe di chuyển trên quỹ đạo cong mà không trượt ra ngoài.

Như vậy, hiểu rõ các yếu tố này giúp ta tính toán và dự đoán chính xác lực hướng tâm cần thiết trong các ứng dụng thực tiễn, từ thiết kế đường cong cho xe cộ đến việc điều chỉnh tốc độ của các vật thể quay trong máy móc công nghiệp.

Lực hướng tâm không chỉ là một khái niệm lý thuyết mà còn có rất nhiều ứng dụng thực tiễn trong đời sống và công nghệ. Dưới đây là một số ứng dụng nổi bật của lực hướng tâm mà chúng ta có thể gặp trong nhiều lĩnh vực khác nhau:

• Giao thông vận tải:

  Trong thiết kế đường cong cho phương tiện giao thông như ô tô và xe máy, lực hướng tâm đóng vai trò quan trọng. Để các phương tiện có thể di chuyển an toàn trên đường cong mà không bị trượt ra ngoài, lực hướng tâm phải đủ lớn để cân bằng với lực quán tính của phương tiện. Điều này đòi hỏi việc thiết kế bán kính đường cong, góc nghiêng của đường và tốc độ giới hạn phù hợp.

• Thiết bị quay li tâm:

  Các máy quay li tâm sử dụng lực hướng tâm để phân tách các thành phần khác nhau trong một hỗn hợp. Ví dụ, trong y học, máy quay li tâm được sử dụng để tách các tế bào máu khỏi huyết tương. Các phần tử nặng hơn sẽ di chuyển ra ngoài theo hướng của lực hướng tâm, trong khi các phần tử nhẹ hơn sẽ nằm gần tâm quay hơn.

• Trò chơi giải trí:

  Trong các trò chơi như vòng quay ngựa gỗ hay tàu lượn siêu tốc, lực hướng tâm là yếu tố tạo nên cảm giác hồi hộp và thú vị cho người chơi. Khi vòng quay tăng tốc, lực hướng tâm giữ người chơi ở vị trí cố định trên ghế ngồi mà không bị văng ra ngoài, tạo cảm giác ly kỳ và an toàn.

• Vận hành vệ tinh và tàu vũ trụ:

  Trong không gian, lực hấp dẫn của Trái Đất đóng vai trò như lực hướng tâm, giữ cho các vệ tinh và tàu vũ trụ quay quanh quỹ đạo mà không bị trôi ra ngoài không gian. Tính toán chính xác lực này là cần thiết để đưa vệ tinh vào quỹ đạo mong muốn và duy trì nó ở vị trí ổn định.

Những ứng dụng này minh họa vai trò quan trọng của lực hướng tâm trong việc duy trì chuyển động tròn và đảm bảo an toàn, hiệu quả trong nhiều lĩnh vực khác nhau của cuộc sống và khoa học kỹ thuật.

Lực hướng tâm, với vai trò duy trì chuyển động tròn của vật thể, mang nhiều tính chất đặc biệt quan trọng trong việc hiểu và áp dụng trong các hiện tượng vật lý. Dưới đây là một số tính chất nổi bật của lực hướng tâm:

• Lực hướng tâm không sinh công:

  Mặc dù lực hướng tâm duy trì chuyển động của một vật thể trong quỹ đạo tròn, nó không sinh công. Điều này là do lực hướng tâm luôn vuông góc với vận tốc tức thời của vật thể, tức là nó không làm thay đổi độ lớn của vận tốc mà chỉ thay đổi hướng của vận tốc. Công suất sinh ra bởi lực hướng tâm do đó bằng không.

• Lực hướng tâm luôn hướng về tâm của quỹ đạo:

  Một trong những tính chất đặc trưng của lực hướng tâm là nó luôn hướng vào phía tâm của đường tròn mà vật thể chuyển động. Điều này có nghĩa là bất kể vị trí của vật thể trên quỹ đạo, lực hướng tâm sẽ luôn kéo vật thể về phía trung tâm, giữ cho vật thể không bị văng ra khỏi quỹ đạo.

• Lực hướng tâm không phải là một lực mới:

  Lực hướng tâm thực chất là kết quả của các lực khác như lực hấp dẫn, lực căng dây, lực ma sát, hoặc lực điện từ, tùy thuộc vào bối cảnh của bài toán. Điều này có nghĩa là không có một "lực hướng tâm" nào tồn tại độc lập, mà nó là sự kết hợp của các lực khác đã được biết đến.

• Phụ thuộc vào tốc độ và bán kính:

  Như đã biết, lực hướng tâm phụ thuộc vào tốc độ chuyển động của vật thể và bán kính của quỹ đạo theo công thức:

  
  $$F_{ht} = \dfrac{m \cdot v^2}{r}$$

  Điều này có nghĩa là với tốc độ cao hơn hoặc bán kính nhỏ hơn, lực hướng tâm cần thiết để duy trì chuyển động tròn sẽ lớn hơn. Ngược lại, tốc độ giảm hoặc bán kính tăng sẽ làm giảm lực hướng tâm.

• Ứng dụng trong chuyển động tròn đều:

  Trong các chuyển động tròn đều, lực hướng tâm đóng vai trò không thể thiếu để giữ cho vật thể tiếp tục di chuyển theo quỹ đạo mà không bị lệch hướng. Nó duy trì sự ổn định của chuyển động, đảm bảo vật thể không bị văng ra ngoài hoặc rơi vào trong quỹ đạo.

Hiểu biết về các tính chất này giúp ta có cái nhìn sâu sắc hơn về cách lực hướng tâm hoạt động và ứng dụng trong thực tế, từ việc dự đoán chuyển động của các vật thể trong môi trường thiên nhiên đến thiết kế các hệ thống kỹ thuật phức tạp.

Các bài tập về lực hướng tâm giúp người học củng cố kiến thức và hiểu rõ hơn về cách áp dụng lý thuyết vào thực tế. Dưới đây là một số bài tập tiêu biểu liên quan đến lực hướng tâm, được thiết kế từ cơ bản đến nâng cao để đáp ứng nhu cầu học tập và rèn luyện:

1. Bài tập 1: Tính lực hướng tâm của một vật chuyển động tròn đều

   Một vật có khối lượng \(m = 2 \, \text{kg}\) chuyển động tròn đều với vận tốc \(v = 4 \, \text{m/s}\) trên quỹ đạo có bán kính \(r = 0,5 \, \text{m}\). Tính lực hướng tâm tác dụng lên vật.

   Giải:

   Áp dụng công thức lực hướng tâm:

   
   $$F_{ht} = \dfrac{m \cdot v^2}{r} = \dfrac{2 \cdot 4^2}{0,5} = 64 \, \text{N}$$

   Vậy lực hướng tâm tác dụng lên vật là \(64 \, \text{N}\).

2. Bài tập 2: Xác định vận tốc cần thiết để vật không bị rơi

   Một xe đua chuyển động trên đường cong có bán kính \(r = 100 \, \text{m}\). Tính vận tốc lớn nhất mà xe có thể di chuyển mà không bị trượt ra ngoài nếu hệ số ma sát giữa lốp xe và mặt đường là \( \mu = 0,3 \).

   Giải:

   Áp dụng công thức lực ma sát đóng vai trò lực hướng tâm:

   
   $$F_{ht} = \mu \cdot m \cdot g$$

   Với \(F_{ht} = \dfrac{m \cdot v^2}{r}\), ta có:

   
   $$\dfrac{m \cdot v^2}{r} = \mu \cdot m \cdot g$$

   
   $$v^2 = \mu \cdot g \cdot r$$

   
   $$v = \sqrt{\mu \cdot g \cdot r} = \sqrt{0,3 \cdot 9,8 \cdot 100} \approx 17,15 \, \text{m/s}$$

   Vậy vận tốc lớn nhất mà xe có thể di chuyển là \(17,15 \, \text{m/s}\).

3. Bài tập 3: Tính bán kính quỹ đạo khi biết lực hướng tâm và vận tốc

   Một vệ tinh có khối lượng \(m = 500 \, \text{kg}\) đang quay quanh Trái Đất với vận tốc \(v = 7,8 \, \text{km/s}\). Lực hướng tâm tác dụng lên vệ tinh là \(F_{ht} = 30 \, \text{kN}\). Tính bán kính quỹ đạo của vệ tinh.

   Giải:

   Áp dụng công thức lực hướng tâm:

   
   $$F_{ht} = \dfrac{m \cdot v^2}{r}$$

   Ta có:

   
   $$r = \dfrac{m \cdot v^2}{F_{ht}} = \dfrac{500 \cdot (7,8 \times 10^3)^2}{30 \times 10^3}$$

   
   $$r \approx 1,01 \times 10^6 \, \text{m}$$

   Vậy bán kính quỹ đạo của vệ tinh là khoảng \(1,01 \times 10^6 \, \text{m}\).

Những bài tập trên giúp người học rèn luyện khả năng tính toán và hiểu sâu hơn về cách lực hướng tâm hoạt động trong các tình huống thực tế.