Chủ đề vật lý 10 lực hướng tâm: Lực hướng tâm là một khái niệm quan trọng trong chương trình Vật lý lớp 10, đóng vai trò then chốt trong việc hiểu rõ chuyển động tròn. Bài viết này sẽ giúp bạn khám phá sâu hơn về khái niệm lực hướng tâm, công thức tính toán, cũng như những ứng dụng thực tế trong đời sống hàng ngày và kỹ thuật.
Mục lục
Lực Hướng Tâm Trong Vật Lý Lớp 10
Lực hướng tâm là khái niệm cơ bản trong chương trình Vật lý lớp 10, liên quan đến các vật chuyển động tròn đều. Dưới đây là những thông tin chi tiết và đầy đủ nhất về lực hướng tâm.
1. Khái Niệm Lực Hướng Tâm
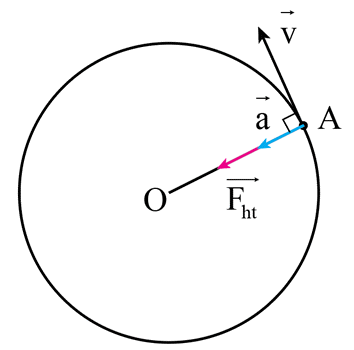
Lực hướng tâm là lực tác dụng vào một vật khi nó chuyển động tròn đều, làm cho vật có gia tốc hướng về tâm của quỹ đạo. Lực này không phải là một lực mới, mà là kết quả của một hoặc nhiều lực khác nhau đã tác dụng lên vật.
2. Công Thức Tính Lực Hướng Tâm
Công thức tổng quát để tính lực hướng tâm được biểu diễn như sau:
\[
F_{ht} = \frac{m \cdot v^2}{R} = m \cdot \omega^2 \cdot R
\]
Trong đó:
- \( F_{ht} \): Lực hướng tâm (N)
- \( m \): Khối lượng của vật (kg)
- \( v \): Vận tốc của vật (m/s)
- \( R \): Bán kính quỹ đạo (m)
- \( \omega \): Tốc độ góc của vật (rad/s)
3. Các Ứng Dụng Thực Tế
Lực hướng tâm có nhiều ứng dụng trong thực tế, như:
- Các vệ tinh nhân tạo chuyển động quanh Trái Đất dưới tác dụng của lực hấp dẫn đóng vai trò là lực hướng tâm.
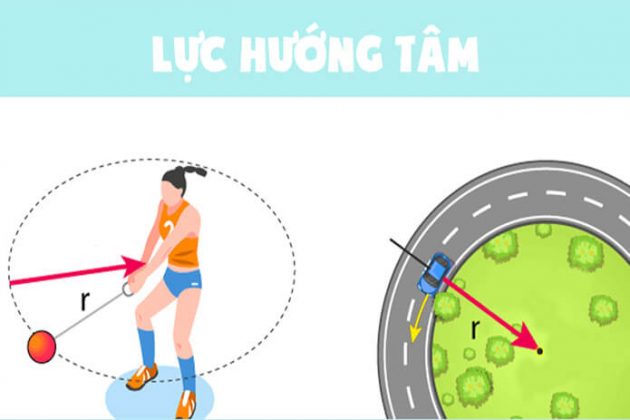
- Ô tô khi di chuyển trên đường cong cũng phải chịu tác dụng của lực hướng tâm để không bị trượt ra khỏi đường.
- Các vận động viên ném tạ phải quay tạ để tạo lực hướng tâm trước khi ném.
4. Ví Dụ Minh Họa
Dưới đây là một số ví dụ minh họa để giúp bạn hiểu rõ hơn về lực hướng tâm:
| Ví dụ 1 | Buộc một vật khối lượng \( m = 100 \, g \) vào một sợi dây dài \( 50 \, cm \), quay cho vật chuyển động tròn đều trong mặt phẳng nằm ngang. Tính lực căng dây tại vị trí thấp nhất trên quỹ đạo. |
| Giải | Áp dụng công thức tính lực hướng tâm và lực căng dây để xác định giá trị lực căng. |
| Ví dụ 2 | Ô tô chuyển động tròn trên một đoạn đường cong có bán kính \( R = 50 \, m \) với vận tốc \( v = 20 \, m/s \). Tính lực ma sát cần thiết để xe không bị trượt. |
| Giải | Áp dụng công thức tính lực hướng tâm và điều kiện cân bằng để xác định lực ma sát. |
5. Lưu Ý Khi Học Về Lực Hướng Tâm
Học sinh cần lưu ý rằng lực hướng tâm không phải là một loại lực mới mà là tổng hợp của các lực tác dụng lên vật. Để hiểu rõ hơn, cần thực hành nhiều bài tập và liên hệ với các hiện tượng thực tế.

.png)
1. Giới Thiệu Về Lực Hướng Tâm
Lực hướng tâm là một khái niệm quan trọng trong vật lý, đặc biệt khi nói về chuyển động tròn đều. Đây là lực giữ cho một vật di chuyển theo quỹ đạo tròn, luôn hướng vào tâm của quỹ đạo đó. Hiểu rõ về lực hướng tâm giúp chúng ta giải thích được nhiều hiện tượng tự nhiên và ứng dụng trong đời sống hàng ngày.
Khi một vật chuyển động tròn đều, nó phải chịu một lực luôn hướng vào tâm của quỹ đạo, gọi là lực hướng tâm. Công thức cơ bản của lực hướng tâm được biểu diễn như sau:
\[
F_{ht} = \frac{m \cdot v^2}{R}
\]
Trong đó:
- \( F_{ht} \): Lực hướng tâm (Newton)
- \( m \): Khối lượng của vật (kilogram)
- \( v \): Vận tốc của vật (mét/giây)
- \( R \): Bán kính của quỹ đạo (mét)
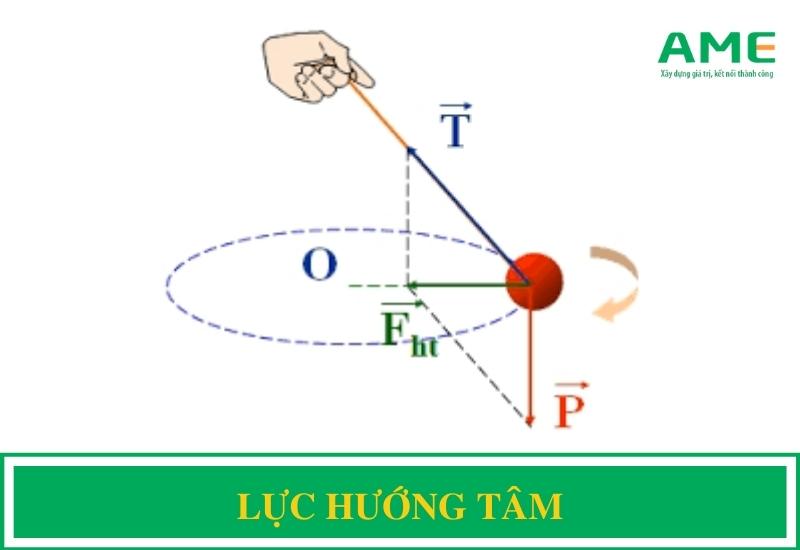
Lực hướng tâm không phải là một loại lực riêng biệt, mà là kết quả của các lực khác như lực ma sát, lực hấp dẫn, hoặc lực căng dây. Để một vật có thể chuyển động tròn đều, phải có một lực tác dụng lên nó để bù đắp cho lực ly tâm - lực có xu hướng đẩy vật ra khỏi quỹ đạo tròn.
Hiểu về lực hướng tâm giúp bạn giải thích được nhiều hiện tượng như việc các hành tinh quay quanh mặt trời, hay việc các phương tiện giao thông di chuyển trên các cung đường cong. Lực này không chỉ là một phần của lý thuyết mà còn có rất nhiều ứng dụng thực tiễn trong đời sống và kỹ thuật.
3. Các Yếu Tố Ảnh Hưởng Đến Lực Hướng Tâm
Lực hướng tâm của một vật trong chuyển động tròn không chỉ phụ thuộc vào một yếu tố duy nhất mà bị ảnh hưởng bởi nhiều yếu tố khác nhau. Dưới đây là các yếu tố quan trọng nhất ảnh hưởng đến lực hướng tâm:
- Khối Lượng Của Vật (\( m \)): Lực hướng tâm tỷ lệ thuận với khối lượng của vật. Khi khối lượng tăng, lực hướng tâm cần thiết để giữ cho vật di chuyển theo quỹ đạo tròn cũng tăng theo.
- Vận Tốc Của Vật (\( v \)): Vận tốc của vật có ảnh hưởng lớn đến lực hướng tâm. Cụ thể, lực hướng tâm tỷ lệ thuận với bình phương của vận tốc. Điều này có nghĩa là nếu vận tốc tăng gấp đôi, lực hướng tâm sẽ tăng lên gấp bốn lần.
- Bán Kính Của Quỹ Đạo (\( R \)): Lực hướng tâm tỷ lệ nghịch với bán kính của quỹ đạo. Khi bán kính giảm, lực hướng tâm sẽ tăng lên và ngược lại. Điều này lý giải tại sao trong các vòng cua gắt, các phương tiện cần một lực lớn hơn để duy trì quỹ đạo tròn.
Các yếu tố này tương tác với nhau theo công thức:
\[
F_{ht} = \frac{m \cdot v^2}{R}
\]
Điều này có nghĩa là để duy trì một lực hướng tâm không đổi, khi một yếu tố thay đổi, các yếu tố khác cũng phải điều chỉnh tương ứng. Ví dụ, nếu bán kính quỹ đạo giảm, để giữ cho lực hướng tâm không đổi, vận tốc của vật cần phải giảm xuống.
Hiểu rõ các yếu tố này không chỉ giúp chúng ta nắm vững kiến thức về chuyển động tròn đều mà còn có thể áp dụng vào các tình huống thực tế như thiết kế đường cong trong giao thông, hoặc tính toán lực cần thiết trong các hệ thống cơ khí.

4. Ứng Dụng Của Lực Hướng Tâm
Lực hướng tâm không chỉ là một khái niệm lý thuyết trong vật lý mà còn có nhiều ứng dụng quan trọng trong đời sống và công nghệ. Dưới đây là một số ứng dụng tiêu biểu của lực hướng tâm:
- Trong Giao Thông: Lực hướng tâm đóng vai trò quan trọng trong việc thiết kế các khúc cua của đường cao tốc. Khi xe di chuyển qua khúc cua, lực hướng tâm giúp xe giữ được quỹ đạo của nó mà không bị văng ra khỏi đường. Điều này đặc biệt quan trọng khi thiết kế các con đường trên núi hay các đường đua.
- Trong Công Nghệ Hàng Không: Khi máy bay thực hiện các cú quay gấp hoặc bay vòng tròn, lực hướng tâm là lực giữ cho máy bay duy trì quỹ đạo bay của nó. Điều này rất quan trọng trong việc điều khiển hướng bay và đảm bảo an toàn cho máy bay.
- Trong Thiết Kế Các Thiết Bị Ly Tâm: Lực hướng tâm được sử dụng trong các thiết bị ly tâm để tách các thành phần khác nhau của hỗn hợp. Ví dụ, trong y học, các máy ly tâm được sử dụng để tách các thành phần của máu hoặc các dung dịch khác.
- Trong Các Trò Chơi Giải Trí: Các trò chơi như tàu lượn siêu tốc sử dụng lực hướng tâm để tạo ra cảm giác mạnh cho người chơi khi quay ở tốc độ cao. Lực này giúp giữ cho người chơi an toàn trong ghế của họ trong suốt quá trình di chuyển.
Lực hướng tâm là một yếu tố cơ bản nhưng rất quan trọng trong nhiều lĩnh vực khác nhau. Việc hiểu rõ về lực hướng tâm không chỉ giúp chúng ta hiểu sâu hơn về các hiện tượng vật lý mà còn ứng dụng vào nhiều khía cạnh của cuộc sống và công nghệ hiện đại.

5. Bài Tập Minh Họa Và Giải Chi Tiết
Dưới đây là một số bài tập minh họa về lực hướng tâm, cùng với lời giải chi tiết giúp bạn hiểu rõ hơn về khái niệm này và cách áp dụng công thức vào thực tế.
Bài Tập 1: Tính Lực Hướng Tâm Trên Quỹ Đạo Tròn
Một vật có khối lượng \( m = 2 \, \text{kg} \) chuyển động với vận tốc \( v = 10 \, \text{m/s} \) trên quỹ đạo tròn bán kính \( R = 5 \, \text{m} \). Tính lực hướng tâm tác dụng lên vật.
Lời Giải:
Áp dụng công thức tính lực hướng tâm:
\[
F_{ht} = \frac{m \cdot v^2}{R}
\]
Thay các giá trị đã cho vào công thức:
\[
F_{ht} = \frac{2 \cdot 10^2}{5} = \frac{200}{5} = 40 \, \text{N}
\]
Vậy lực hướng tâm tác dụng lên vật là \( 40 \, \text{N} \).
Bài Tập 2: Tính Vận Tốc Khi Biết Lực Hướng Tâm
Một vật có khối lượng \( m = 1 \, \text{kg} \) chịu tác dụng của lực hướng tâm \( F_{ht} = 25 \, \text{N} \) trên quỹ đạo tròn bán kính \( R = 2 \, \text{m} \). Tính vận tốc của vật.
Lời Giải:
Áp dụng công thức tính lực hướng tâm và giải để tìm vận tốc:
\[
v = \sqrt{\frac{F_{ht} \cdot R}{m}}
\]
Thay các giá trị đã cho vào công thức:
\[
v = \sqrt{\frac{25 \cdot 2}{1}} = \sqrt{50} \approx 7.07 \, \text{m/s}
\]
Vậy vận tốc của vật là \( 7.07 \, \text{m/s} \).
Bài Tập 3: Tính Bán Kính Quỹ Đạo Khi Biết Vận Tốc Và Lực Hướng Tâm
Một vật có khối lượng \( m = 0.5 \, \text{kg} \) chuyển động với vận tốc \( v = 8 \, \text{m/s} \) và chịu tác dụng của lực hướng tâm \( F_{ht} = 32 \, \text{N} \). Tính bán kính quỹ đạo của vật.
Lời Giải:
Áp dụng công thức tính lực hướng tâm và giải để tìm bán kính quỹ đạo:
\[
R = \frac{m \cdot v^2}{F_{ht}}
\]
Thay các giá trị đã cho vào công thức:
\[
R = \frac{0.5 \cdot 8^2}{32} = \frac{32}{32} = 1 \, \text{m}
\]
Vậy bán kính quỹ đạo của vật là \( 1 \, \text{m} \).
Các bài tập này giúp củng cố kiến thức về lực hướng tâm và cách áp dụng công thức trong các tình huống khác nhau. Bằng cách giải các bài tập này, bạn sẽ nắm vững hơn về khái niệm và ứng dụng của lực hướng tâm trong vật lý.

6. Lưu Ý Khi Học Và Ứng Dụng Lực Hướng Tâm
Khi học và áp dụng kiến thức về lực hướng tâm, học sinh cần lưu ý một số điểm quan trọng để tránh hiểu lầm và áp dụng sai nguyên lý. Dưới đây là những lưu ý cụ thể:
6.1 Những Sai Lầm Thường Gặp
- Hiểu nhầm bản chất của lực hướng tâm: Nhiều học sinh có xu hướng coi lực hướng tâm là một lực mới. Thực tế, lực hướng tâm không phải là một loại lực riêng biệt mà là hợp lực của các lực đã biết (như lực hấp dẫn, lực ma sát, lực căng dây) có xu hướng kéo vật về tâm của quỹ đạo chuyển động tròn.
- Không xem xét đầy đủ các lực: Khi giải các bài toán liên quan đến lực hướng tâm, học sinh thường chỉ tập trung vào lực hướng tâm mà quên đi các lực khác cũng có ảnh hưởng đến chuyển động của vật, dẫn đến sai lầm trong tính toán và phân tích.
- Lạm dụng công thức: Một số học sinh thường áp dụng các công thức tính lực hướng tâm mà không kiểm tra điều kiện áp dụng hoặc không hiểu rõ nguồn gốc của công thức, dẫn đến kết quả sai lệch.
6.2 Phương Pháp Học Hiệu Quả
- Nắm vững lý thuyết cơ bản: Trước khi giải các bài tập phức tạp, học sinh cần hiểu rõ khái niệm, bản chất và các đặc điểm của lực hướng tâm, cũng như các lực có thể đóng vai trò lực hướng tâm.
- Phân tích kỹ lưỡng tình huống thực tế: Khi đối mặt với các bài toán thực tế, hãy dành thời gian để xác định các lực tác dụng lên vật và xem xét liệu lực nào đang đóng vai trò lực hướng tâm. Điều này giúp đảm bảo việc áp dụng công thức và giải pháp được chính xác.
- Thực hành đa dạng bài tập: Học sinh nên rèn luyện với nhiều dạng bài tập khác nhau, từ cơ bản đến nâng cao, bao gồm các bài tập liên quan đến chuyển động li tâm và ứng dụng của lực hướng tâm trong thực tế. Điều này không chỉ giúp củng cố kiến thức mà còn nâng cao khả năng áp dụng vào các tình huống thực tế.
- Liên hệ với các hiện tượng thực tiễn: Việc liên hệ các bài học với các hiện tượng trong cuộc sống, như chuyển động của ô tô khi đi qua đoạn đường cong hoặc chuyển động của vệ tinh quanh Trái Đất, giúp học sinh hiểu sâu hơn và ghi nhớ lâu hơn.
Việc hiểu đúng và áp dụng chính xác các kiến thức về lực hướng tâm không chỉ giúp học sinh đạt kết quả cao trong học tập mà còn là nền tảng để hiểu sâu hơn về các hiện tượng vật lý trong cuộc sống và công nghệ.