Biểu Thức Đúng Về Lực Hướng Tâm: Tất Cả Những Điều Bạn Cần Biết

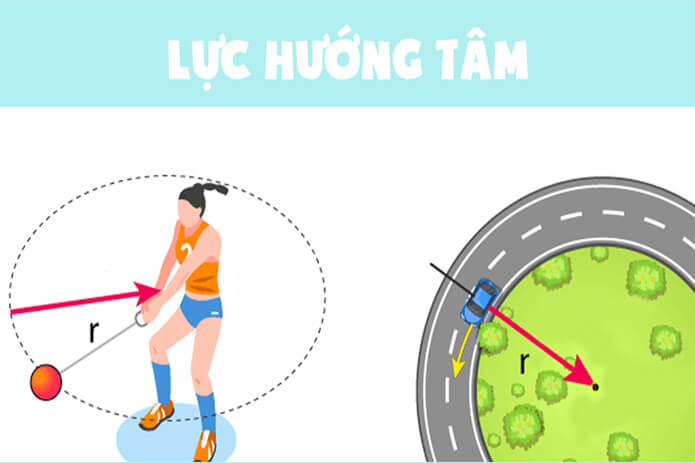
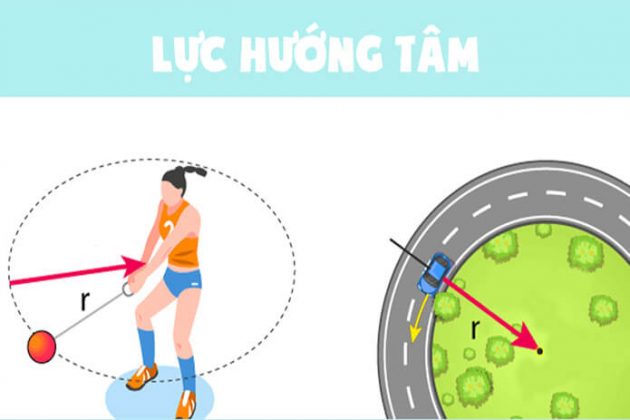
Lực hướng tâm là một lực cơ bản trong vật lý, thường xuất hiện khi một vật chuyển động tròn đều quanh một điểm cố định. Lực này luôn hướng về tâm của quỹ đạo chuyển động, giữ cho vật không bị văng ra ngoài. Để hiểu rõ hơn về lực hướng tâm, chúng ta có thể xem xét các biểu thức và ứng dụng thực tế liên quan đến nó.

Công Thức Lực Hướng Tâm

Công thức cơ bản của lực hướng tâm được biểu diễn như sau:

$$
F

ht


=


m

v
2


r

Trong đó:

• F_ht: Lực hướng tâm (N)
• m: Khối lượng của vật (kg)
• v: Vận tốc của vật (m/s)
• r: Bán kính quỹ đạo (m)

Ví Dụ Ứng Dụng Lực Hướng Tâm

1. Thiết Kế Đường Cong Trên Đường: Lực hướng tâm được sử dụng để thiết kế độ nghiêng của mặt đường tại các khúc cua, giúp xe cộ di chuyển an toàn mà không bị trượt ra khỏi quỹ đạo.
2. Máy Quay Ly Tâm: Trong các ngành công nghiệp, lực hướng tâm giúp tách các thành phần trong hỗn hợp dựa trên khối lượng của chúng.
3. Vệ Tinh Nhân Tạo: Lực hấp dẫn giữa Trái Đất và vệ tinh đóng vai trò là lực hướng tâm, giữ vệ tinh trên quỹ đạo.
4. Công Viên Giải Trí: Lực hướng tâm giữ vai trò quan trọng trong việc vận hành các thiết bị như vòng quay hay tàu lượn, đảm bảo an toàn cho người sử dụng.

Bài Tập Vận Dụng

Dưới đây là một số bài tập áp dụng công thức lực hướng tâm:

• Bài Tập 1: Tính lực hướng tâm của một vật có khối lượng 1kg, chuyển động tròn đều với vận tốc 5m/s trên quỹ đạo bán kính 2m.
• Bài Tập 2: Xác định độ lớn của lực hướng tâm khi một chiếc xe chuyển động qua đoạn đường cong bán kính 100m với vận tốc 36km/h.
• Bài Tập 3: Tính áp lực mà một vật tạo ra ở điểm cao nhất của vòng cầu khi nó di chuyển với vận tốc không đổi.

Kết Luận

Hiểu rõ về lực hướng tâm và cách tính toán nó là rất quan trọng trong việc áp dụng vào thực tế, từ thiết kế hạ tầng giao thông cho đến các ứng dụng công nghiệp và khoa học. Việc nắm vững biểu thức đúng về lực hướng tâm không chỉ giúp giải quyết các bài toán vật lý mà còn giúp chúng ta ứng dụng vào nhiều lĩnh vực khác nhau trong cuộc sống.

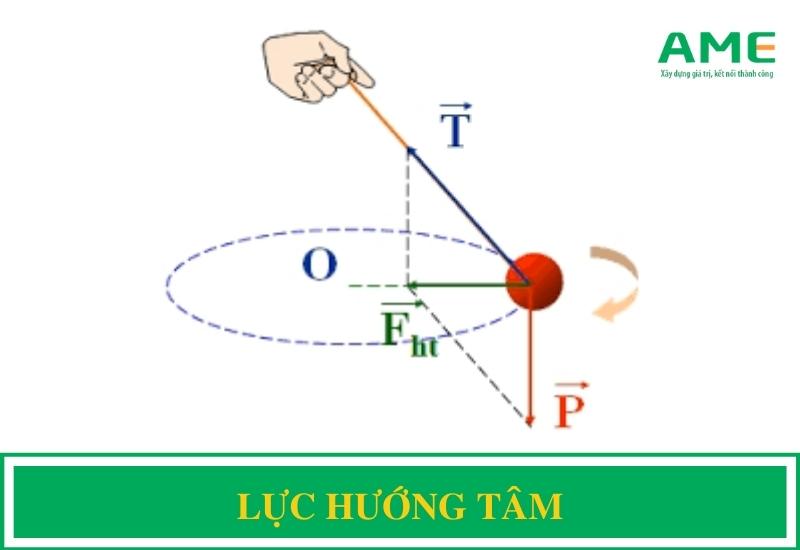
Lực hướng tâm là một khái niệm quan trọng trong Vật lý, đặc biệt trong lĩnh vực chuyển động tròn đều. Đây là lực giữ cho một vật chuyển động theo quỹ đạo tròn, luôn hướng vào tâm của quỹ đạo đó. Lực hướng tâm không phải là một loại lực mới mà là sự tổng hợp của các lực khác đã tác dụng lên vật theo phương bán kính và hướng vào tâm.

Khi một vật chuyển động tròn đều, lực hướng tâm có thể được xác định thông qua biểu thức:

\( F_{ht} = \dfrac{mv^2}{r} = m\omega^2 r \)

• m: khối lượng của vật (kg)
• v: vận tốc tuyến tính của vật (m/s)
• r: bán kính quỹ đạo tròn (m)
• \(\omega\): vận tốc góc (rad/s)

Lực hướng tâm có thể được tạo ra bởi nhiều loại lực khác nhau, tùy thuộc vào bối cảnh của bài toán. Ví dụ, trong trường hợp của một vật quay quanh Trái Đất, lực hướng tâm là lực hấp dẫn giữa vật và Trái Đất. Trong một bài toán liên quan đến chuyển động của xe trên cầu vượt, lực hướng tâm có thể là sự kết hợp giữa lực ma sát và lực hấp dẫn.

Để hiểu rõ hơn, hãy cùng xem xét các ví dụ cụ thể trong các phần tiếp theo.

Công thức và biểu thức của lực hướng tâm là những yếu tố cơ bản giúp hiểu rõ hơn về cách lực này hoạt động trong chuyển động tròn. Dưới đây là các công thức và biểu thức quan trọng mà bạn cần nắm vững:

2.1. Công thức tổng quát của lực hướng tâm

Lực hướng tâm \( F_{ht} \) có thể được tính thông qua công thức sau:

\( F_{ht} = \dfrac{mv^2}{r} \)

• m: khối lượng của vật (kg)
• v: vận tốc tuyến tính của vật (m/s)
• r: bán kính của quỹ đạo tròn (m)

Công thức này thể hiện rằng lực hướng tâm tỉ lệ thuận với khối lượng của vật, bình phương vận tốc của vật và tỉ lệ nghịch với bán kính của quỹ đạo.

2.2. Biểu thức lực hướng tâm dưới dạng vận tốc góc

Nếu biết vận tốc góc \( \omega \), chúng ta có thể tính lực hướng tâm theo biểu thức:

\( F_{ht} = m\omega^2 r \)

• \(\omega\): vận tốc góc (rad/s)
• r: bán kính của quỹ đạo tròn (m)

Biểu thức này cho thấy lực hướng tâm cũng tỉ lệ thuận với bình phương vận tốc góc và bán kính quỹ đạo.

2.3. Mối quan hệ giữa lực hướng tâm và các đại lượng liên quan

Trong chuyển động tròn đều, lực hướng tâm có mối liên hệ chặt chẽ với các đại lượng khác như gia tốc hướng tâm \( a_{ht} \) và thời gian chu kỳ \( T \).

• Gia tốc hướng tâm \( a_{ht} \) được xác định bằng:

\( a_{ht} = \dfrac{v^2}{r} = \omega^2 r \)

• Chu kỳ chuyển động \( T \) có liên hệ với vận tốc góc qua biểu thức:

\( T = \dfrac{2\pi}{\omega} \)

Như vậy, lực hướng tâm có thể được diễn đạt qua nhiều biểu thức khác nhau tùy thuộc vào thông tin mà bài toán cung cấp. Việc hiểu rõ các công thức và biểu thức này sẽ giúp bạn giải quyết các bài toán liên quan đến lực hướng tâm một cách hiệu quả.

Lực hướng tâm là một khái niệm cơ bản trong Vật lý và có rất nhiều ứng dụng trong thực tế. Dưới đây là một số bài toán ứng dụng tiêu biểu giúp bạn hiểu rõ hơn về cách tính toán và áp dụng lực hướng tâm trong các tình huống cụ thể.

3.1. Tính lực hướng tâm trong chuyển động tròn đều

Giả sử một vật có khối lượng \(m\) chuyển động tròn đều với vận tốc \(v\) trên quỹ đạo bán kính \(r\). Lực hướng tâm \( F_{ht} \) tác dụng lên vật được tính bằng:

\( F_{ht} = \dfrac{mv^2}{r} \)

Ví dụ: Một chiếc ô tô có khối lượng 1000 kg đang chuyển động tròn đều trên quỹ đạo có bán kính 50 m với vận tốc 10 m/s. Hãy tính lực hướng tâm tác dụng lên ô tô.

3.2. Ứng dụng lực hướng tâm trong bài toán chuyển động trên mặt phẳng nghiêng

Trong bài toán chuyển động của vật trên mặt phẳng nghiêng, lực hướng tâm đóng vai trò quan trọng trong việc giữ cho vật chuyển động theo quỹ đạo tròn. Giả sử một vật chuyển động trên mặt phẳng nghiêng có bán kính cong \(r\), lực hướng tâm có thể được xác định dựa trên trọng lực và lực ma sát.

3.3. Ứng dụng trong bài toán tính độ biến dạng của lò xo

Khi một vật nặng được gắn vào một lò xo và thực hiện chuyển động tròn, lực hướng tâm được tạo ra do độ biến dạng của lò xo. Độ biến dạng này có thể được tính bằng cách áp dụng định luật Hooke:

\( F_{ht} = k \cdot \Delta x \)

Trong đó, \(k\) là hằng số đàn hồi của lò xo và \(\Delta x\) là độ biến dạng của lò xo.

3.4. Ứng dụng trong bài toán tính áp lực tại các điểm trên quỹ đạo tròn

Khi một vật chuyển động tròn, áp lực mà vật tác dụng lên các điểm trên quỹ đạo có thể thay đổi tùy thuộc vào tốc độ và bán kính quỹ đạo. Lực hướng tâm ở đây giúp tính toán áp lực tại các điểm này, đặc biệt trong các bài toán liên quan đến chuyển động của ô tô hoặc tàu lượn siêu tốc.

Những bài toán trên đây không chỉ giúp củng cố kiến thức về lực hướng tâm mà còn mở rộng khả năng ứng dụng vào nhiều tình huống thực tế, từ đó giúp bạn có cái nhìn toàn diện hơn về lực hướng tâm trong Vật lý.

Để hiểu rõ hơn về cách áp dụng lực hướng tâm trong các bài toán Vật lý, hãy cùng xem xét một số ví dụ cụ thể dưới đây. Những ví dụ này sẽ giúp bạn nắm bắt rõ hơn cách tính toán và ứng dụng lực hướng tâm trong thực tế.

4.1. Ví dụ về bài toán chuyển động tròn đều

Giả sử một vật có khối lượng 2 kg chuyển động tròn đều với vận tốc 5 m/s trên quỹ đạo có bán kính 3 m. Tính lực hướng tâm tác dụng lên vật.

Giải:

Ta sử dụng công thức:

\( F_{ht} = \dfrac{mv^2}{r} \)

Thay các giá trị đã biết vào:

\( F_{ht} = \dfrac{2 \times 5^2}{3} = \dfrac{50}{3} \approx 16.67 \, \text{N} \)

Vậy lực hướng tâm tác dụng lên vật là 16.67 N.

4.2. Ví dụ về bài toán lực hướng tâm trong hệ thống lò xo

Một vật nặng 0.5 kg gắn vào đầu một lò xo, chuyển động tròn đều trên mặt phẳng ngang với bán kính 0.2 m. Biết rằng độ cứng của lò xo là 100 N/m, hãy tính độ biến dạng của lò xo.

Giải:

Lực hướng tâm được cung cấp bởi lực đàn hồi của lò xo, do đó:

\( F_{ht} = k \cdot \Delta x = \dfrac{mv^2}{r} \)

Vì \( v = \omega \cdot r \), ta có:

\( k \cdot \Delta x = m \cdot \omega^2 \cdot r \)

Giải phương trình trên để tìm \( \Delta x \):

\( \Delta x = \dfrac{m \cdot \omega^2 \cdot r}{k} \)

4.3. Ví dụ về bài toán tính lực hướng tâm trong chuyển động của ô tô qua cầu

Một chiếc ô tô có khối lượng 1200 kg di chuyển qua một chiếc cầu hình cung với bán kính 50 m. Tại điểm cao nhất của cầu, tính lực hướng tâm tác dụng lên ô tô nếu vận tốc của ô tô là 10 m/s.

Giải:

Tại điểm cao nhất, lực hướng tâm là lực tổng hợp của trọng lực và phản lực từ mặt cầu. Sử dụng công thức:

\( F_{ht} = \dfrac{mv^2}{r} \)

Thay các giá trị đã biết vào:

\( F_{ht} = \dfrac{1200 \times 10^2}{50} = 2400 \, \text{N} \)

Vậy lực hướng tâm tác dụng lên ô tô tại điểm cao nhất của cầu là 2400 N.

4.4. Ví dụ về lực hướng tâm trong chuyển động của vệ tinh nhân tạo

Một vệ tinh nhân tạo có khối lượng 1000 kg chuyển động quanh Trái Đất theo quỹ đạo tròn với bán kính 7000 km. Tính lực hướng tâm tác dụng lên vệ tinh, biết vận tốc của vệ tinh là 7.8 km/s.

Giải:

Sử dụng công thức:

\( F_{ht} = \dfrac{mv^2}{r} \)

Thay các giá trị đã biết vào:

\( F_{ht} = \dfrac{1000 \times (7.8 \times 10^3)^2}{7000 \times 10^3} \approx 87.43 \, \text{kN} \)

Vậy lực hướng tâm tác dụng lên vệ tinh là khoảng 87.43 kN.

Khi giải các bài toán liên quan đến lực hướng tâm, có một số lưu ý quan trọng mà bạn cần nhớ để đảm bảo tính chính xác và hiệu quả trong quá trình tính toán. Dưới đây là các lưu ý cần thiết:

5.1. Xác định đúng lực tác dụng tạo ra lực hướng tâm

Lực hướng tâm không phải là một lực mới mà là kết quả của một hoặc nhiều lực khác như lực ma sát, lực đàn hồi, lực hấp dẫn, hoặc lực điện từ. Do đó, bạn cần xác định đúng lực nào trong bài toán là nguyên nhân tạo ra lực hướng tâm.

5.2. Sử dụng biểu thức phù hợp với thông tin đề bài

Trong một số bài toán, bạn có thể sử dụng các biểu thức khác nhau để tính lực hướng tâm, chẳng hạn:

• Sử dụng công thức \( F_{ht} = \dfrac{mv^2}{r} \) khi biết vận tốc tuyến tính \(v\) và bán kính \(r\).
• Sử dụng công thức \( F_{ht} = m\omega^2 r \) khi biết vận tốc góc \( \omega \).

Lựa chọn biểu thức phù hợp sẽ giúp bạn tính toán nhanh chóng và chính xác hơn.

5.3. Kiểm tra đơn vị đo

Đảm bảo rằng các đại lượng đầu vào như khối lượng, vận tốc, và bán kính đều sử dụng cùng một hệ đơn vị. Nếu cần thiết, hãy chuyển đổi các đơn vị về cùng một hệ trước khi tính toán.

5.4. Lưu ý về hướng của lực hướng tâm

Lực hướng tâm luôn hướng vào tâm của quỹ đạo tròn. Điều này có nghĩa là trong các bài toán về động lực học, bạn cần chú ý đến hướng của lực khi lập phương trình cân bằng lực hoặc khi phân tích chuyển động.

5.5. Xem xét các yếu tố gây ảnh hưởng đến lực hướng tâm

Trong một số bài toán thực tế, các yếu tố như ma sát, sức cản không khí hoặc độ cứng của vật liệu có thể ảnh hưởng đến lực hướng tâm. Cần cân nhắc và đưa vào các yếu tố này nếu bài toán yêu cầu.

Những lưu ý trên sẽ giúp bạn giải quyết các bài toán liên quan đến lực hướng tâm một cách chính xác và hiệu quả hơn. Hãy luôn kiểm tra kỹ lưỡng các bước giải để tránh những sai sót không đáng có.