Công Thức Tính Độ Lớn Lực Hướng Tâm: Hướng Dẫn Chi Tiết Và Ví Dụ Minh Họa

Lực hướng tâm là lực cần thiết để giữ cho một vật di chuyển theo quỹ đạo tròn đều. Độ lớn của lực này được xác định bởi vận tốc, khối lượng của vật và bán kính của quỹ đạo. Công thức tính độ lớn lực hướng tâm được biểu diễn như sau:

1. Định Nghĩa Lực Hướng Tâm

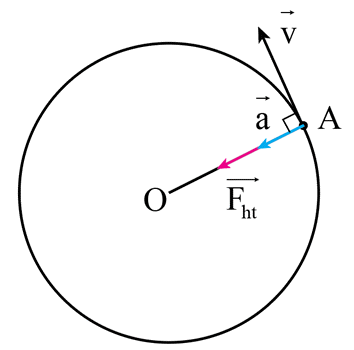
Lực hướng tâm là lực (hay hợp lực của các lực) tác dụng vào một vật đang chuyển động tròn đều và gây ra gia tốc hướng tâm, giúp vật giữ quỹ đạo tròn. Lực hướng tâm luôn hướng về tâm của quỹ đạo.

2. Công Thức Tính Độ Lớn Lực Hướng Tâm

Công thức tổng quát để tính lực hướng tâm là:

F_{ht} = \dfrac{mv^2}{r}

Trong đó:

• F_{ht} là độ lớn của lực hướng tâm (N).
• m là khối lượng của vật (kg).
• v là vận tốc của vật khi di chuyển theo quỹ đạo tròn (m/s).
• r là bán kính của quỹ đạo tròn (m).

3. Các Ví Dụ Thực Tế

• Vệ Tinh Nhân Tạo: Lực hấp dẫn giữa Trái Đất và vệ tinh nhân tạo đóng vai trò lực hướng tâm, giữ cho vệ tinh chuyển động tròn quanh Trái Đất.
• Chuyển Động Trên Đường Cong: Ô tô di chuyển trên đường cong với tốc độ cao sẽ tạo ra lực hướng tâm để giữ xe trên quỹ đạo của đoạn đường cong.
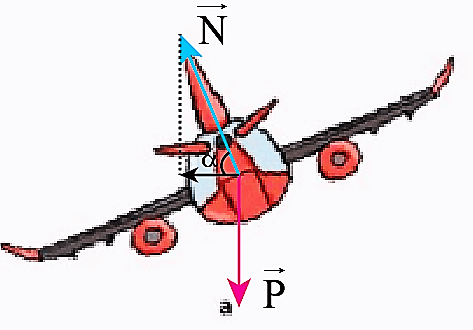
• Quay Vòng Nhào Lộn: Trong nhào lộn, phi công phải chịu một lực hướng tâm lớn khi máy bay thực hiện các vòng quay dốc đứng.

4. Các Ứng Dụng Thực Tế Của Lực Hướng Tâm

Lực hướng tâm không phải là một loại lực riêng biệt mà là kết quả của sự kết hợp giữa các lực như lực hấp dẫn, lực đàn hồi, và lực ma sát. Dưới đây là một số ứng dụng phổ biến của lực hướng tâm:

• Các Công Trình Giao Thông: Thiết kế của các đoạn đường cong, cầu vượt thường phải tính đến lực hướng tâm để đảm bảo an toàn khi xe cộ di chuyển.
• Thiết Bị Quay Ly Tâm: Trong các máy ly tâm, lực hướng tâm được sử dụng để phân tách các thành phần của một chất lỏng dựa trên khối lượng riêng của chúng.
• Chuyển Động Của Hành Tinh: Lực hấp dẫn đóng vai trò lực hướng tâm giữ các hành tinh di chuyển theo quỹ đạo quanh Mặt Trời.

5. Bài Tập Áp Dụng

1. Bài Tập 1: Tính lực hướng tâm tác dụng lên một ô tô có khối lượng 1500kg khi xe di chuyển với vận tốc 72km/h trên đường cong có bán kính 50m.
2. Bài Tập 2: Một vệ tinh có khối lượng 200kg quay quanh Trái Đất ở độ cao 300km với vận tốc 7500m/s. Tính lực hướng tâm tác dụng lên vệ tinh.

Hy vọng thông tin trên sẽ giúp bạn hiểu rõ hơn về lực hướng tâm và cách tính toán nó trong các tình huống thực tế.

Lực hướng tâm là lực cần thiết để duy trì một vật thể chuyển động tròn đều quanh một quỹ đạo. Lực này luôn hướng về phía tâm của quỹ đạo và có giá trị bằng khối lượng của vật nhân với gia tốc hướng tâm.

Trong chuyển động tròn đều, gia tốc hướng tâm được tính bằng:

\[
a_{ht} = \frac{v^2}{r}
\]

Trong đó:

• a_ht: Gia tốc hướng tâm (m/s²)
• v: Vận tốc của vật thể (m/s)
• r: Bán kính của quỹ đạo tròn (m)

Lực hướng tâm được biểu diễn bằng công thức:

\[
F_{ht} = m \times a_{ht} = \frac{m \times v^2}{r}
\]

Trong đó:

• F_ht: Lực hướng tâm (N)
• m: Khối lượng của vật thể (kg)
• v: Vận tốc của vật thể (m/s)
• r: Bán kính của quỹ đạo tròn (m)

Lực hướng tâm là một trong những lực quan trọng trong cơ học, ảnh hưởng đến nhiều hiện tượng vật lý trong đời sống, từ chuyển động của hành tinh quanh Mặt Trời đến chuyển động của xe cộ trên đường cong.

Lực hướng tâm là lực đóng vai trò quan trọng trong chuyển động tròn đều, luôn hướng về phía tâm của quỹ đạo. Để tính toán lực này, chúng ta có thể sử dụng công thức dựa trên gia tốc hướng tâm và khối lượng của vật thể.

Công thức tổng quát để tính lực hướng tâm là:

\[
F_{ht} = m \times a_{ht} = \frac{m \times v^2}{r}
\]

Trong đó:

• F_ht: Lực hướng tâm (N - Newton)
• m: Khối lượng của vật thể (kg)
• v: Vận tốc của vật thể (m/s)
• r: Bán kính của quỹ đạo tròn (m)

Công thức trên cho thấy rằng lực hướng tâm phụ thuộc vào khối lượng của vật, vận tốc của nó và bán kính của quỹ đạo mà nó di chuyển. Nếu vận tốc của vật tăng hoặc bán kính của quỹ đạo giảm, lực hướng tâm sẽ tăng lên. Ngược lại, nếu bán kính quỹ đạo tăng hoặc vận tốc giảm, lực hướng tâm sẽ giảm.

Một cách khác để biểu diễn công thức lực hướng tâm là sử dụng tốc độ góc \(\omega\), trong đó:

\[
F_{ht} = m \times \omega^2 \times r
\]

Trong đó:

• \(\omega\): Tốc độ góc (rad/s)

Cả hai công thức đều có thể áp dụng tùy vào thông số nào đã được cho trước trong bài toán. Việc hiểu và áp dụng đúng công thức sẽ giúp chúng ta giải quyết hiệu quả các bài toán liên quan đến lực hướng tâm.

Để hiểu rõ hơn về cách tính và ứng dụng của lực hướng tâm, chúng ta hãy cùng xem xét một số ví dụ cụ thể:

Ví Dụ 1: Vật Nặng Buộc Vào Dây Chuyển Động Tròn Đều

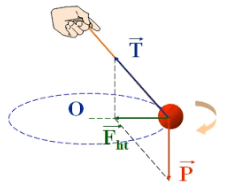
Một vật nặng có khối lượng \( m = 2 \, \text{kg} \) được buộc vào đầu một sợi dây dài \( r = 1 \, \text{m} \). Khi vật được quay tròn đều với vận tốc \( v = 3 \, \text{m/s} \), lực hướng tâm tác dụng lên vật sẽ được tính như sau:

\[
F_{ht} = \frac{m \times v^2}{r} = \frac{2 \times 3^2}{1} = 18 \, \text{N}
\]

Vậy lực hướng tâm tác dụng lên vật là \( 18 \, \text{N} \), hướng vào tâm của quỹ đạo tròn.

Ví Dụ 2: Chuyển Động Của Xe Trên Đường Cong

Một chiếc xe có khối lượng \( m = 1000 \, \text{kg} \) di chuyển trên đường cong có bán kính \( r = 50 \, \text{m} \) với vận tốc \( v = 10 \, \text{m/s} \). Lực hướng tâm cần thiết để xe không bị trượt khỏi đường cong được tính như sau:

\[
F_{ht} = \frac{m \times v^2}{r} = \frac{1000 \times 10^2}{50} = 2000 \, \text{N}
\]

Vậy lực hướng tâm tác dụng lên xe là \( 2000 \, \text{N} \).

Ví Dụ 3: Vệ Tinh Quay Quanh Trái Đất

Một vệ tinh có khối lượng \( m = 500 \, \text{kg} \) quay quanh Trái Đất ở độ cao sao cho bán kính quỹ đạo của nó là \( r = 7000 \, \text{km} \) với tốc độ góc \( \omega = 0,001 \, \text{rad/s} \). Lực hướng tâm giữ vệ tinh trên quỹ đạo được tính bằng công thức:

\[
F_{ht} = m \times \omega^2 \times r = 500 \times 0,001^2 \times 7000000 = 3500 \, \text{N}
\]

Lực hướng tâm cần thiết để giữ vệ tinh trên quỹ đạo là \( 3500 \, \text{N} \).

Dưới đây là một số bài tập vận dụng nhằm giúp bạn củng cố kiến thức về lực hướng tâm. Hãy áp dụng các công thức đã học để giải quyết các bài toán sau:

Bài Tập 1: Tính Lực Hướng Tâm Của Vật Trên Quỹ Đạo Tròn

Một vật có khối lượng \( m = 4 \, \text{kg} \) chuyển động tròn đều với vận tốc \( v = 5 \, \text{m/s} \) trên một quỹ đạo có bán kính \( r = 2 \, \text{m} \). Tính lực hướng tâm tác dụng lên vật.

Gợi ý: Áp dụng công thức \( F_{ht} = \frac{m \times v^2}{r} \).

Bài Tập 2: Tính Tốc Độ Cần Thiết Để Duy Trì Lực Hướng Tâm

Một chiếc xe có khối lượng \( m = 1200 \, \text{kg} \) chuyển động trên đường cong có bán kính \( r = 50 \, \text{m} \). Biết rằng lực hướng tâm tác dụng lên xe là \( F_{ht} = 9600 \, \text{N} \). Tính vận tốc cần thiết để duy trì lực này.

Gợi ý: Sử dụng công thức \( v = \sqrt{\frac{F_{ht} \times r}{m}} \).

Bài Tập 3: Tính Lực Hướng Tâm Trong Hệ Thống Vệ Tinh

Một vệ tinh có khối lượng \( m = 700 \, \text{kg} \) quay quanh Trái Đất ở quỹ đạo có bán kính \( r = 8000 \, \text{km} \) với tốc độ góc \( \omega = 0,002 \, \text{rad/s} \). Tính lực hướng tâm giữ vệ tinh trên quỹ đạo.

Gợi ý: Áp dụng công thức \( F_{ht} = m \times \omega^2 \times r \).

Bài Tập 4: Xác Định Bán Kính Quỹ Đạo Từ Lực Hướng Tâm

Một vật có khối lượng \( m = 2 \, \text{kg} \) di chuyển với vận tốc \( v = 4 \, \text{m/s} \). Nếu lực hướng tâm tác dụng lên vật là \( F_{ht} = 16 \, \text{N} \), hãy xác định bán kính quỹ đạo.

Gợi ý: Sử dụng công thức \( r = \frac{m \times v^2}{F_{ht}} \).

Hãy thử sức với các bài tập trên để nắm vững cách tính toán và ứng dụng lực hướng tâm trong các bài toán thực tế.

Lực hướng tâm xuất hiện trong nhiều tình huống thực tế xung quanh chúng ta, từ việc điều khiển phương tiện giao thông cho đến hoạt động của các thiết bị vũ trụ. Dưới đây là một số tình huống minh họa cụ thể:

• Xe ô tô qua khúc cua: Khi xe ô tô di chuyển qua khúc cua, lực hướng tâm giữ cho xe không bị trượt ra khỏi quỹ đạo. Độ nghiêng của mặt đường và lực ma sát giữa lốp xe và đường đóng vai trò quan trọng trong việc tạo ra lực này.
• Vệ tinh nhân tạo quay quanh Trái Đất: Lực hấp dẫn giữa Trái Đất và vệ tinh đóng vai trò là lực hướng tâm, giúp vệ tinh duy trì quỹ đạo quanh Trái Đất mà không bị bay ra ngoài không gian.
• Đồ vật trên bàn quay: Khi một vật được đặt trên bàn quay, lực ma sát nghỉ giữ cho vật di chuyển tròn đều quanh tâm của bàn quay, tạo ra lực hướng tâm.
• Vòng đu quay: Khi ngồi trên vòng đu quay, người chơi cảm nhận được lực hướng tâm giữ họ di chuyển theo quỹ đạo tròn, không bị văng ra ngoài dù tốc độ quay có tăng lên.

Lực hướng tâm là một trong những khái niệm quan trọng trong vật lý, không chỉ giúp chúng ta hiểu rõ hơn về các chuyển động tròn mà còn có nhiều ứng dụng thực tế trong đời sống. Từ việc đảm bảo an toàn khi lái xe qua khúc cua, đến thiết kế các thiết bị quay như vòng đu quay hay máy ly tâm, nguyên lý của lực hướng tâm đều được áp dụng để tối ưu hóa hiệu suất và đảm bảo an toàn.

• Thiết kế đường cong giao thông: Hiểu về lực hướng tâm giúp các kỹ sư thiết kế đường cong với độ nghiêng và bán kính phù hợp, nhằm đảm bảo an toàn cho phương tiện khi qua khúc cua.
• Ứng dụng trong ngành hàng không vũ trụ: Lực hướng tâm giúp các vệ tinh duy trì quỹ đạo quanh Trái Đất, điều này rất quan trọng trong việc đảm bảo các hoạt động viễn thông và quan sát khí tượng.
• Công nghệ quay ly tâm: Trong y học và công nghiệp, các máy ly tâm sử dụng lực hướng tâm để tách các chất trong hỗn hợp, ví dụ như phân tách tế bào máu hoặc làm sạch nước.
• Thiết kế thiết bị giải trí: Trong các công viên giải trí, nguyên lý của lực hướng tâm được áp dụng để thiết kế các trò chơi như vòng đu quay, đảm bảo trải nghiệm an toàn và thú vị cho người chơi.

Nhìn chung, hiểu và ứng dụng lực hướng tâm không chỉ giúp chúng ta giải quyết các vấn đề lý thuyết mà còn mang lại những lợi ích thực tế đáng kể trong cuộc sống hàng ngày.