Chủ đề lực hướng tâm là gì: Lực hướng tâm là một khái niệm quan trọng trong vật lý, đóng vai trò thiết yếu trong các chuyển động tròn đều. Bài viết này sẽ cung cấp cho bạn một cái nhìn sâu sắc về lực hướng tâm, từ định nghĩa đến các ứng dụng thực tiễn trong cuộc sống hàng ngày và công nghệ hiện đại.
Mục lục
- Lực Hướng Tâm Là Gì?
- Công Thức Tính Lực Hướng Tâm
- Ứng Dụng Của Lực Hướng Tâm
- Ví Dụ Tính Toán Lực Hướng Tâm
- Bài Tập Về Lực Hướng Tâm
- Công Thức Tính Lực Hướng Tâm
- Ứng Dụng Của Lực Hướng Tâm
- Ví Dụ Tính Toán Lực Hướng Tâm
- Bài Tập Về Lực Hướng Tâm
- Ứng Dụng Của Lực Hướng Tâm
- Ví Dụ Tính Toán Lực Hướng Tâm
- Bài Tập Về Lực Hướng Tâm
- Ví Dụ Tính Toán Lực Hướng Tâm
- Bài Tập Về Lực Hướng Tâm
- Bài Tập Về Lực Hướng Tâm
- Giới Thiệu Chung
- So Sánh Lực Hướng Tâm và Lực Ly Tâm
Lực Hướng Tâm Là Gì?
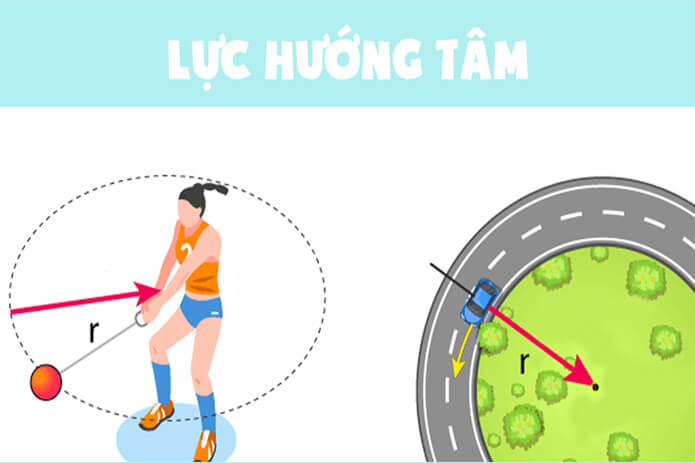
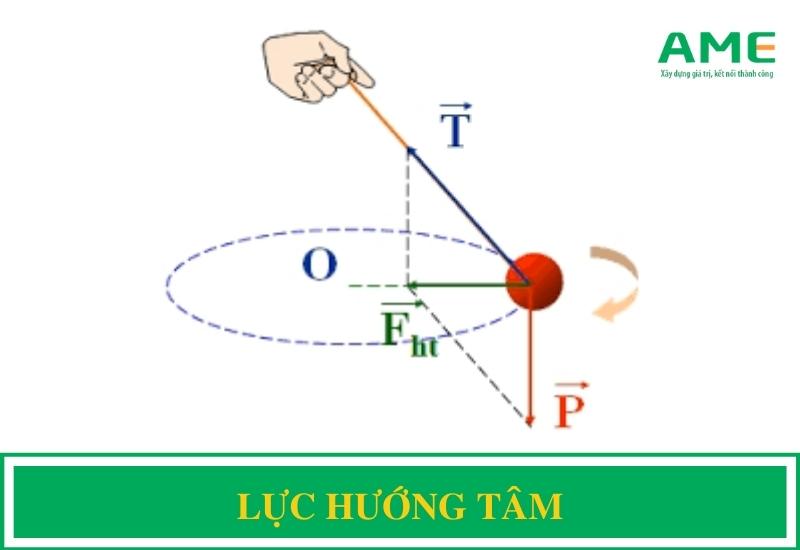
Lực hướng tâm là lực cần thiết để giữ cho một vật di chuyển theo một đường cong hay quỹ đạo tròn. Lực này luôn hướng vào tâm của quỹ đạo và đảm bảo rằng vật không bị văng ra ngoài. Trong nhiều trường hợp, lực hướng tâm không phải là một lực độc lập, mà là kết quả của hợp lực giữa nhiều lực khác nhau như lực ma sát, lực hấp dẫn, hoặc lực đàn hồi.

.png)
Công Thức Tính Lực Hướng Tâm
Lực hướng tâm (Fht) có thể được tính bằng công thức:
\[ F_{ht} = \frac{m \cdot v^2}{r} \]
Trong đó:
- m: Khối lượng của vật (kg)
- v: Vận tốc của vật (m/s)
- r: Bán kính của quỹ đạo (m)
Ứng Dụng Của Lực Hướng Tâm
Lực hướng tâm xuất hiện trong nhiều tình huống trong cuộc sống hàng ngày và kỹ thuật, chẳng hạn như:
- Xe ô tô di chuyển trên đường cong: Khi một xe ô tô quay vòng, lực ma sát giữa bánh xe và mặt đường đóng vai trò như lực hướng tâm.
- Vệ tinh quay quanh Trái đất: Lực hấp dẫn giữa Trái đất và vệ tinh cung cấp lực hướng tâm để vệ tinh duy trì quỹ đạo tròn.
- Con lắc đơn: Khi con lắc di chuyển theo cung tròn, lực căng dây chính là lực hướng tâm.

Ví Dụ Tính Toán Lực Hướng Tâm
Dưới đây là một số ví dụ về cách tính lực hướng tâm trong các tình huống khác nhau:
- Một ô tô có khối lượng 1000 kg di chuyển với vận tốc 20 m/s trên một đường cong có bán kính 50 m. Tính lực hướng tâm tác dụng lên xe.
- Một vệ tinh có khối lượng 500 kg di chuyển trên quỹ đạo cách Trái đất 300 km với vận tốc 7,8 km/s. Tính lực hướng tâm giữ vệ tinh trên quỹ đạo.

XEM THÊM:
Bài Tập Về Lực Hướng Tâm
Bài Tập Trắc Nghiệm
- Lực hướng tâm phụ thuộc vào yếu tố nào sau đây?
- a) Khối lượng của vật
- b) Bán kính của quỹ đạo
- c) Vận tốc của vật
- d) Cả ba yếu tố trên
- Trong trường hợp nào sau đây lực hướng tâm là lớn nhất?
- a) Vật có khối lượng nhỏ, vận tốc lớn, bán kính quỹ đạo nhỏ
- b) Vật có khối lượng lớn, vận tốc nhỏ, bán kính quỹ đạo lớn
- c) Vật có khối lượng lớn, vận tốc lớn, bán kính quỹ đạo nhỏ
- d) Vật có khối lượng nhỏ, vận tốc nhỏ, bán kính quỹ đạo lớn
Bài Tập Tự Luận
- Giải thích tại sao lực hướng tâm là cần thiết để giữ một vật di chuyển theo đường cong.
- Tính lực hướng tâm trong một bài toán cụ thể mà bạn chọn.

Công Thức Tính Lực Hướng Tâm
Lực hướng tâm (Fht) có thể được tính bằng công thức:
\[ F_{ht} = \frac{m \cdot v^2}{r} \]
Trong đó:
- m: Khối lượng của vật (kg)
- v: Vận tốc của vật (m/s)
- r: Bán kính của quỹ đạo (m)
Ứng Dụng Của Lực Hướng Tâm
Lực hướng tâm xuất hiện trong nhiều tình huống trong cuộc sống hàng ngày và kỹ thuật, chẳng hạn như:
- Xe ô tô di chuyển trên đường cong: Khi một xe ô tô quay vòng, lực ma sát giữa bánh xe và mặt đường đóng vai trò như lực hướng tâm.
- Vệ tinh quay quanh Trái đất: Lực hấp dẫn giữa Trái đất và vệ tinh cung cấp lực hướng tâm để vệ tinh duy trì quỹ đạo tròn.
- Con lắc đơn: Khi con lắc di chuyển theo cung tròn, lực căng dây chính là lực hướng tâm.
Ví Dụ Tính Toán Lực Hướng Tâm
Dưới đây là một số ví dụ về cách tính lực hướng tâm trong các tình huống khác nhau:
- Một ô tô có khối lượng 1000 kg di chuyển với vận tốc 20 m/s trên một đường cong có bán kính 50 m. Tính lực hướng tâm tác dụng lên xe.
- Một vệ tinh có khối lượng 500 kg di chuyển trên quỹ đạo cách Trái đất 300 km với vận tốc 7,8 km/s. Tính lực hướng tâm giữ vệ tinh trên quỹ đạo.

Bài Tập Về Lực Hướng Tâm
Bài Tập Trắc Nghiệm
- Lực hướng tâm phụ thuộc vào yếu tố nào sau đây?
- a) Khối lượng của vật
- b) Bán kính của quỹ đạo
- c) Vận tốc của vật
- d) Cả ba yếu tố trên
- Trong trường hợp nào sau đây lực hướng tâm là lớn nhất?
- a) Vật có khối lượng nhỏ, vận tốc lớn, bán kính quỹ đạo nhỏ
- b) Vật có khối lượng lớn, vận tốc nhỏ, bán kính quỹ đạo lớn
- c) Vật có khối lượng lớn, vận tốc lớn, bán kính quỹ đạo nhỏ
- d) Vật có khối lượng nhỏ, vận tốc nhỏ, bán kính quỹ đạo lớn
Bài Tập Tự Luận
- Giải thích tại sao lực hướng tâm là cần thiết để giữ một vật di chuyển theo đường cong.
- Tính lực hướng tâm trong một bài toán cụ thể mà bạn chọn.
Ứng Dụng Của Lực Hướng Tâm
Lực hướng tâm xuất hiện trong nhiều tình huống trong cuộc sống hàng ngày và kỹ thuật, chẳng hạn như:
- Xe ô tô di chuyển trên đường cong: Khi một xe ô tô quay vòng, lực ma sát giữa bánh xe và mặt đường đóng vai trò như lực hướng tâm.
- Vệ tinh quay quanh Trái đất: Lực hấp dẫn giữa Trái đất và vệ tinh cung cấp lực hướng tâm để vệ tinh duy trì quỹ đạo tròn.
- Con lắc đơn: Khi con lắc di chuyển theo cung tròn, lực căng dây chính là lực hướng tâm.

Ví Dụ Tính Toán Lực Hướng Tâm
Dưới đây là một số ví dụ về cách tính lực hướng tâm trong các tình huống khác nhau:
- Một ô tô có khối lượng 1000 kg di chuyển với vận tốc 20 m/s trên một đường cong có bán kính 50 m. Tính lực hướng tâm tác dụng lên xe.
- Một vệ tinh có khối lượng 500 kg di chuyển trên quỹ đạo cách Trái đất 300 km với vận tốc 7,8 km/s. Tính lực hướng tâm giữ vệ tinh trên quỹ đạo.
Bài Tập Về Lực Hướng Tâm
Bài Tập Trắc Nghiệm
- Lực hướng tâm phụ thuộc vào yếu tố nào sau đây?
- a) Khối lượng của vật
- b) Bán kính của quỹ đạo
- c) Vận tốc của vật
- d) Cả ba yếu tố trên
- Trong trường hợp nào sau đây lực hướng tâm là lớn nhất?
- a) Vật có khối lượng nhỏ, vận tốc lớn, bán kính quỹ đạo nhỏ
- b) Vật có khối lượng lớn, vận tốc nhỏ, bán kính quỹ đạo lớn
- c) Vật có khối lượng lớn, vận tốc lớn, bán kính quỹ đạo nhỏ
- d) Vật có khối lượng nhỏ, vận tốc nhỏ, bán kính quỹ đạo lớn
Bài Tập Tự Luận
- Giải thích tại sao lực hướng tâm là cần thiết để giữ một vật di chuyển theo đường cong.
- Tính lực hướng tâm trong một bài toán cụ thể mà bạn chọn.
Ví Dụ Tính Toán Lực Hướng Tâm
Dưới đây là một số ví dụ về cách tính lực hướng tâm trong các tình huống khác nhau:
- Một ô tô có khối lượng 1000 kg di chuyển với vận tốc 20 m/s trên một đường cong có bán kính 50 m. Tính lực hướng tâm tác dụng lên xe.
- Một vệ tinh có khối lượng 500 kg di chuyển trên quỹ đạo cách Trái đất 300 km với vận tốc 7,8 km/s. Tính lực hướng tâm giữ vệ tinh trên quỹ đạo.
Bài Tập Về Lực Hướng Tâm
Bài Tập Trắc Nghiệm
- Lực hướng tâm phụ thuộc vào yếu tố nào sau đây?
- a) Khối lượng của vật
- b) Bán kính của quỹ đạo
- c) Vận tốc của vật
- d) Cả ba yếu tố trên
- Trong trường hợp nào sau đây lực hướng tâm là lớn nhất?
- a) Vật có khối lượng nhỏ, vận tốc lớn, bán kính quỹ đạo nhỏ
- b) Vật có khối lượng lớn, vận tốc nhỏ, bán kính quỹ đạo lớn
- c) Vật có khối lượng lớn, vận tốc lớn, bán kính quỹ đạo nhỏ
- d) Vật có khối lượng nhỏ, vận tốc nhỏ, bán kính quỹ đạo lớn
Bài Tập Tự Luận
- Giải thích tại sao lực hướng tâm là cần thiết để giữ một vật di chuyển theo đường cong.
- Tính lực hướng tâm trong một bài toán cụ thể mà bạn chọn.
Bài Tập Về Lực Hướng Tâm
Bài Tập Trắc Nghiệm
- Lực hướng tâm phụ thuộc vào yếu tố nào sau đây?
- a) Khối lượng của vật
- b) Bán kính của quỹ đạo
- c) Vận tốc của vật
- d) Cả ba yếu tố trên
- Trong trường hợp nào sau đây lực hướng tâm là lớn nhất?
- a) Vật có khối lượng nhỏ, vận tốc lớn, bán kính quỹ đạo nhỏ
- b) Vật có khối lượng lớn, vận tốc nhỏ, bán kính quỹ đạo lớn
- c) Vật có khối lượng lớn, vận tốc lớn, bán kính quỹ đạo nhỏ
- d) Vật có khối lượng nhỏ, vận tốc nhỏ, bán kính quỹ đạo lớn
Bài Tập Tự Luận
- Giải thích tại sao lực hướng tâm là cần thiết để giữ một vật di chuyển theo đường cong.
- Tính lực hướng tâm trong một bài toán cụ thể mà bạn chọn.
Giới Thiệu Chung
Lực hướng tâm là một khái niệm cơ bản trong vật lý, đặc biệt quan trọng đối với các hiện tượng liên quan đến chuyển động tròn đều. Lực này là lực giữ cho một vật thể di chuyển theo một quỹ đạo tròn, luôn hướng về tâm của quỹ đạo đó. Bất kỳ vật nào chuyển động trên quỹ đạo tròn đều chịu tác động của lực hướng tâm, từ các hạt nhỏ bé cho đến các hành tinh khổng lồ trong hệ mặt trời.
Trong công thức vật lý, lực hướng tâm được biểu diễn bởi phương trình:
\( F_{ht} = \frac{m \cdot v^2}{R} \)
Trong đó:
- Fht: Lực hướng tâm (N)
- m: Khối lượng của vật thể (kg)
- v: Vận tốc của vật thể (m/s)
- R: Bán kính quỹ đạo (m)
Với những ứng dụng thực tế rộng rãi, từ việc thiết kế máy móc đến sự hiểu biết về chuyển động của các thiên thể, lực hướng tâm đóng vai trò then chốt trong nhiều lĩnh vực khoa học và kỹ thuật.
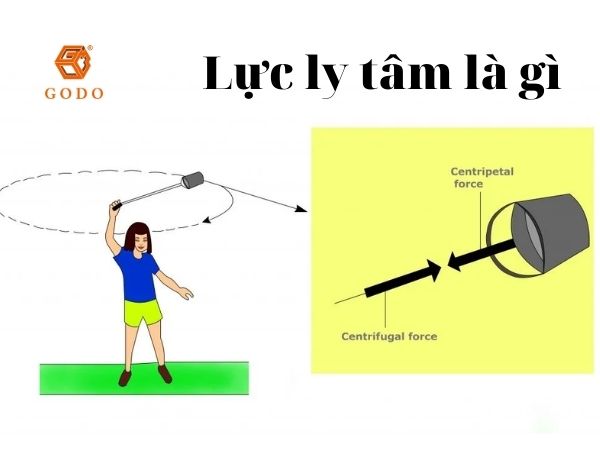
So Sánh Lực Hướng Tâm và Lực Ly Tâm
Lực hướng tâm và lực ly tâm là hai khái niệm thường xuyên được nhắc đến khi nghiên cứu về chuyển động tròn trong vật lý. Mặc dù có tên gọi gần giống nhau, nhưng chúng có bản chất và vai trò khác nhau. Dưới đây là bảng so sánh chi tiết giữa lực hướng tâm và lực ly tâm:
| Tiêu chí | Lực Hướng Tâm | Lực Ly Tâm |
|---|---|---|
| Định nghĩa | Lực hướng tâm là lực tác dụng vào vật thể chuyển động theo quỹ đạo tròn, hướng vào tâm của quỹ đạo. | Lực ly tâm là lực xuất hiện trong hệ quy chiếu quay, có xu hướng kéo vật thể ra xa khỏi tâm của quỹ đạo tròn. |
| Hướng tác dụng | Hướng vào tâm của quỹ đạo tròn. | Hướng ra xa tâm của quỹ đạo tròn. |
| Bản chất | Là lực thực, có thể do các lực khác như lực ma sát, lực hấp dẫn hoặc lực đàn hồi tạo ra. | Là lực quán tính, không có tác dụng thực sự mà chỉ là cảm nhận từ người quan sát trong hệ quy chiếu quay. |
| Công thức tính | \( F = \frac{mv^2}{r} \) | \( F = -\frac{mv^2}{r} \) |
| Ví dụ | Quả bóng buộc dây quay quanh trục, lực căng dây đóng vai trò là lực hướng tâm. | Người ngồi trong xe khi xe quay vòng sẽ cảm thấy bị đẩy ra phía ngoài của khúc cua. |
Sự khác biệt giữa lực hướng tâm và lực ly tâm không chỉ nằm ở hướng tác dụng mà còn ở bản chất của chúng. Việc hiểu rõ hai lực này giúp chúng ta nắm bắt tốt hơn các hiện tượng vật lý liên quan đến chuyển động tròn và áp dụng chúng vào thực tế một cách hiệu quả.