Momen lực được xác định bằng công thức: Hướng dẫn toàn diện và ứng dụng thực tế

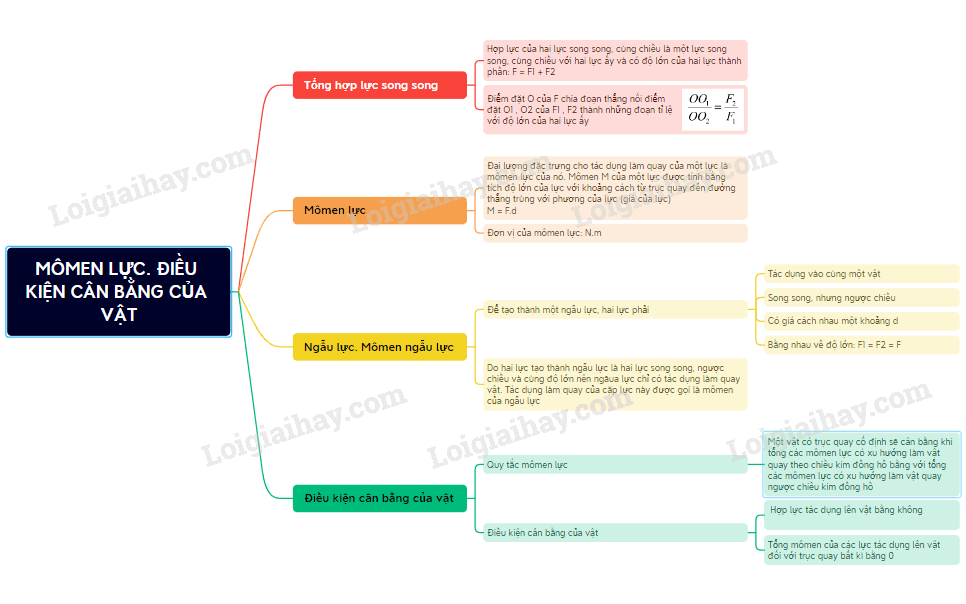
Momen lực là một khái niệm cơ bản trong vật lý và kỹ thuật cơ khí, thể hiện khả năng của một lực làm cho vật thể quay quanh một trục. Momen lực được xác định bằng công thức:

$$ M = F \cdot d $$

Trong đó:

• M: Momen lực (đơn vị: Newton-mét, N.m).
• F: Lực tác dụng (đơn vị: Newton, N).
• d: Cánh tay đòn, tức là khoảng cách từ điểm tác dụng lực đến trục quay (đơn vị: mét, m).

Các Quy Tắc Về Momen Lực

Quy tắc cơ bản về momen lực là nguyên tắc cân bằng của vật rắn có trục quay cố định. Để một vật ở trạng thái cân bằng, tổng các momen lực làm vật quay theo chiều kim đồng hồ phải bằng tổng các momen lực làm vật quay ngược chiều kim đồng hồ:

$$ M_1 = M_2 $$

Hoặc:

$$ F_1 \cdot d_1 = F_2 \cdot d_2 $$

Ứng Dụng Thực Tế

Momen lực có nhiều ứng dụng trong thực tế, đặc biệt trong các lĩnh vực như:

• Kỹ thuật cơ khí: Trong việc thiết kế và sử dụng các máy móc, momen lực đóng vai trò quan trọng trong truyền động lực và điều khiển chuyển động.
• Kỹ thuật xây dựng: Ứng dụng trong việc đảm bảo sự ổn định của các kết cấu, như cầu, nhà cao tầng.
• Đời sống hàng ngày: Sử dụng để mở cửa bằng tay nắm, hoặc trong các dụng cụ như cờ lê.

Ví Dụ Về Tính Toán Momen Lực

Giả sử một người tác dụng lực 100 N lên một cánh tay đòn dài 0.5 m. Khi đó, momen lực sẽ được tính như sau:

$$ M = 100 \, N \times 0.5 \, m = 50 \, N.m $$

Ví dụ này cho thấy cách tính toán momen lực dựa trên lực tác dụng và chiều dài cánh tay đòn, giúp hiểu rõ hơn về tầm quan trọng của momen lực trong các tình huống thực tế.

Một Số Khái Niệm Liên Quan

• Momen xoắn: Là một dạng đặc biệt của momen lực, thường được sử dụng để mô tả khả năng của động cơ trong việc quay các bánh răng hoặc trục.
• Momen ngẫu lực: Là hệ hai lực song song ngược chiều nhau tác dụng vào một vật thể, tạo ra chuyển động quay.

Momen lực là một phần không thể thiếu trong việc nghiên cứu và ứng dụng trong khoa học kỹ thuật, đóng góp vào nhiều giải pháp và cải tiến trong các ngành công nghiệp và đời sống.

Momen lực là một khái niệm quan trọng trong vật lý học, đặc biệt liên quan đến chuyển động quay. Nó mô tả hiệu ứng của một lực khi tác động lên một vật thể có trục quay, tạo ra xu hướng làm vật thể quay quanh trục đó.

Momen lực được xác định bằng tích của lực tác dụng lên vật và khoảng cách từ trục quay đến điểm đặt của lực. Công thức tính momen lực được viết như sau:

\( M = F \times d \)

• M: Momen lực, đơn vị là Newton-mét (N.m).
• F: Lực tác dụng, đơn vị là Newton (N).
• d: Khoảng cách từ trục quay đến điểm đặt của lực, đơn vị là mét (m).

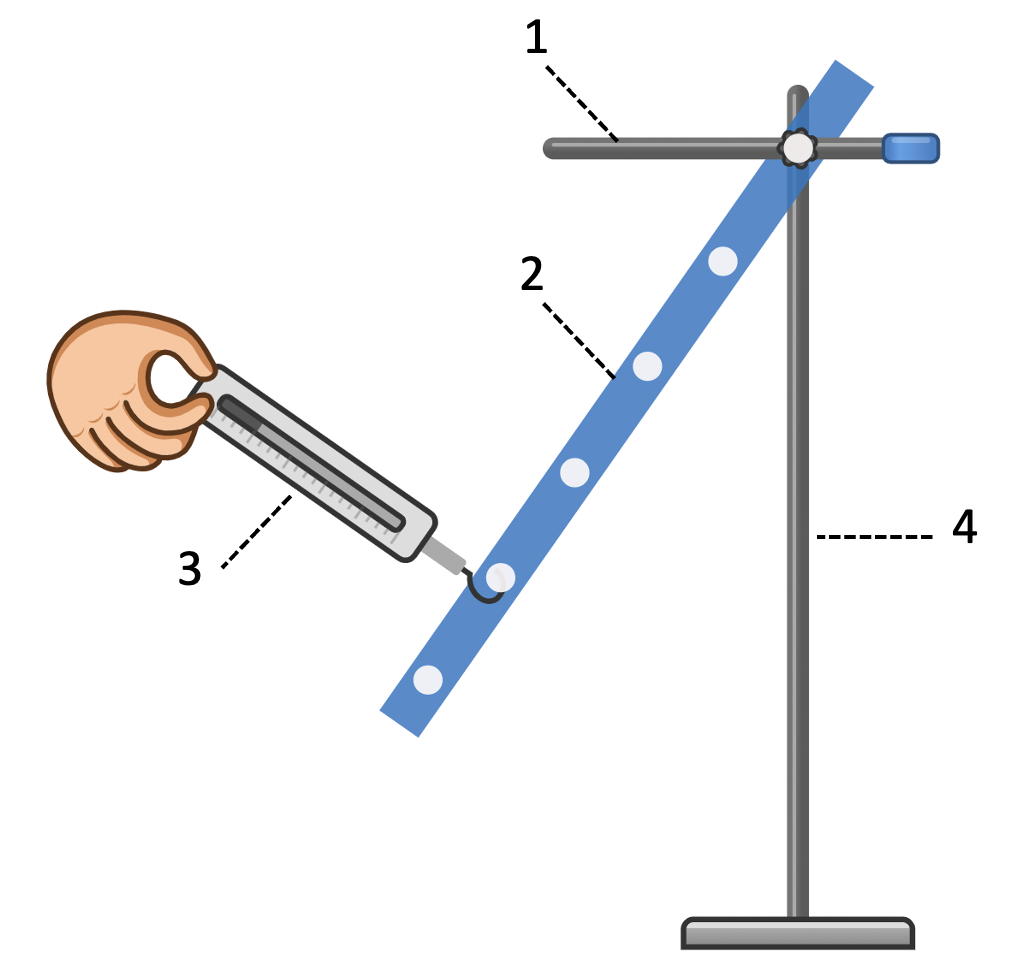
Ví dụ, khi bạn sử dụng một cờ lê để vặn ốc, lực mà bạn áp dụng lên cờ lê và khoảng cách từ tay bạn đến trục của ốc sẽ tạo ra momen lực. Nếu bạn tăng lực hoặc sử dụng một cờ lê dài hơn, momen lực sẽ tăng, giúp bạn dễ dàng hơn trong việc vặn ốc.

Momen lực không chỉ phụ thuộc vào độ lớn của lực mà còn phụ thuộc vào khoảng cách và góc giữa lực và cánh tay đòn. Khi lực tác động không vuông góc với cánh tay đòn, chỉ thành phần vuông góc của lực mới tham gia vào việc tạo momen lực.

Công thức tính momen lực được sử dụng để xác định mức độ quay của một vật thể khi có lực tác động lên nó. Công thức cơ bản của momen lực là:

\( M = F \times d \)

Trong đó:

• M: Momen lực, đơn vị là Newton-mét (N.m).
• F: Lực tác dụng lên vật, đơn vị là Newton (N).
• d: Khoảng cách vuông góc từ trục quay đến điểm đặt lực, đơn vị là mét (m).

Để tính momen lực chính xác, cần chú ý rằng lực phải vuông góc với cánh tay đòn (khoảng cách từ trục quay đến điểm đặt lực). Nếu lực không vuông góc, ta cần tính toán thành phần vuông góc của lực:

\( M = F \times d \times \sin(\theta) \)

Trong đó:

• \(\theta\): Góc giữa hướng của lực và cánh tay đòn.
• \(\sin(\theta)\): Thành phần vuông góc của lực tác động.

Ví dụ: Nếu một lực 50 N tác động lên một cánh tay đòn dài 0,5 m và vuông góc với nó, momen lực tạo ra sẽ là:

\( M = 50 \, \text{N} \times 0.5 \, \text{m} = 25 \, \text{N.m} \)

Trong trường hợp lực không vuông góc, ví dụ góc giữa lực và cánh tay đòn là 30 độ, ta có:

\( M = 50 \, \text{N} \times 0.5 \, \text{m} \times \sin(30^\circ) = 12.5 \, \text{N.m} \)

Công thức tính momen lực là nền tảng quan trọng trong nhiều lĩnh vực như cơ khí, xây dựng và vật lý, giúp xác định hiệu quả lực tác dụng và đảm bảo sự an toàn và hiệu suất trong thiết kế và hoạt động của các hệ thống cơ học.

Quy tắc momen lực là nguyên tắc cơ bản trong cơ học, được sử dụng để xác định điều kiện cân bằng của một vật thể khi có các lực tác dụng lên nó. Để một vật thể duy trì trạng thái cân bằng, tổng các momen lực tác dụng lên vật phải bằng 0. Nói cách khác, momen lực quay theo chiều kim đồng hồ phải cân bằng với momen lực quay ngược chiều kim đồng hồ.

Quy tắc này có thể được biểu diễn dưới dạng phương trình:

\( \sum M_{\text{cw}} = \sum M_{\text{ccw}} \)

Trong đó:

• \(\sum M_{\text{cw}}:\) Tổng momen lực quay theo chiều kim đồng hồ.
• \(\sum M_{\text{ccw}}:\) Tổng momen lực quay ngược chiều kim đồng hồ.

Điều kiện cân bằng này được áp dụng trong nhiều tình huống thực tế, từ thiết kế cầu, nhà cửa, đến tính toán lực trong các hệ thống cơ khí. Để kiểm tra điều kiện cân bằng, ta có thể làm theo các bước sau:

1. Xác định các lực tác dụng lên vật và vị trí điểm đặt của chúng.
2. Tính momen lực do từng lực gây ra, sử dụng công thức \( M = F \times d \).
3. Xác định chiều quay của mỗi momen lực (theo hoặc ngược chiều kim đồng hồ).
4. Tính tổng momen lực theo mỗi chiều quay.
5. So sánh tổng momen lực theo chiều kim đồng hồ và ngược chiều kim đồng hồ.

Nếu tổng các momen lực theo hai chiều quay bằng nhau, vật thể đang ở trạng thái cân bằng và không có xu hướng quay. Nếu không, vật sẽ quay theo chiều có tổng momen lực lớn hơn.

Ví dụ, nếu một thanh đòn chịu tác dụng của hai lực ở hai đầu, để thanh này cân bằng, lực và cánh tay đòn của hai bên phải đáp ứng quy tắc:

\( F_1 \times d_1 = F_2 \times d_2 \)

Trong đó:

• \(F_1, F_2\): Các lực tác dụng tại hai đầu thanh đòn.
• \(d_1, d_2\): Khoảng cách từ các điểm đặt lực đến trục quay.

Quy tắc momen lực không chỉ quan trọng trong lý thuyết mà còn có ứng dụng rộng rãi trong thực tiễn, từ thiết kế kết cấu cho đến phân tích các hệ thống cơ khí phức tạp.

Momen lực có nhiều ứng dụng quan trọng trong cả kỹ thuật và đời sống hàng ngày. Hiểu và áp dụng đúng momen lực giúp tối ưu hóa các hệ thống cơ học, đảm bảo an toàn và hiệu quả trong công việc. Dưới đây là một số ứng dụng tiêu biểu:

4.1 Ứng dụng trong cơ khí

Trong kỹ thuật cơ khí, momen lực là yếu tố cốt lõi để thiết kế và vận hành các máy móc và thiết bị.

• Trục động cơ: Momen lực được tạo ra bởi động cơ giúp các trục quay và truyền động, đảm bảo máy móc hoạt động mượt mà.
• Hệ thống cánh tay đòn: Các thiết bị như cần cẩu, cờ lê hay máy ép đều dựa vào momen lực để tạo ra lực đủ lớn để di chuyển hoặc nén vật liệu.
• Hộp số: Momen lực cũng quan trọng trong việc điều chỉnh tốc độ và lực quay trong các hệ thống truyền động cơ khí, như trong ô tô.

4.2 Ứng dụng trong xây dựng

Momen lực đóng vai trò quan trọng trong việc thiết kế và xây dựng các công trình đảm bảo độ bền và an toàn.

• Cầu và kết cấu thép: Khi thiết kế cầu, momen lực giúp xác định độ bền và khả năng chịu tải của các thành phần kết cấu.
• Cửa và bản lề: Momen lực được sử dụng để tính toán lực cần thiết để đóng mở cửa hoặc vận hành các thiết bị khác.

4.3 Ứng dụng trong đời sống hàng ngày

Momen lực không chỉ xuất hiện trong các hệ thống kỹ thuật mà còn được ứng dụng rộng rãi trong đời sống hàng ngày.

• Dụng cụ cầm tay: Khi sử dụng cờ lê để vặn ốc, momen lực giúp tạo ra lực xoắn lớn hơn với ít công sức hơn.
• Thiết bị gia dụng: Các thiết bị như máy giặt, máy xay sinh tố hay cửa gara đều dựa vào momen lực để vận hành các bộ phận quay.
• Thể thao: Trong các môn thể thao như bóng chày, gôn, việc tạo ra momen lực lớn từ cơ thể giúp tăng tốc độ và sức mạnh của cú đánh.

Momen lực là một khái niệm quen thuộc và cần thiết trong nhiều lĩnh vực. Hiểu rõ và ứng dụng đúng momen lực không chỉ giúp nâng cao hiệu suất làm việc mà còn đảm bảo an toàn và tối ưu hóa thiết kế trong các lĩnh vực khác nhau.

Momen lực là một phần của nhiều khái niệm khác trong cơ học, giúp hiểu sâu hơn về cách các lực và chuyển động tương tác với nhau. Dưới đây là một số khái niệm liên quan mật thiết đến momen lực:

5.1 Momen quán tính

Momen quán tính (ký hiệu \(I\)) là đại lượng đo lường mức độ chống lại sự thay đổi của chuyển động quay của một vật thể. Nó phụ thuộc vào khối lượng của vật và khoảng cách từ trục quay đến các phần tử khối lượng. Công thức tính momen quán tính cho một vật rắn đối với trục quay:

\( I = \sum m_i \times r_i^2 \)

Trong đó:

• \(m_i\): Khối lượng của phần tử thứ \(i\).
• \(r_i\): Khoảng cách từ phần tử đó đến trục quay.

5.2 Lực quay và mômen xoắn

Lực quay hay mômen xoắn (\(T\)) là khái niệm tương tự như momen lực, nhưng nó chủ yếu được sử dụng trong ngữ cảnh của động cơ và các hệ thống cơ học quay. Mômen xoắn có thể được hiểu là một momen lực gây ra sự xoay tròn. Công thức tính mômen xoắn:

\( T = r \times F \)

Trong đó:

• \(r\): Bán kính hoặc khoảng cách từ trục quay đến điểm tác dụng của lực.
• \(F\): Lực tác dụng.

5.3 Công cơ học

Công cơ học là khái niệm dùng để đo lượng năng lượng được truyền khi lực tác động làm dịch chuyển vật. Khi xét trong ngữ cảnh momen lực, công cơ học có thể được tính khi một lực làm quay một vật quanh trục cố định:

\( W = M \times \theta \)

Trong đó:

• \(W\): Công cơ học, đơn vị là Joule (J).
• \(M\): Momen lực, đơn vị là Newton-mét (N.m).
• \(\theta\): Góc quay tính bằng radian.

5.4 Định luật bảo toàn momen động lượng

Định luật này phát biểu rằng nếu không có ngoại lực tác động lên một hệ vật, momen động lượng của hệ đó sẽ được bảo toàn. Điều này có nghĩa là tổng momen động lượng trước và sau khi có sự thay đổi (như va chạm) sẽ bằng nhau.

\( L = I \times \omega \)

Trong đó:

• \(L\): Momen động lượng.
• \(I\): Momen quán tính.
• \(\omega\): Vận tốc góc.

Các khái niệm này không chỉ hỗ trợ việc hiểu momen lực mà còn là nền tảng cho nhiều lĩnh vực trong cơ học và kỹ thuật.

Khi tính toán momen lực, một số lỗi phổ biến có thể xảy ra, dẫn đến kết quả không chính xác hoặc hiểu sai vấn đề. Dưới đây là một số lỗi thường gặp và cách khắc phục chi tiết:

6.1 Sai lệch trong xác định điểm đặt lực

Momen lực được tính dựa trên khoảng cách từ trục quay đến điểm đặt lực. Một lỗi phổ biến là xác định sai điểm đặt lực, dẫn đến giá trị momen không chính xác.

• Lỗi: Xác định điểm đặt lực không chính xác, có thể là do nhầm lẫn vị trí hoặc không xem xét lực tác động đồng thời lên nhiều điểm.
• Cách khắc phục: Xem xét kỹ lưỡng lực tác dụng và xác định chính xác điểm đặt lực bằng cách sử dụng sơ đồ hoặc phân tích vật lý rõ ràng.

6.2 Nhầm lẫn chiều của momen lực

Chiều của momen lực (theo hoặc ngược chiều kim đồng hồ) đóng vai trò quan trọng trong việc xác định tổng momen và điều kiện cân bằng. Sai sót trong việc xác định chiều có thể dẫn đến kết quả ngược lại.

• Lỗi: Nhầm lẫn chiều của momen lực, dẫn đến sai sót khi cộng hoặc trừ các momen lực.
• Cách khắc phục: Xác định chiều quay của mỗi lực bằng cách phân tích kỹ lưỡng và đánh dấu rõ ràng trên sơ đồ lực. Hãy nhớ rằng momen quay theo chiều kim đồng hồ và ngược chiều kim đồng hồ cần được cộng riêng lẻ trước khi so sánh.

6.3 Tính toán sai khoảng cách từ trục quay

Khoảng cách từ trục quay đến điểm tác dụng lực (cánh tay đòn) là yếu tố quyết định trong công thức tính momen lực. Việc xác định sai khoảng cách này sẽ ảnh hưởng trực tiếp đến kết quả.

• Lỗi: Tính toán sai khoảng cách do không đo lường chính xác hoặc sử dụng giá trị không hợp lý.
• Cách khắc phục: Sử dụng các công cụ đo lường chính xác và kiểm tra lại các số liệu đã tính toán. Khi có các hình học phức tạp, hãy đảm bảo rằng bạn đã tính đến tất cả các yếu tố ảnh hưởng đến khoảng cách.

6.4 Bỏ qua lực hoặc momen phụ

Khi tính toán momen lực trong một hệ thống có nhiều lực tác động, việc bỏ sót các lực hoặc momen phụ có thể dẫn đến sai lệch nghiêm trọng.

• Lỗi: Không tính đến các lực nhỏ hoặc momen phụ, đặc biệt là trong các hệ thống phức tạp.
• Cách khắc phục: Phân tích toàn diện các lực tác dụng lên vật, bao gồm cả các lực phụ có thể bị bỏ qua. Đảm bảo rằng tất cả các lực đều được tính đến trong bài toán tổng quát.

6.5 Không sử dụng đơn vị đúng

Đơn vị của các đại lượng như lực (Newton), khoảng cách (mét), và momen lực (Newton-mét) phải được sử dụng nhất quán. Việc sử dụng đơn vị không đúng hoặc không đồng nhất có thể dẫn đến kết quả không chính xác.

• Lỗi: Sử dụng sai đơn vị hoặc không chuyển đổi đúng các đơn vị khi cần.
• Cách khắc phục: Kiểm tra kỹ các đơn vị trước khi bắt đầu tính toán. Sử dụng công cụ chuyển đổi đơn vị nếu cần thiết để đảm bảo sự nhất quán trong quá trình tính toán.

Việc nhận diện và khắc phục các lỗi thường gặp trong quá trình tính momen lực không chỉ giúp nâng cao độ chính xác mà còn tránh được những sai lầm nghiêm trọng trong thiết kế và ứng dụng thực tiễn.

Dưới đây là một số câu hỏi thường gặp liên quan đến momen lực, giúp bạn hiểu rõ hơn về khái niệm này và cách áp dụng trong thực tiễn.

7.1 Momen lực có phải luôn lớn hơn khi lực tác dụng ở khoảng cách xa hơn trục quay?

Đúng, momen lực tăng lên khi khoảng cách từ trục quay đến điểm đặt lực (cánh tay đòn) tăng lên. Điều này là do momen lực được tính bằng tích của lực và khoảng cách, do đó khi khoảng cách tăng, giá trị momen lực cũng tăng, với điều kiện lực tác dụng không thay đổi.

7.2 Momen lực có thể âm không?

Có, momen lực có thể âm nếu lực tác dụng làm quay vật theo chiều ngược chiều kim đồng hồ. Giá trị âm ở đây chỉ biểu thị chiều quay, không phải giá trị tuyệt đối của momen.

7.3 Momen lực và mômen quán tính có giống nhau không?

Không, momen lực và mômen quán tính là hai khái niệm khác nhau. Momen lực đo lường sự quay của vật dưới tác dụng của lực, trong khi mômen quán tính đo lường sự chống lại sự thay đổi chuyển động quay của vật. Mômen quán tính phụ thuộc vào khối lượng và hình dạng của vật.

7.4 Làm thế nào để tăng momen lực mà không tăng lực tác dụng?

Cách hiệu quả nhất để tăng momen lực mà không thay đổi lực tác dụng là tăng khoảng cách từ trục quay đến điểm đặt lực (tức là tăng chiều dài cánh tay đòn). Điều này giúp tăng cường hiệu quả của lực mà không cần phải tăng lực thực tế.

7.5 Momen lực có phụ thuộc vào hướng của lực tác dụng không?

Có, momen lực phụ thuộc vào hướng của lực tác dụng. Lực tác dụng phải có thành phần vuông góc với cánh tay đòn để tạo ra momen lực hiệu quả nhất. Nếu lực tác dụng theo hướng song song với cánh tay đòn, momen lực sẽ bằng 0 vì không có thành phần lực vuông góc.

Những câu hỏi trên đây bao quát một số khía cạnh quan trọng của momen lực, giúp làm rõ những thắc mắc thường gặp khi tìm hiểu về chủ đề này.